二叉树的基本操作

 图6所示的二叉树中，每个结点含一个字符，其非终端结点都是运算符，终端结点都是操作数。请编写程序，实现对该二叉树的基本操作。具体操作如表2所示。请自行编写主程序对各方法进行测试。

 

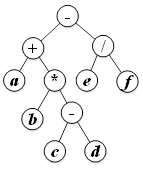
图6 一棵二叉树T

（1）按先序序列，建立二叉链表：编写程序，接收T的先序遍历序列string，根据string，建立T的二叉链表：btnode *creatTree(char *string): 其中，btnode为二叉链表的结点结构；string为T的先序遍历序列。

在输入的先序序列字符串string中，我们使用#来代替为NULL的树结点，如上图中a的左孩子和右孩子就用#代表，按照这个规则，先序遍历上图的树得到的string就为：

-+a##*b##-c##d##/e##f##

　　这也是我们创建树时要传递的字符串。

二叉树我们除了有存储当前树结点值的val外，还需要两个指针left,right，分别指向该根节点的左孩子和右孩子。这里我们用的是孩子双亲表示法，也可以使用其他的表示方法，如孩子兄弟表示法，left指向当前树结点的孩子结点，right指向当前树结点右边的兄弟结点。

树结点结构体为：

typedef struct btnode{
	char val;
	struct btnode *left,*right;
}bttree;

　　接着是按照输入的字符串创建二叉链表，因为每一个树结点都需要存储一个运算符或者运算数，所以使用全局变量index作为string移动的下标。传入的字符串是按照先序序列输入的，我们创建树的时候也按照先序创建。对于字符串中每一个不为#号的字符，开辟树结点空间，存储string[index]字符，同时递归其左子树和右子树，每次递归的时候都需要令index递增。

递归结束的条件是遇到的#字符，简单模拟一下创建树的过程：

输入字符串为：-+a##*b##-c##d##/e##f##

1，遇到-，开辟树结点，存储-，递归创建其左子树和右子树

2，进入创建其左子树的过程中

3，遇到+，开辟树结点，存储+，递归创建其左子树和右子树

4，遇到a，开辟树结点，存储a，递归创建其左子树和右子树

5，遇到#，故a的左子树为NULL，进入创建a的右子树的递归中

6，遇到#，故a的右子树为NULL，进入创建+的右子树递归中

7，遇到*，开辟树结点，存储*，递归创建其左子树和右子树

......

等等

最后返回最开始的根结点，即-的树结点root

如上，就可以创建出一棵按照输入的先序序列字符串顺序的二叉树

创建过程代码为：

#define LEN sizeof(btnode)
int index=0;
btnode* creatTree(char* string){
	char temp=*(string+index++);
	btnode* root=NULL;
	if(temp=='#'){
		root=NULL;
	}else{
		root=(btnode*)malloc(LEN);
		root->val=temp;
		root->left=creatTree(string);
		root->right=creatTree(string);
	}
	return root;
}

　　

（2）二叉树遍历：编写程序，对T进行先序遍历、中序遍历、后序遍历

void preorder(btnode *T): 先序遍历T，输出其先序序列

void inorder(btnode *T): 中序遍历T，输出其中序序列

void postorder(btnode *T) : 后序遍历T，输出其后序序列

先序遍历，中序遍历，后续遍历，使用递归实现的话，思路上是一致的。

从先序遍历上说，想要输出一棵二叉树的先序序列，我们需要知道先序序列的含义，即先输出根节点，输出左子树，再输出右子树。对于其左子树，也是先输出左子树的根节点，左子树的左子树，再输出左子树的右子树。递归点出现，我们只需要按照这个规则递归即可，当当前树结点为空时，就不再继续递归该子树。当树根结点的右子树也递归结束后，就代表整棵树的先序遍历结束了。

先序遍历代码如下：（对于#因为其是NULL结点，我们就不再输出了）

void preorder(btnode* T){
	btnode* temp=T;
	if(temp==NULL){
//		printf("#");
		return ;
	}else{
		printf("%c",temp->val);
		preorder(temp->left);
		preorder(temp->right);
	}	
}

　　可以看到，输出的时候，也是按照刚才我们所说的规则输出，中序遍历和后序遍历跟其类似，只需要改变输出当前树结点值的位置即可。

中序遍历：

void inorder(btnode* T){
	btnode* temp=T;
	if(temp==NULL){
//		printf("#");
		return ;
	}else{
		inorder(temp->left);
		printf("%c",temp->val);
		inorder(temp->right);
	}	
}

　　

后序遍历：

void postorder(btnode* T){
	btnode* temp=T;
	if(temp==NULL){
//		printf("#");
		return ;
	}else{
		postorder(temp->left);
		postorder(temp->right);
		printf("%c",temp->val);
	}	
}

　　

（3）求二叉树的叶子数：编写程序，求T的叶子数

int countLeaf(btnode *T);

求二叉树的叶子数，我们也使用递归的方式，想要求得一棵树的叶子数量，即判断当前树结点是否为叶子节点，是的话叶子节点数目+1，否则递归计算其左子树和右子树上叶子数的和。

是用静态局部变量存储叶子数

int countLeaf(btnode* T){
	btnode* temp=T;
	static int count=0;
	if(temp&&temp->left==NULL&&temp->right==NULL){
		count++;
		return 0;
	}else{
		countLeaf(temp->left);
		countLeaf(temp->right);
	}
	return count;
}

　　

（4）求二叉树的深度：编写程序，求T的深度

int high(btnode *T)：编写程序，求T的深度

还是递归的思想，很多问题使用递归解决，就会变得很简单

想要求一棵树的深度，即求其左子树和右子树中，最大的深度+1，+1的原因即算上当前树结点的深度为1

int max(int a,int b){
	return a>b?a:b;
}
int high(btnode* T){
	btnode* temp=T;
	if(temp==NULL){
		return 0;
	}else{
		return max(high(temp->left)+1,high(temp->right)+1);
	}
}

　　

（5）输出带括号的中缀表达式：如果对T进行中序遍历，将得到一个中缀表达式，但该表达式没有小括号，无法体现运算的优先级。请编写程序，对二叉树T，输出其带小括号的中缀表达式。

void infixExpression(btnode *T);

可以发现，我们中序遍历二叉树时，结果为：

 而在树的结构中，很明显是c-d，但是在输出的结果表达式中却体现不出这一点，这道题的目的就是让我们添加括号体现优先级。

类似于逆波兰式中运算符优先级的判定，考虑什么情况下我们需要添加括号，实际上只有当前树结点的运算符优先级大于其左子树或右子树根节点的运算符优先级时，才需要添加括号。而什么时候当前树结点的运算符优先级大于其左子树或右子树的根节点运算符优先级，其实只有一种情况，即当前树结点为乘号或者除号，而左子树或右子树为减号或者加号，这时候才需要添加括号。即便左子树或右子树不是运算符，也在上述判断中不满足条件，也就是不添加括号。

使用check函数进行优先级判定

当根结点运算符优先级高于左子树或右子树根结点运算符时，返回true，添加括号

bool check(char a,char b){
	if((a=='+'||a=='-')&&(b=='*'||b=='/')){
        return true;
    }else{
        return false;
    }
}

　因为是在中序遍历的基础上添加括号，所以我们也在中序遍历代码的基础上进行修改

　代码为：

void infixExpression(btnode* T){
	btnode* temp=T;
	if(temp==NULL){
//		printf("#");
		return ;
	}else{
		if(temp->left){
			bool flag=check(temp->left->val,temp->val);
			if(flag){
				printf("(");
			}
			infixExpression(temp->left);
			if(flag){
				printf(")");
			}
		}
		printf("%c",temp->val);
		if(temp->right){
			bool flag=check(temp->right->val,temp->val);
			if(flag){
				printf("(");
			}
			infixExpression(temp->right);
			if(flag){
				printf(")");
			}
		}
	}	
}

　　判定每一个树结点与其左右孩子的根节点的优先级，满足条件时输出左括号，递归其左子树，递归结束后再输出右括号。其余过程与中序遍历差别不大。

完整代码为：

#include<stdio.h>
#include<stdlib.h>
#include<string.h>


typedef struct btnode{
	char val;
	struct btnode *left,*right;
}bttree;

#define LEN sizeof(btnode)
int max(int a,int b){
	return a>b?a:b;
}
void preorder(btnode* T){
	btnode* temp=T;
	if(temp==NULL){
//		printf("#");
		return ;
	}else{
		printf("%c",temp->val);
		preorder(temp->left);
		preorder(temp->right);
	}	
}

void inorder(btnode* T){
	btnode* temp=T;
	if(temp==NULL){
//		printf("#");
		return ;
	}else{
		inorder(temp->left);
		printf("%c",temp->val);
		inorder(temp->right);
	}	
}

void postorder(btnode* T){
	btnode* temp=T;
	if(temp==NULL){
//		printf("#");
		return ;
	}else{
		postorder(temp->left);
		postorder(temp->right);
		printf("%c",temp->val);
	}	
}

int countLeaf(btnode* T){
	btnode* temp=T;
	static int count=0;
	if(temp&&temp->left==NULL&&temp->right==NULL){
		count++;
		return 0;
	}else{
		countLeaf(temp->left);
		countLeaf(temp->right);
	}
	return count;
}

//求树的深度，即求左子树和右子树中的最大深度，出现递归点 
int high(btnode* T){
	btnode* temp=T;
	if(temp==NULL){
		return 0;
	}else{
		return max(high(temp->left)+1,high(temp->right)+1);
	}
}

bool check(char a,char b){
	if((a=='+'||a=='-')&&(b=='*'||b=='/')){
        return true;
    }else{
        return false;
    }
}

//输出带括号的中缀表达式，当根结点运算符优先级高于左子树或右子树根结点运算符时，相应左或右子树前就需要加括号
void infixExpression(btnode* T){
	btnode* temp=T;
	if(temp==NULL){
//		printf("#");
		return ;
	}else{
		if(temp->left){
			bool flag=check(temp->left->val,temp->val);
			if(flag){
				printf("(");
			}
			infixExpression(temp->left);
			if(flag){
				printf(")");
			}
		}
		printf("%c",temp->val);
		if(temp->right){
			bool flag=check(temp->right->val,temp->val);
			if(flag){
				printf("(");
			}
			infixExpression(temp->right);
			if(flag){
				printf(")");
			}
		}
	}	
}
int index=0;
btnode* creatTree(char* string){
	char temp=*(string+index++);
	btnode* root=NULL;
	if(temp=='#'){
		root=NULL;
	}else{
		root=(btnode*)malloc(LEN);
		root->val=temp;
		root->left=creatTree(string);
		root->right=creatTree(string);
	}
	return root;
}
int main(){
	btnode* root=creatTree("-+a##*b##-c##d##/e##f##");
	printf("输入字符串为：-+a##*b##-c##d##/e##f##
");
	printf("先序遍历结果为：");
	preorder(root);
	printf("
中序遍历结果为：");
	inorder(root);
	printf("
后序遍历结果为：");
	postorder(root);
	printf("
二叉树的叶子数为：%d
",countLeaf(root));
	printf("二叉树的深度为：%d
",high(root));
	printf("带括号的中缀表达式为：");
	infixExpression(root);
	free(root);
	return 0;
}

　　

在二叉树的操作中，递归是经常会用到也是很重要的思想，需要熟练掌握应用，以及举一反三。

以上