Before the Beginniing
本文为 Clouder 原创文章,原文链接为Click,转载时请将本段放在文章开头显眼处。如进行了二次创作,请明确标明。
由本人转载于博客园。
题意分析
Codeforces题目链接
给出一个 (n imes m) 的矩阵,给出两种操作:
- 将某一列整体向上移动一位。
- 修改某一个位置的值。
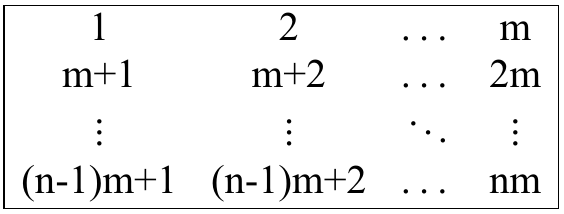
求最少要多少次操作,使得矩阵成为如下形式:
思路
很容易发现,每一列的操作都是独立的。
那么就一列列处理即可。
问题转化为如何求一列变为目标形式的最少操作次数。
而修改和平移是不冲突的,可以直接考虑先平移再修改。
暴力枚举法
于是得到一个很直观的思路,枚举向上移动多少次,再检查每一个数计算要修改多少次达到目标状态。
这样每列的复杂度是 (O(n^2)) 的,总复杂度显然不可接受。
计算位置法
考虑每列要修改多少次受什么影响。
在向上平移特定距离之后,如果平移后有位置刚好对应上,则不需要修改。
每个位置数确定之后,其能对应的位置也确定了,可以直接计算出在平移几格时的情况该位置不需要修改。
比如图中第一列,第二行如果有一个数 (1),可以直接通过计算得出其应当在的位置为第一行,于是在平移一格时的情况它不用修改,记录下来即可。
那么整体把矩阵扫一遍处理即可,时间复杂度 (O(nm)),可以通过。
解法
还是有一些细节的。
首先不能直接开 (nm) 大小的数组,会爆空间,这里使用了 vector 来处理。
而 (s[i]) 代表的是 向上平移 (i) 格时有多少个位置不需要修改。
那么操作步数可以通过平移格数和修改数计算出。
这里的数组 (s) 直接滚动优化掉一维,注意使用循环清空,就不会清空不使用的部分,而用 memset 会超时。
计算新位置建议自己画图手推一下,代个例子进去。
由于使用 vector,下标从 (0) 开始了,按个人习惯来吧。
代码
#include <cstdio>
#include <vector>
using namespace std;
inline int read()
{
static char c;
int r = 0;
for (c = getchar(); c > '9' || c < '0'; c = getchar());
for (; c >= '0' && c <= '9'; r = (r << 1) + (r << 3) + (c ^ 48), c = getchar());
return r;
}
const int maxn = 2e5 + 100;
int n, m;
vector<int> a[maxn];
int s[maxn];
int ans;
int main()
{
n = read();
m = read();
for (int i = 0; i < n; ++i)
for (int j = 0; j < m; ++j)
a[i].push_back(read());
int maxx = n * m;
for (int j = 0; j < m; ++j)
{
for (int i = 0; i < n; ++i)
s[i] = 0;
for (int i = 0; i < n; ++i)
{
if (a[i][j] > maxx || a[i][j] < j || ((a[i][j] - j - 1) % m) != 0)
continue;
int p = (a[i][j] - j - 1) / m;
if (i >= p)
s[i - p]++;
else
s[i + n - p]++;
}
int res = 1 << 30;
for (int i = 0; i < n; ++i)
if (n - s[i] + i < res)
res = n - s[i] + i;
ans += res;
}
printf("%d
", ans);
return 0;
}