今天又是例行考试的说。
话说我今天loj大凶且忌参加模拟赛,洛谷也好不到哪去,怕不是要爆零了QAQ。


T1:卡片游戏:

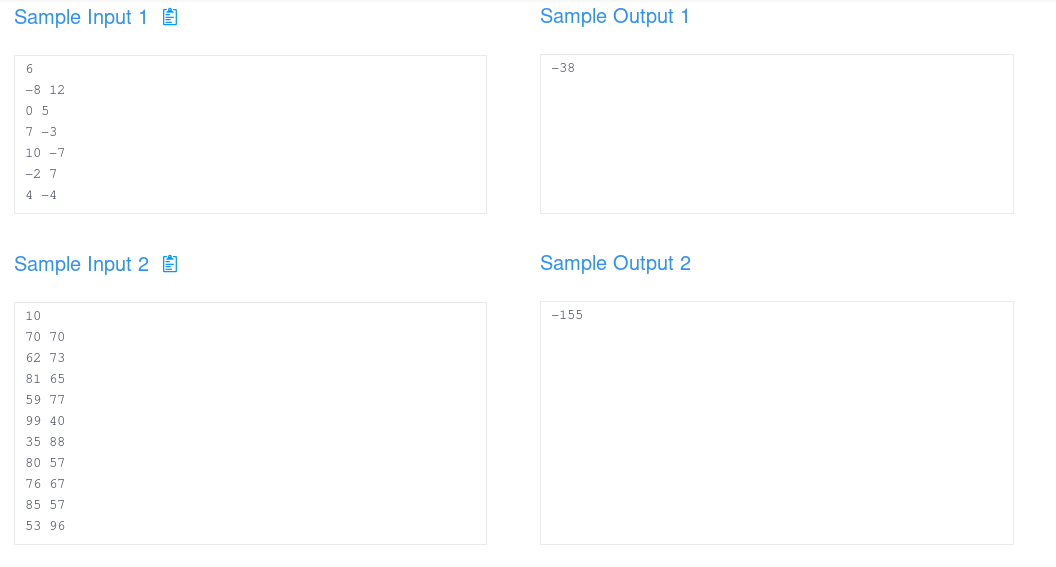

这题看到数据范围1e5,铁定不是费用流了。
这种东西显然不可能是dp,看看怎么贪心?
首先,我们如果给一张卡片负号,则一定去较大的那个值,正号则取较小的那个。
两边的差值是大小两值的和。
所以,我们先贪心地给负号,并把卡片放进一个堆里,如果堆已满且堆顶的数值和小于当前卡片的数值和,那么我们弹出堆顶,放入当前卡片。
考虑一正一负且负数的绝对值大的情况,也能通过。
写了拍了没啥问题,就这样了。
代码:

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<set> 6 #define debug cout 7 using namespace std; 8 const int maxn=1e5+1e2; 9 10 struct Node { 11 int mx,mi; 12 friend bool operator < (const Node &a,const Node &b) { 13 return a.mx + a.mi < b.mx + b.mi; 14 } 15 }ns[maxn]; 16 17 multiset<Node> heap; 18 19 int main() { 20 static int n,lim,ans; 21 scanf("%d",&n) , lim = n >> 1; 22 for(int i=1;i<=n;i++) { 23 scanf("%d%d",&ns[i].mx,&ns[i].mi); 24 if( ns[i].mx < ns[i].mi ) 25 swap(ns[i].mx,ns[i].mi); 26 } 27 for(int i=1;i<=n;i++) { 28 if( heap.size() < lim ) { 29 heap.insert(ns[i]); 30 ans -= ns[i].mx; 31 } else if( *heap.begin() < ns[i] ) { 32 Node b = *heap.begin(); 33 heap.erase(heap.begin()); 34 ans += b.mx , ans += b.mi; 35 heap.insert(ns[i]); 36 ans -= ns[i].mx; 37 } else ans += ns[i].mi; 38 } 39 40 printf("%d ",ans); 41 42 return 0; 43 }
T2:nimgame:
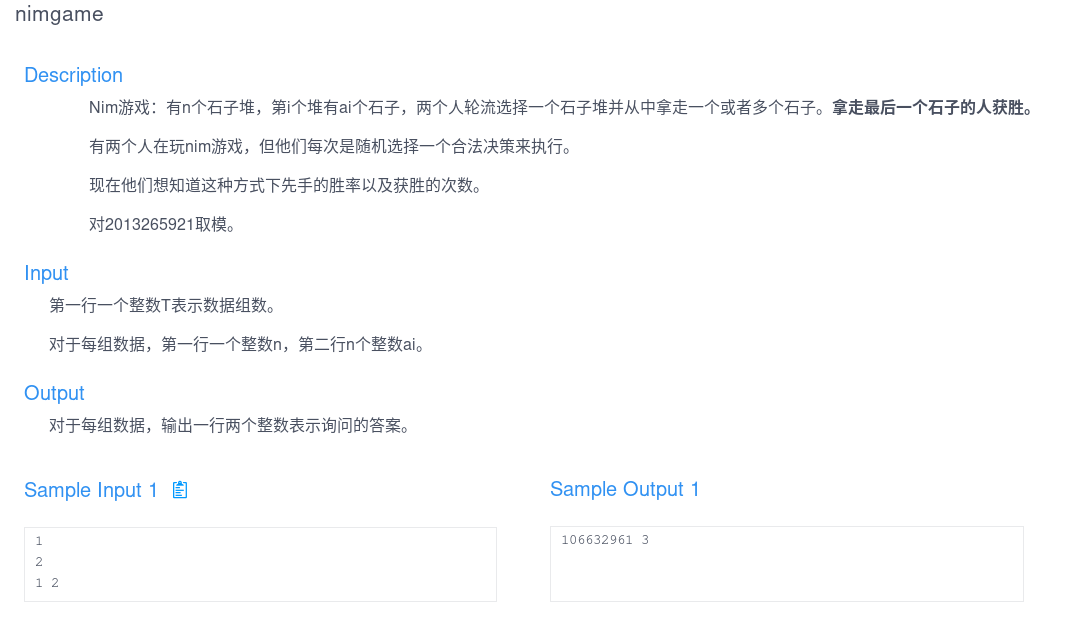

nim游戏?xor?随机方案?不可做不可做,敲了n!暴力走人。
然后爆零了...…
正解是NTT,首先第一问如果不是全1则一定为1/2(归纳法易证,有空再补,Fedora输入法反人类!),
第二问就是奇数次取完的方案数,如果我们算出k次取完每一个的数量,那么答案就是个卷积,指数生成函数启发式NTT即可。
爆零爆搜代码:

1 #pragma GCC optimize(3) 2 #pragma GCC optimize("-funsafe-loop-optimizations") 3 #pragma GCC optimize("-funroll-loops") 4 #pragma GCC optimize("-fwhole-program") 5 #pragma GCC target("mmx") 6 #include<cstdio> 7 #define lli long long int 8 #define debug cout 9 using namespace std; 10 const int maxn=1e2+1e1; 11 const int mod = 2013265921; 12 13 int in[maxn],n; 14 struct Node { 15 lli exp; 16 int way,full; 17 }; 18 inline lli rev(int base) { 19 int tme = mod - 2; 20 lli ret = 1 , now = base; 21 while( tme ) { 22 if( tme & 1 ) ret = ret * now % mod; 23 now = now * now % mod; 24 tme >>= 1; 25 } 26 return ret; 27 } 28 29 inline bool empty() { 30 for(int i=1;i<=n;i++) 31 if( in[i] ) return 0; 32 return 1; 33 } 34 Node dfs() { 35 if( empty() ) 36 return (Node){0,0,1}; 37 Node ret = (Node){0,0,0}; 38 int ways = 0 , full = 0; 39 for(int i=1;i<=n;i++) 40 if( in[i] ) 41 for(int j=1;j<=in[i];j++) { 42 in[i] -= j; 43 ++ways; 44 Node nxt = dfs(); 45 ret.exp += ( 1 - nxt.exp + mod ) % mod , ret.exp %= mod , ret.way += nxt.way , full += nxt.full; 46 in[i] += j; 47 } 48 ret.exp = ret.exp * rev(ways) % mod; 49 ret.way = full - ret.way; 50 ret.full = full; 51 return ret; 52 } 53 54 int main() { 55 static int T; 56 scanf("%d",&T); 57 while( T--) { 58 scanf("%d",&n); 59 for(int i=1;i<=n;i++) 60 scanf("%d",in+i); 61 Node ans = dfs(); 62 printf("%lld %d ",ans.exp,ans.way); 63 } 64 return 0; 65 }
正解代码:

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<functional> 6 #include<vector> 7 #include<queue> 8 #define lli long long int 9 #define debug cout 10 using namespace std; 11 const int maxn=5e4+1e2,maxl=1<<17; 12 const int mod = 2013265921 , g = 31; 13 14 int len[maxn]; 15 lli fac[maxn],invfac[maxn]; 16 vector<lli> v[maxn]; 17 priority_queue<pair<int,int>,vector<pair<int,int> >,greater<pair<int,int> > > pq; 18 19 inline lli fastpow(lli base,int tme,int mod) { 20 lli ret = 1; 21 while( tme ) { 22 if( tme & 1 ) ret = ret * base % mod; 23 base = base * base % mod; 24 tme >>= 1; 25 } 26 return ret; 27 } 28 inline lli getinv(lli x) { 29 return fastpow(x,mod-2,mod); 30 } 31 inline lli c(int n,int m) { 32 return fac[n] * invfac[m] % mod * invfac[n-m] % mod; 33 } 34 35 inline int revbit(int x,int len) { 36 int ret = 0; 37 for(int t=1;t<len;t<<=1) 38 ret <<= 1 , ret |= x&1 , x >>= 1; 39 return ret; 40 } 41 inline void NTT(lli* dst,int n,int ope) { 42 for(int i=0,j;i<n;i++) { 43 j = revbit(i,n); 44 if( i < j ) swap(dst[i],dst[j]); 45 } 46 for(int len=2;len<=n;len<<=1) { 47 lli per = fastpow( g , mod / len , mod ); 48 if( !~ope ) per = getinv(per); 49 for(int st=0;st<n;st+=len) { 50 lli w = 1; 51 for(int pos=0;pos<len>>1;pos++) { 52 const lli x = dst[st+pos] , y = dst[st+pos+(len>>1)] * w % mod; 53 dst[st+pos] = ( x + y ) % mod , 54 dst[st+pos+(len>>1)] = ( x - y + mod ) % mod; 55 w = w * per % mod; 56 } 57 } 58 } 59 if( !~ope ) { 60 lli inv = getinv(n); 61 for(int i=0;i<n;i++) 62 dst[i] = dst[i] * inv % mod; 63 } 64 } 65 inline void mul(int x,int y) { // multi v[x] v[y] into v[x] and update len[x] 66 static lli a[maxl],b[maxl]; 67 int n = 1 , lx = len[x] , ly = len[y]; 68 while( n <= lx + ly ) n <<= 1; 69 memset(a,0,sizeof(lli)*(n+1)) , memset(b,0,sizeof(lli)*(n+1)); 70 for(int i=0;i<=lx;i++) a[i] = v[x][i]; 71 for(int i=0;i<=ly;i++) b[i] = v[y][i]; 72 NTT(a,n,1) , NTT(b,n,1); 73 for(int i=0;i<n;i++) 74 a[i] = a[i] * b[i] % mod; 75 NTT(a,n,-1); 76 n = len[x] + len[y]; 77 v[x].resize(n+1) , len[x] = n; 78 for(int i=0;i<=n;i++) 79 v[x][i] = a[i]; 80 } 81 82 inline void merge() { 83 while( pq.size() > 1 ) { 84 const int y = pq.top().second; pq.pop(); 85 const int x = pq.top().second; pq.pop(); 86 mul(x,y) , v[y].resize(0); 87 pq.push( make_pair(len[x],x) ); 88 } 89 } 90 inline void prefac(int x) { 91 *fac = 1; 92 for(int i=1;i<=x;i++) 93 fac[i] = fac[i-1] * i % mod; 94 invfac[x] = getinv(fac[x]); 95 for(int i=x-1;~i;i--) 96 invfac[i] = invfac[i+1] * ( i + 1 ) % mod; 97 } 98 inline void getans() { 99 int n , sum = 0 , exp = 1006632961; 100 lli ans = 0; 101 scanf("%d",&n); 102 for(int i=1;i<=n;i++) 103 scanf("%d",len+i) , sum += len[i]; 104 prefac(sum); 105 for(int i=1;i<=n;i++) { 106 v[i].resize(len[i]+1); 107 for(int j=1;j<=len[i];j++) 108 v[i][j] = c(len[i]-1,j-1) * invfac[j] % mod; 109 pq.push( make_pair(len[i],i) ); 110 } 111 merge(); 112 const int x = pq.top().second; pq.pop(); 113 for(int i=1;i<=len[x];i+=2) 114 ans += v[x][i] * fac[i] % mod , ans %= mod; 115 if( n == sum ) exp = n & 1; 116 printf("%d %lld ",exp,ans); 117 } 118 119 int main() { 120 static int t; 121 scanf("%d",&t); 122 while( t-- ) 123 getans(); 124 return 0; 125 }
T3:palindrome:
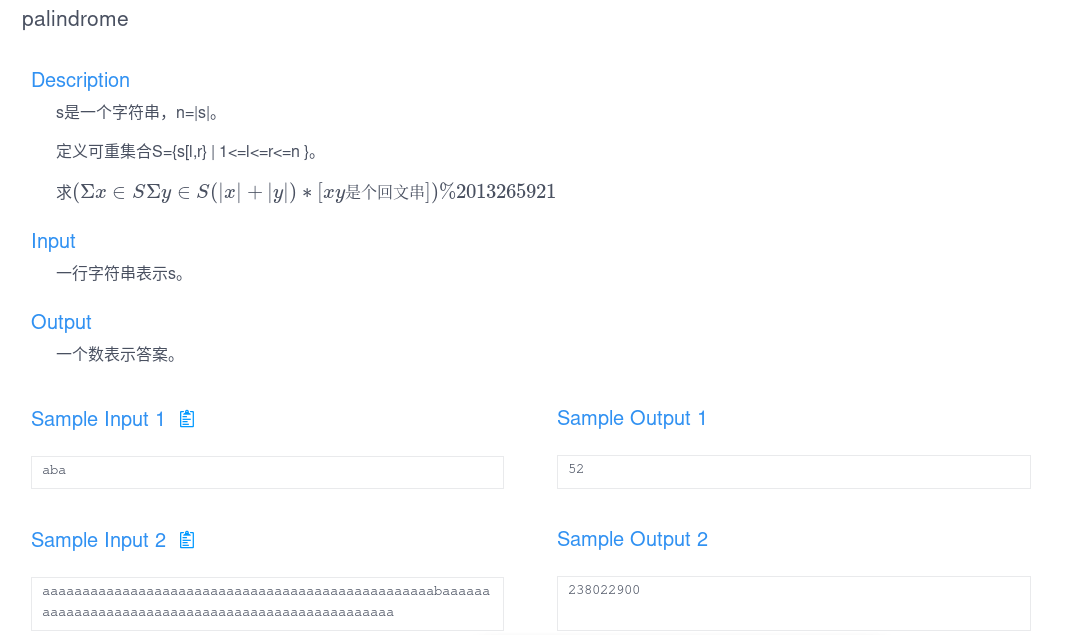

一开始想SAM乱搞发现会被abb坑掉(abb+a),然后交对排用的string的n^5暴力感觉不保险,于是写了一个30分的哈希。(后来发现string也能过...…)
正解暂时弃坑辣!
30分哈希代码:

1 #pragma GCC optimize(3) 2 #pragma GCC optimize("-funsafe-loop-optimizations") 3 #pragma GCC optimize("-funroll-loops") 4 #pragma GCC optimize("-fwhole-program") 5 #pragma GCC target("avx") 6 #include<cstdio> 7 #include<cstring> 8 #define ulli unsigned long long 9 using namespace std; 10 const int maxn=1e3+1e2; 11 const ulli base = 233; 12 const ulli mod = 2013265921; 13 14 char s[maxn]; 15 ulli in[maxn],hsh1[maxn],hsh2[maxn],pows[maxn],ans; 16 int n; 17 18 inline void inithsh() { 19 for(int i=1;i<=n;i++) 20 in[i] = s[i] - 'a' + 1; 21 for(int i=1;i<=n;i++) 22 hsh1[i] = hsh1[i-1] * base + in[i]; 23 for(int i=n;i;i--) 24 hsh2[i] = hsh2[i+1] * base + in[i]; 25 *pows = 1; 26 for(int i=1;i<=n;i++) 27 pows[i] = pows[i-1] * base; 28 } 29 inline ulli segment1(int st,int ed) { 30 --st; 31 return hsh1[ed] - hsh1[st] * pows[ed-st]; 32 } 33 inline ulli segment2(int st,int ed) { 34 ++ed; 35 return hsh2[st] - hsh2[ed] * pows[ed-st]; 36 } 37 inline ulli merge1(int sx,int tx,int sy,int ty) { 38 return segment1(sx,tx) * pows[ty-sy+1] + segment1(sy,ty); 39 } 40 inline ulli merge2(int sx,int tx,int sy,int ty) { 41 return segment2(sy,ty) * pows[tx-sx+1] + segment2(sx,tx); 42 } 43 inline bool judge(int sx,int tx,int sy,int ty) { 44 return merge1(sx,tx,sy,ty) == merge2(sx,tx,sy,ty); 45 } 46 47 int main() { 48 scanf("%s",s+1); 49 n = strlen(s+1); 50 inithsh(); 51 for(int sx=1;sx<=n;++sx) { 52 for(int tx=sx;tx<=n;++tx) 53 for(int sy=1;sy<=n;++sy) 54 for(int ty=sy;ty<=n;++ty) 55 if( judge(sx,tx,sy,ty) ) 56 ans += tx - sx + ty - sy + 2; 57 ans %= mod; 58 } 59 60 printf("%llu ",ans); 61 62 return 0; 63 }
最后上ranking,反正T2T3谁也不会就是了。