zoukankan      html  css  js  c++  java

  • 北京集训:20180326

    爆零蒟蒻今天终于滚粗了......
    也就是说，这是北京集训的最后一篇题解了。之后的比赛，我已经没有访问权限了。


    T1:


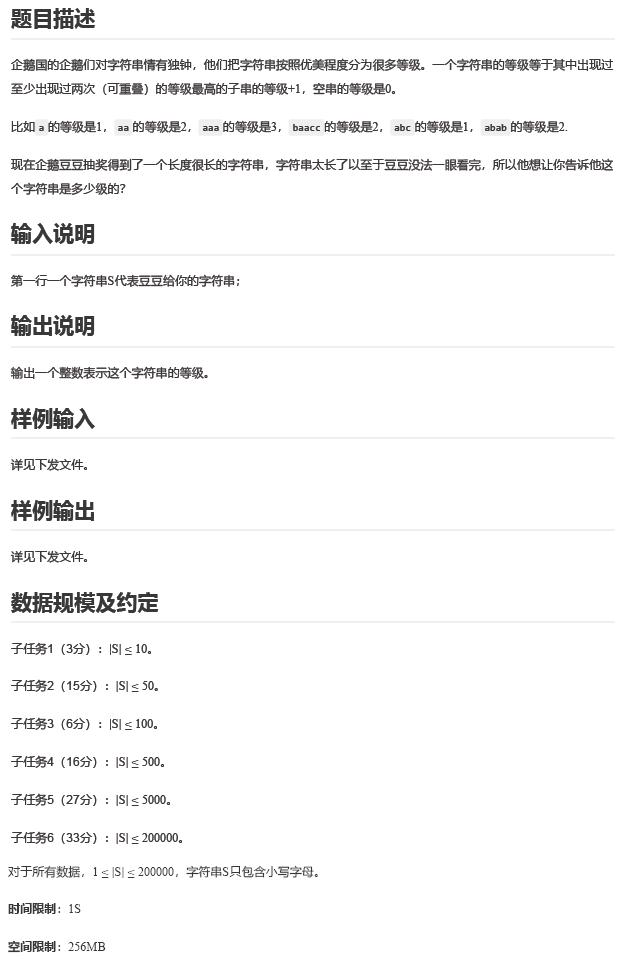
    考虑一个暴力做法:f[i][j]表示字符串区间[i,j]的最大等级。
    如果k级字符串[i,j]包含一个k-1级字符串s，且s没有达到[i,j]的首(或者尾)的话，我们去掉[i,j]的首(或者尾)，剩下的仍然是一个k级字符串。
    所以我们可以暴力dp，f[i][j]=max(f[i+1][j],f[i][j-1],max(f[substr])+1)。
    而后面的那个可以用后缀自动机枚举出现两次及以上的子串，总复杂度O(n^3)。
    显然这并不是正解(然而这对正解有很大的帮助)(要不然我也不会写他)。
    考虑我们这样增量(减量?不!)去掉首尾字符的过程，我们一定能保证一个k级字符串的首尾都是一个k-1级字符串。
    尾相同的子串有怎样的性质呢?他会出现在当前串的parent树的祖先上。
    于是我们可以用f[i]表示后缀自动机第i个节点及其祖先节点中，最大的等级，g[i]表示取到这个等级，所在的最短的节点。
    为什么这样做正确?因为对于结尾更靠后的串，我们不计算他的贡献也没有关系是吧，反正他能转移到的串的子串一定能由一个结尾更靠前的串转移到。
    转移显然用最短的节点转移最优。我们暴力找头上的那个串出现的位置，看看是否可行即可。
    这样我们get到了n^2暴力......
    考虑我们现在复杂度的瓶颈在哪里?维护right集合和查询的过程。于是我们可以反向建立主席树并进行启发式合并，复杂度O(nlogn)。
    (其实我感觉这东西时间和空间复杂度都是O(nlog^2n)的，只不过跑不满罢了)
    代码:

      1 #include<iostream>
  2 #include<cstdio>
  3 #include<cstring>
  4 #include<algorithm>
  5 #include<queue>
  6 #define debug cerr
  7 using namespace std;
  8 const int maxn=4e5+1e2;
  9 
 10 char in[maxn>>1];
 11 int li,ans=1;
 12 
 13 struct PersistentSegmentTree {
 14     static const int maxe = maxn * 25;
 15     int siz[maxe],lson[maxe],rson[maxe],cnt;
 16     
 17     inline void insert(int &pos,int l,int r,const int &tar) {
 18         if( !pos ) pos = ++cnt;
 19         siz[pos] = 1;
 20         if( l == r ) return;
 21         const int mid = ( l + r ) >> 1;
 22         if( tar <= mid ) return insert(lson[pos],l,mid,tar);
 23         else return insert(rson[pos],mid+1,r,tar);
 24     }
 25     inline int merge(int p1,int p2,int l,int r) {
 26         if( ! ( siz[p1] && siz[p2] ) ) return siz[p1] ? p1 : p2;
 27         int ret = ++cnt; siz[ret] = siz[p1] + siz[p2];
 28         if( l == r ) return ret;
 29         const int mid = ( l + r ) >> 1;
 30         lson[ret] = merge(lson[p1],lson[p2],l,mid);
 31         rson[ret] = merge(rson[p1],rson[p2],mid+1,r);
 32         return ret;
 33     }
 34     inline int query(int pos,int l,int r,const int &ll,const int &rr) {
 35         if( !pos ) return 0;
 36         if( ll <= l && r <= rr ) return siz[pos];
 37         const int mid = ( l + r ) >> 1;
 38         if( rr <= mid ) return query(lson[pos],l,mid,ll,rr);
 39         if( ll > mid ) return query(rson[pos],mid+1,r,ll,rr);
 40         return query(lson[pos],l,mid,ll,rr) + query(rson[pos],mid+1,r,ll,rr);
 41     }
 42 }tree;
 43 
 44 namespace SAM {
 45     int ch[maxn][26],fa[maxn],len[maxn],deg[maxn],last,root,cnt;
 46     int rit[maxn],pos[maxn],roots[maxn],bst[maxn],f[maxn];
 47     int seq[maxn],qlen;
 48     
 49     inline int NewNode(int li) {
 50         len[++cnt] = li;
 51         return cnt;
 52     }
 53     inline void extend(int x,int at) {
 54         int p = last;
 55         int np = NewNode(len[p]+1); rit[np] = pos[np] = at;
 56         while( p && !ch[p][x] ) ch[p][x] = np , p = fa[p];
 57         if( !p ) fa[np] = root;
 58         else {
 59             int q = ch[p][x];
 60             if( len[q] == len[p] + 1 ) fa[np] = q;
 61             else {
 62                 int nq = NewNode(len[p]+1);
 63                 memcpy(ch[nq],ch[q],sizeof(ch[q])) , fa[nq] = fa[q] , pos[nq] = pos[q];
 64                 fa[np] = fa[q] = nq;
 65                 while( p && ch[p][x] == q ) ch[p][x] = nq , p = fa[p];
 66             }
 67         }
 68         last = np;
 69     }
 70     inline void build() {
 71         last = root = NewNode(0);
 72         for(int i=1;i<=li;i++) extend(in[i]-'a',i);
 73     }
 74     inline void topo() {
 75         for(int i=1;i<=cnt;i++) if( fa[i] ) ++deg[fa[i]];
 76         queue<int> q;
 77         for(int i=1;i<=cnt;i++) if( !deg[i] ) q.push(i);
 78         while( q.size() ) {
 79             const int pos = q.front(); q.pop() , seq[++qlen] = pos;
 80             if( pos == root ) continue;
 81             if( rit[pos] ) {
 82                 int t = 0;
 83                 tree.insert(t,1,li,rit[pos]);
 84                 roots[pos] = tree.merge(roots[pos],t,1,li);
 85             }
 86             roots[fa[pos]] = tree.merge(roots[fa[pos]],roots[pos],1,li);
 87             if( !--deg[fa[pos]] ) q.push(fa[pos]);
 88         }
 89         reverse(seq+1,seq+1+qlen);
 90     }
 91     inline void getans() {
 92         f[root] = 1 , bst[root] = root;
 93         for(int i=2;i<=qlen;i++) {
 94             const int now = seq[i] , milen = len[fa[now]] + 1;
 95             if( fa[now] == root ) {
 96                 f[now] = 1 , bst[now] = now;
 97             } else {
 98                 bst[now] = bst[fa[now]] , f[now] = f[bst[now]];
 99                 const int ql = pos[now] - len[now] + len[bst[now]];
100                 const int qr = pos[now] - milen + len[bst[now]];
101                 if( tree.query(roots[bst[now]],1,li,ql,qr) ) f[now]++ , bst[now] = now;
102             }
103             ans = max( ans , f[now] );
104         }
105     }
106 }
107 
108 int main() {
109     scanf("%s",in+1) , li = strlen(in+1);
110     SAM::build() , SAM::topo();
111     SAM::getans();
112     printf("%d
",ans);
113     return 0;
114 }
    View Code


    T2:


    显然不管是不是DAG，直接跑最小割都是WA的，不服见下图。
    另外显然环上的边是一定不能割的，否则绕环一圈再走的路径上会有两条被割掉的边，我们可以先tarjan大力缩环变成DAG。
    考虑如何防止一条路径上的边被割多次，我们能让这条路径上所有靠后的点向靠前的点连边容量inf，如果割掉后面的边且割掉前面的边相当于没割......
    这建图点数O(n)，边数O(m^2)。
    考虑怎么优化，由于inf具有传递性，所以我们让每个靠后的点单独向前面的点连边就行了，也就是，对于每一条边连接容量inf的反向边。
    对于环的话，由于inf边的存在，我们显然不会割环上的边，于是连tarjan也省了。
    然而这样是不行的，对于不在1~n路径上的边，不能连inf边，否则跑出的答案会比正确答案大(反例见上图)。
    关于无解，直接判断最小割是否为inf就好了。
    代码:

      1 #include<iostream>
  2 #include<cstdio>
  3 #include<cstring>
  4 #include<algorithm>
  5 #include<queue>
  6 typedef long long int lli;
  7 using namespace std;
  8 const int maxn=1e3+1e2,maxe=2e3+1e2;
  9 const lli inf=0x3f3f3f3f3f3f3f3fll;
 10 
 11 namespace Flow {
 12     int s[maxn<<1],t[maxe<<2],nxt[maxe<<2],cnt=1;
 13     lli f[maxe<<2];
 14     int dep[maxn],st,ed;
 15     
 16     inline void coredge(int from,int to,lli flow) {
 17         t[++cnt] = to , f[cnt] = flow ,
 18         nxt[cnt] = s[from] , s[from] = cnt;
 19     }
 20     inline void singledge(int from,int to,lli flow) {
 21         coredge(from,to,flow) , coredge(to,from,0);
 22     }
 23     inline bool bfs() {
 24         memset(dep,-1,sizeof(dep)) , dep[st] = 0;
 25         queue<int> q; q.push(st);
 26         while( q.size() ) {
 27             const int pos = q.front(); q.pop();
 28             for(int at=s[pos];at;at=nxt[at])
 29                 if( f[at] && !~dep[t[at]] )
 30                     dep[t[at]] = dep[pos] + 1 , q.push(t[at]);
 31         }
 32         return ~dep[ed];
 33     }
 34     inline lli dfs(int pos,lli flow) {
 35         if( pos == ed ) return flow;
 36         lli ret = 0 , now = 0;
 37         for(int at=s[pos];at;at=nxt[at])
 38             if( f[at] && dep[t[at]] > dep[pos] ) {
 39                 now = dfs(t[at],min(flow,f[at]));
 40                 ret += now , flow -= now ,
 41                 f[at] -= now , f[at^1] += now;
 42                 if( !flow ) return ret;
 43             }
 44         if( !ret ) dep[pos] = -1;
 45         return ret;
 46     }
 47     inline lli dinic() {
 48         lli ret = 0 , now = 0;
 49         while( bfs() ) {
 50             while( now = dfs(st,inf) ) {
 51                 if( now == inf ) return -1; //No solution .
 52                 ret += now;
 53             }
 54         }
 55         return ret;
 56     }
 57     inline void reset(int n) {
 58         memset(s,0,sizeof(s))  ,cnt = 1;
 59         st = 1 , ed = n;
 60     }
 61 }
 62 
 63 struct Graph {
 64     int s[maxn],t[maxe<<1],nxt[maxe<<1],vis[maxn],cnt;
 65     
 66     inline void addedge(int from,int to) {
 67         t[++cnt] = to , nxt[cnt] = s[from] , s[from] = cnt;
 68     }
 69     inline void dfs(int pos) {
 70         if( vis[pos] ) return;
 71         vis[pos] = 1;
 72         for(int at=s[pos];at;at=nxt[at]) dfs(t[at]);
 73     }
 74     inline void reset() {
 75         memset(s,0,sizeof(s)) , memset(vis,0,sizeof(vis)) , cnt = 0;
 76     }
 77 }gra,inv;
 78 
 79 int x[maxe],y[maxe],f[maxe];
 80 
 81 inline void build(int m) {
 82     for(int i=1;i<=m;i++) {
 83         Flow::singledge(x[i],y[i],f[i]);
 84         if( gra.vis[x[i]] && inv.vis[y[i]] ) Flow::singledge(y[i],x[i],inf);
 85     }
 86 }
 87 
 88 inline void reset(int n) {
 89     Flow::reset(n);
 90     gra.reset() , inv.reset();
 91 }
 92 
 93 int main() {
 94     static int T,n,m;
 95     scanf("%d",&T);
 96     while(T--) {
 97         scanf("%d%d",&n,&m) , reset(n);
 98         for(int i=1;i<=m;i++) {
 99             scanf("%d%d%d",x+i,y+i,f+i);
100             gra.addedge(x[i],y[i]) , inv.addedge(y[i],x[i]);
101         }
102         gra.dfs(1) , inv.dfs(n);
103         build(m);
104         printf("%lld
",Flow::dinic());
105     }
106     return 0;
107 }
    View Code


    T3:


    直接放官方题解吧......


    代码:

     1 #include<iostream>
 2 #include<cstdio>
 3 #include<cstring>
 4 #include<algorithm>
 5 #define debug cout
 6 using namespace std;
 7 const int maxn=1e6+1e2;
 8 
 9 int s[maxn],t[maxn<<1],nxt[maxn<<1],fa[maxn],w[maxn],sons[maxn];
10 int n,a,b;
11 
12 inline  void coredge(int from,int to) {
13     static int cnt = 0;
14     t[++cnt] = to , nxt[cnt] = s[from] , s[from] = cnt;
15 }
16 inline void doubledge(int a,int b) {
17     coredge(a,b) , coredge(b,a);
18 }
19 inline void update(int &mx,int &sec,const int &now) {
20     if( now >= mx ) sec = mx , mx = now;
21     else if( now > sec ) sec = now;
22 }
23 inline void dfs(int pos) {
24     int mx = 0 , sec = 0;
25     for(int at=s[pos];at;at=nxt[at])
26         if( t[at] != fa[pos] ) {
27             fa[t[at]] = pos , ++sons[pos];
28             dfs(t[at]) , update(mx,sec,w[t[at]]);
29         }
30     w[pos] = sec + sons[pos];
31 }
32 inline bool check(int lim) {
33     int fs = 0 , tim = 0 , ret = 0 , now = a , last = -1;
34     for(int i=a;i!=b;i=fa[i]) fs += sons[i] - ( i != a );
35     while( now != b ) {
36         ++tim;
37         int sum = 0;
38         for(int at=s[now];at;at=nxt[at])
39             if( t[at] != fa[now] && t[at] != last) {
40                 if( w[t[at]] + ret + fs > lim ) ++sum , --tim;
41                 if( tim < 0 ) return 0; // No enough time .
42             }
43         ret += sum , fs -= sons[now] - ( now != a );
44         last = now , now = fa[now];
45         if( ret > lim ) return 0;
46     }
47     return ret <= lim;
48 }
49 inline int bin() {
50     int ll = -1 , rr = n << 1 , mid;
51     while( rr > ll + 1 ) {
52         mid = ( ll + rr ) >> 1;
53         if( check(mid) ) rr = mid;
54         else ll = mid;
55     }
56     return rr;
57 }
58 
59 int main() {
60     scanf("%d%d%d",&n,&b,&a);
61     for(int i=1,a,b;i<n;i++) {
62         scanf("%d%d",&a,&b) , doubledge(a,b);
63     }
64     dfs(b);
65     printf("%d
",bin());
66     return 0;
67 }
    View Code


    再有十几天就省选了，我这么弱，九成是要退役了吧。
    大概无论如何也不会坚持了吧。“你学下去”，想像BE里的红一样用生命挽救别人，然而还有谁值得我这样做呢？
    直到现在才发现，看起来很正常的我，其实是黑的......
  • 相关阅读:
    强大的异或运算-深度好文
    40-3Sum Closest
    39-Remove Duplicates from Sorted Array
    谈谈AI
    38- Majority Element
    37-Invert Binary Tree
    36-Same Tree
    35-Remove Element
    34. Swap Nodes in Pairs
    33. Implement strStr()
  • 原文地址：https://www.cnblogs.com/Cmd2001/p/8659872.html
Copyright © 2011-2022 走看看