再来一篇深度优先遍历/搜索总结?
简介:深度优先搜索算法(Depth-First-Search, DFS),最初是一种用于遍历或搜索树和图的算法,在LeetCode中很常见,虽然感觉不难,但是理解起来还是有点难度的。
简要概括,深度优先的主要思想就是“不撞南墙不回头”,“一条路走到黑”,如果遇到“墙”或者“无路可走”时再去走下一条路。
思路
假如对树进行遍历,沿着树的深度遍历树的节点,尽可能深的搜索树的分支,当达到边际时回溯上一个节点再进行搜索。如下图的一个二叉树。
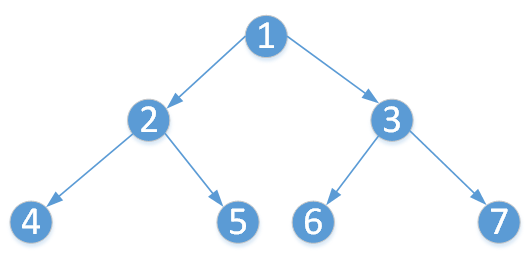
首先给出这个二叉树的深度优先遍历的结果(假定先走左子树):1->2->4->5->3->6->7
那是怎样得到这样的结果呢?
根据深度优先遍历的概念:沿着这树的某一分支向下遍历到不能再深入为止,之后进行回溯再选定新的分支。
定义节点
class TreeNode{
int val;
TreeNode left;
TreeNode right;
}
递归的方式
分别对左右子树进行递归,一直到底才进行回溯。如果不了解递归可以参考我的博客你真的懂递归吗?。
class Solution{
public void depthOrderTraversalWithRecusive(TreeNode root){
if(root == null){
return;
}
System.out.print(root.val +"->");
depthOrderTraversalWithRecusive(root.left);
depthOrderTraversalWithRecusive(root.right);
}
}
迭代的方式
上面实现了递归方式的深度优先遍历,也可以利用栈把递归转换为迭代的方式。
但是为了保证出栈的顺序,需要先压入右节点,再压左节点。
class Solution{
public void depthOrderTraversalWithoutRecusive(TreeNode root){
if(root == null) return;
Stack<TreeNode> stack = new Stack<>();
stack.push(root);
while(!stack.isEmpty()){
TreeNode node = stack.pop();
System.out.print(node.val + "->");
if(node.right != null){
stack.push(node.right);
}
if(node.left != null){
stack.push(node.left);
}
}
}
}
接着再列举个利用深度优先遍历的方式的题目
扫雷
给定一个表示游戏板的二维字符矩阵,'M'表示一个未挖出的地雷,'E'表示一个未挖出的空方块,'B' 代表没有相邻(上,下,左,右,和所有4个对角线)地雷的已挖出的空白方块,数字('1' 到 '8')表示有多少地雷与这块已挖出的方块相邻,'X' 则表示一个已挖出的地雷。
根据以下规则,返回相应位置被点击后对应的面板:
- 如果一个地雷(
'M')被挖出,游戏就结束了- 把它改为'X'。 - 如果一个没有相邻地雷的空方块(
'E')被挖出,修改它为('B'),并且所有和其相邻的方块都应该被递归地揭露。 - 如果一个至少与一个地雷相邻的空方块(
'E')被挖出,修改它为数字('1'到'8'),表示相邻地雷的数量。 - 如果在此次点击中,若无更多方块可被揭露,则返回面板。
示例
输入:
[['E', 'E', 'E', 'E', 'E'],
['E', 'E', 'M', 'E', 'E'],
['E', 'E', 'E', 'E', 'E'],
['E', 'E', 'E', 'E', 'E']]
Click : [3,0]
输出:
[['B', '1', 'E', '1', 'B'],
['B', '1', 'M', '1', 'B'],
['B', '1', '1', '1', 'B'],
['B', 'B', 'B', 'B', 'B']]
思路:根据给定的规则,当给定一个Click坐标,当不为雷的时候以此坐标为基点向四周8个方向进行深度遍历,把空格E填充为B,并且把与地雷M相连的空方块标记相邻地雷的数量。
注意 :
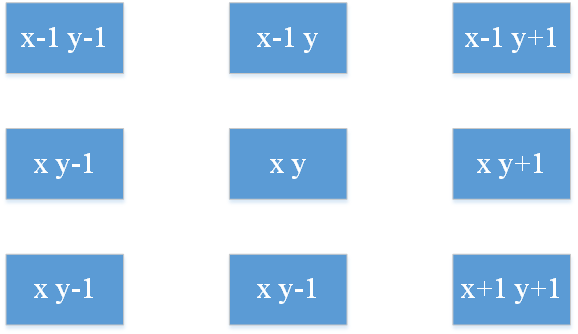
在这个题中可以沿着8个方向递归遍历,所有要注意程序中,采用了两个for循环可以实现向8个方向递归。
for(int i=-1;i<=1;i++){
for(int j=-1;j<=1;j++){
}
}
本程序需要进行返回board,在最后需要进行返回。
编程步骤
- 当
Click给出的坐标找出的是地雷,直接返回。 - 否则,进行递归,并标出雷的数量。
class Solution{
public char[][] updateBoard(char[][] board,int[] click){
if(board[click[0]][click[1]] == 'M'){
board[click[0]][click[1]] = 'X';
return board;
}
return click(board,click[0],click[1]);
}
private char[][] click(char[][] board,int x,int y){
int num = getNum(board, x,y);
if(num == 0){
board[x][y] = 'B';
}else{
board[x][y] = Character.forDigit(num,10);
return board;
}
//递归
for(int i=-1;i<=1;i++){
for(int j=-1;j<=1;j++){
if(x + i >= 0 && x + i < board.length&&y + j >=0&&y+j<board[0].length&&board[x+i][y+j]=='E'){
board = click(board,x+i,y+j);
}
}
}
return board;
}
private int getNum(char[][] board,int x,int y){
int num = 0;
for(int i=-1;i<=1;i++){
for(int j=-1;j<=1;j++){
if(x + i >= 0&&y + j >=0&&x+i<board.length&&y+j<board[0].length&&board[x+i][y+j]=='M'){
num ++;
}
}
}
return num;
}
}
总结 :深度优先遍历不仅存在树和图的数据结构中,还有很多也可以用到它。需要确定的是每一步该怎么走,有几个方向可以走。