#include <stdio.h>
#include<stdlib.h>
int main()
{
float a[3] = { 1143139122437582505939828736.0, 76482007234779498639230238720.0, 9.222452464e-39 };
printf("%d
", sizeof(float));
printf("%s
", a);
system("pause");
return 0;
}
这种表示方法通常被用于掩盖原始数据用的(比如:加密处理等)。
要想打印出Hello world,需要定义一个字符串,比如:
char str[12] = "Hello world";
字符串str一共12个字符(包含结束符),分别是:
H、e、l、l、o、空格、w、o、r、l、d、'�'
这些字符,在内存中是按照ASCII码保存的,对应的ASCII码分别是:
72,101,108,108,111,32,119,114,108,100,0
ASCII码对应的16进制数值,分别是:
0x48,0x65,0x6C,0x6C,0x6F,0x20,0x77,0x6F,0x72,0x6C,0x64,0x00
由上可知,如果想打印出helloworld,就必须在内存中有一段连续的内存,
这个内存,长度为12字节,内容(16进制)是48,65,6C....64,00。
在回过头来看看浮点数数组float a[3]。
sizeof(float)的大小是4个字节,
那么a[3]就是12个字节(即内存中有一个连续的内存,长度12字节)。
这12个字节中,有3个数字,每个数字长度4字节。
其中第一个数字1143139122437582505939828736.0,
它在内存中的16进制数据是:48 65 6C 6C(原理请百度“浮点数的二进制表示”)
同理,另外两个数字,在内存中的数据(16进制)是:
6F,20,77,6F和72,6C,64,00
这三个数字的内存数据连起来,刚好和helloword的内存数据相符。
注意,我们对字符串内存进行分析的时候,是逐个字节进行解释的
(即每个字节是什么字符)。
而我们对float[3]进行分析的时候,是每4个字节进行分析的,
(即每个float是什么数字)
同一段内存,使用不懂的视角(字符串or浮点数数组)来看,
得到的结果就是不一样的。这就是计算机的有趣之处。
扩展,如果把浮点数数组的定义,更换成下面的形式(int数组或short数组),一样可以得到hello world的。
int a[3] = {1819043144,1870078063,6581362};
short a[6] = {25928,27756,8303,28535,27762,100};
//摘自https://wenda.so.com/q/1462786652721707
浮点数是我们在程序里常用的数据类型,它在内存中到底是怎么样的形式存在,是我了解之前是觉得好神奇,以此记录,作为学习笔记。
现代计算机中,一般都以IEEE 754标准存储浮点数,这个标准的在内存中存储的形式为:
![]()
对于不同长度的浮点数,阶码与小数位分配的数量不一样,如下:

对于32位的单精度浮点数,数符分配是1位,阶码分配了8位,尾数分配了是23位。
根据这个标准,我们来尝试把一个十进制的浮点数转换为IEEE754标准表示。
例如:178.125
先把浮点数分别把整数部分和小数部分转换成2进制
整数部分用除2取余的方法,求得:10110010
小数部分用乘2取整的方法,求得:001
合起来即是:10110010.001
转换成二进制的浮点数,即把小数点移动到整数位只有1,即为:1.0110010001 * 2^111,111是二进制,由于左移了7位,所以是111
把浮点数转换二进制后,这里基本已经可以得出对应3部分的值了
数符:由于浮点数是正数,故为0.(负数为1)
阶码 : 阶码是需要作移码运算,在转换出来的二进制数里,阶数是111(十进制为7),对于单精度的浮点数,偏移值为01111111(127)[偏移量的计算是:2^(e-1)-1, e为阶码的位数,即为8,因此偏移值是127],即:111+01111111 = 10000110
尾数:小数点后面的数,即0110010001
最终根据位置填到对位的位置上:
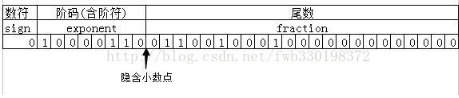
可能有个疑问:小数点前面的1去哪里了?由于尾数部分是规格化表示的,最高位总是“1”,所以这是直接隐藏掉,同时也节省了1个位出来存储小数,提高精度
---------------------
作者:Kelvin7_Feng
来源:CSDN
原文:https://blog.csdn.net/fwb330198372/article/details/70238982
版权声明:本文为博主原创文章,转载请附上博文链接!