题目描述
Secsa最近对最小生成树问题特别感兴趣。他已经知道如果要去求出一个 nn 个点、 mm 条边的无向图的最小生成树有一个Krustal算法和另一个Prim的算法。另外,他还知道,某一个图可能有多种不同的最小生成树。例如,下面图3中所示的都是图2中的无向图的最小生成树:
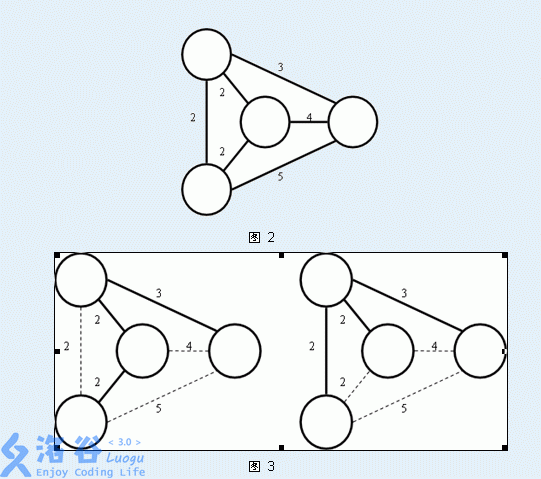
当然啦,这些都不是今天需要你解决的问题。Secsa想知道对于某一条无向图中的边AB,至少需要多少代价可以保证AB边在这个无向图的最小生成树中。为了使得AB边一定在最小生成树中,你可以对这个无向图进行操作,一次单独的操作是指:先选择一条图中的边 P1P2,再把图中除了这条边以外的边,每一条的权值都减少 11 。如图4所示就是一次这样的操作:

题解
-
我们可以发现让其余所有边都减1和让自己加1没什么区别
-
考虑kruskal的过程,首先边权大于这条边的是不用考虑的
-
考虑把那些边权比这条边小的调节到比这条边大,这样就相当于在生成树上去掉了这条边
-
至于调大到多少自然是使得边权恰好大1
-
让这条边必然存在就一定得让这条边链接的两个点不连通,于是我们把在生成树上去掉这条边看成割断这条边,于是这就是一个最小割
代码
1 #include <queue> 2 #include <cstdio> 3 #include <iostream> 4 #include <algorithm> 5 using namespace std; 6 const int N=1010; 7 queue<int> Q; 8 struct edge{int to,from,w;}e[N*4]; 9 struct node{int u,v,w,o;}E[N]; 10 int n,m,S,T,k,t,cnt=1,ans,head[N],d[N],cur[N]; 11 int cmp(node a,node b) { return a.w==b.w?a.o<b.o:a.w<b.w; } 12 void insert(int x,int y,int w) 13 { 14 e[++cnt].to=y,e[cnt].from=head[x],head[x]=cnt,e[cnt].w=w; 15 e[++cnt].to=x,e[cnt].from=head[y],head[y]=cnt,e[cnt].w=0; 16 } 17 int bfs() 18 { 19 for(int i=1;i<=n;i++) d[i]=0,cur[i]=head[i]; 20 Q.push(S),d[S]=1; 21 while (!Q.empty()) 22 { 23 int u=Q.front(); Q.pop(); 24 for (int i=head[u];i;i=e[i].from) if (!d[e[i].to]&&e[i].w) d[e[i].to]=d[u]+1,Q.push(e[i].to); 25 } 26 return d[T]; 27 } 28 int dfs(int x,int now) 29 { 30 if (x==T||!now) return now; 31 int flow=0,ff; 32 for (int& i=cur[x];i;i=e[i].from) 33 if (d[e[i].to]==d[x]+1) 34 { 35 ff=dfs(e[i].to,min(now,e[i].w)); 36 if (ff<=0) continue; 37 now-=ff,flow+=ff,e[i].w-=ff,e[i^1].w+=ff; 38 if (!now) break; 39 } 40 return flow; 41 } 42 int main() 43 { 44 scanf("%d%d%d",&n,&m,&k); 45 for (int i=1;i<=m;i++) scanf("%d%d%d",&E[i].u,&E[i].v,&E[i].w); 46 E[k].o=1,S=E[k].u,T=E[k].v,t=E[k].w,sort(E+1,E+m+1,cmp); 47 for (int i=1;i<=m;i++) { if (E[i].o) break; insert(E[i].u,E[i].v,t-E[i].w+1),insert(E[i].v,E[i].u,t-E[i].w+1); } 48 while (bfs()) ans+=dfs(S,999999999); printf("%d",ans); 49 }