[欧拉函数][卷积] Luogu P3768 简单的数学

题目描述

由于出题人懒得写背景了，题目还是简单一点好。

输入一个整数n和一个整数p，你需要求出(∑i=1n∑j=1nijgcd(i,j)) mod p(sum_{i=1}^nsum_{j=1}^n ijgcd(i,j))~mod~p(∑i=1n​∑j=1n​ijgcd(i,j)) mod p，其中gcd(a,b)表示a与b的最大公约数。

题解

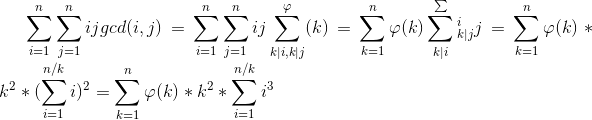
代码

#include <map>
#include <cstdio>
#include <iostream>
#define N 4600000
#define sqr(x) (x)*(x)
#define ll long long
using namespace std;
ll p,n,inv,pos,r,phi[N],q[N],bz[N],s[N];
map<ll,ll> m;
ll calc1(ll x) { x%=p; return x*(x+1)%p*(2*x+1)%p*inv%p; }
ll calc2(ll x) { x%=p; return sqr((x*(x+1)/2)%p)%p; }
ll ksm(ll a,ll b) { ll r=1; for (;b;b>>=1,a=a*a%p) if (b&1) r=r*a%p; return r; }
ll calc(ll x)
{
    if (x<N) return s[x];
    if (m[x]) return m[x];
    ll pos,r=calc2(x);
    for (ll i=2;i<=x;i=pos+1) pos=x/(x/i),r=(r-(calc1(pos)-calc1(i-1)+p)%p*calc(x/i)%p)%p;
    m[x]=r=(r+p)%p; return r;
}
int main()
{
    scanf("%lld%lld",&p,&n),inv=ksm(6,p-2),phi[1]=1;
    for (ll i=2;i<N;i++)
    {
        if (!bz[i]) q[++q[0]]=i,phi[i]=i-1;
        for (ll j=1;j<=q[0];j++)
            if (i*q[j]<N)
            {
                bz[i*q[j]]=1;
                if (i%q[j]==0) { phi[i*q[j]]=phi[i]*q[j]; break; }
                phi[i*q[j]]=phi[i]*(q[j]-1);
            }
            else break;
    }
    for (ll i=1;i<N;i++) s[i]=(s[i-1]+i*i%p*phi[i]%p)%p;
    for (ll i=1;i<=n;i=pos+1) pos=n/(n/i),r=(r+(calc(pos)-calc(i-1)+p)%p*calc2(n/i)%p)%p;
    printf("%lld",r=(r+p)%p); 
}