题解
- 50%的做法其实很简单,
- 设f[i][0/1]现在在枚举到i,状态为0或1(上升或下降),枚举一个起始点,O(N)跑一次
- 最后的时间复杂度就是O(N(N2))
- 100%做法:
- 设f[i][0..1][0..1]表示在第i个点,状态为0或1(上升或下降),是否改变过状态(0或1)。
- 状态转移方程就是
-
//不用改变状态:
f[i][j][0]=f[i-1][j][0]+abs(a[i]-a[i-1]);
f[i][j][1]=min(f[i-1][j][1],min(f[i-1][j^1][0],f[i-1][j^1][1])+m)+abs(a[i]-a[i-1]);
//要改变状态:
f[i][j][0]=f[i-1][j][0]+sqr(a[i]-a[i-1]);
f[i][j][1]=min(f[i-1][j][1],min(f[i-1][j^1][0],f[i-1][j^1][1])+m)+sqr(a[i]-a[i-1]);
- 那么我们考虑一下对于改变状态的奇偶性(下面的图都是将环拆成一条链)
- ①如果没有改变过状态,很容易统计答案 ans=min(f[n][0][0],f[n][1][0])
- ②如果改变过奇数次状态(上图!!)
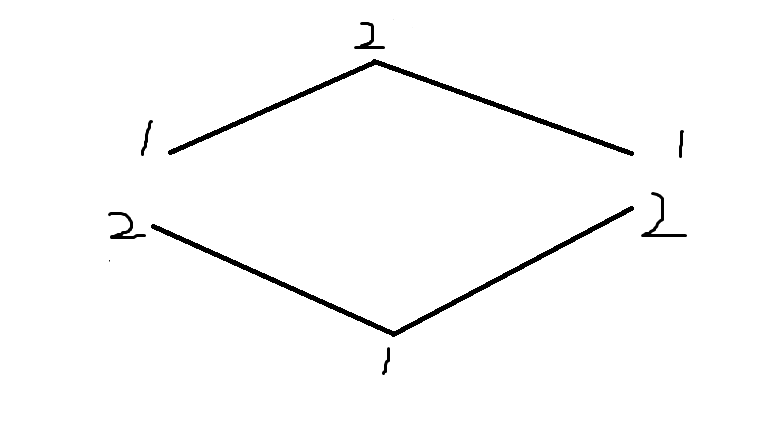
- 显然,顺时针和逆时针改变的次数都一样,所以ans=min(f[n][0][1],f[n][1][1])
- ③如果改变过偶数次状态
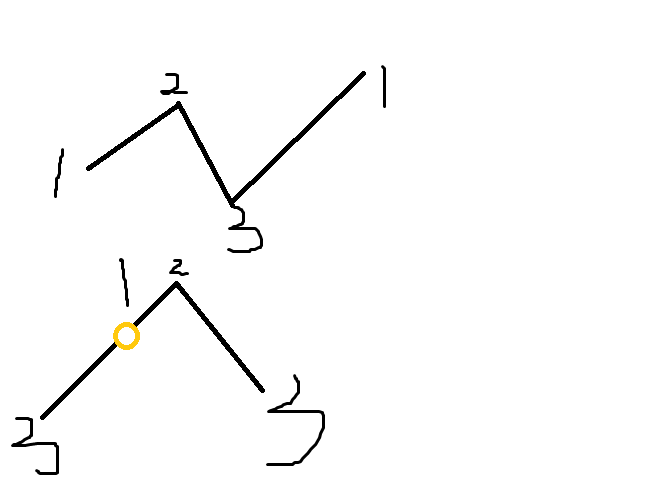
- 显然这样的话,顺时针和逆时针的改变的状态的次数是不一样的
- 所以要减去一个m
- ans=min(f[n][0][0]-m,f[n][1][0]-m)
代码
1 #include<iostream>
2 #include<cstdio>
3 #include<cstdlib>
4 #include<memory.h>
5 using namespace std;
6 int a[10010],n,m;
7 long long f[10010][2][2];
8 long long sqr(long long x){return x*x;}
9 void dp()
10 {
11 f[0][0][1]=f[0][1][1]=0x7fffffff;
12 for(int i=1;i<=n;i++)
13 for(int j=0;j<2;j++)
14 if ((a[i]<a[i-1])^j)
15 {
16 f[i][j][0]=f[i-1][j][0]+abs(a[i]-a[i-1]);
17 f[i][j][1]=min(f[i-1][j][1],min(f[i-1][j^1][0],f[i-1][j^1][1])+m)+abs(a[i]-a[i-1]);
18 }
19 else
20 {
21 f[i][j][0]=f[i-1][j][0]+sqr(a[i]-a[i-1]);
22 f[i][j][1]=min(f[i-1][j][1],min(f[i-1][j^1][0],f[i-1][j^1][1])+m)+sqr(a[i]-a[i-1]);
23 }
24 }
25 int main()
26 {
27 scanf("%d%d",&n,&m);
28 for(int i=0;i<n;i++) scanf("%d",&a[i]);
29 a[n]=a[0];
30 memset(f,0,sizeof(f));
31 dp();
32 long long ans=min(min(f[n][0][0],f[n][0][1]),min(f[n][1][0],f[n][1][1]));
33 memset(f,0,sizeof(f)); f[0][0][0]=0x7fffffff;
34 dp();
35 ans=min(ans,f[n][1][1]-m);
36 memset(f,0,sizeof(f)); f[0][1][0]=0x7fffffff;
37 dp();
38 ans=min(ans,f[n][0][1]-m);
39 cout<<ans;
40 return 0;
41 }

