#define MAXSIZE 10 typedef struct { int r[MAXSIZE + 1]; int length; }SqList; void swap(SqList *L,int i, int j) { int temp = L->r[i]; L->r[i] = L->r[j]; L->r[j] = temp; }
冒泡排序:基本思想是两两比较相邻记录的关键字,如果反序则交换,直到没有反序的为止。

1 void BubbleSort(SqList *L) 2 { 3 // int i, j; 4 bool flag = TRUE; 5 for (int i = 1; i < L->length && flag; ++i) 6 { 7 flag = FALSE; 8 for(int j = L->length-1;j >= i; j--) 9 { 10 if(L->r[j] > L->r[j+1]) 11 swap(L,j,j+!); 12 flag = TRUE; 13 } 14 } 15 }
//设置flag标志位是为解决类似{2,1,3,4,5,6,7,8}这样只需
//交换1和2,之后的数据不需比较的情况,可以有效节省开销
//复杂度分析:1、最好的情况:原序列本身已排好序有改进算法可知
//只需n-1次的比较,没有数据交换,时间复杂度为O(n)
//2、最坏情况:即待排序序列为完全逆序,此时需要比较n(n-1)/2次
//并作等数量级的移动,总的时间复杂度为O(n*n)
//冒泡排序的思想即不断地进行交换,通过交换完成最终的排序

1 template<class T> 2 void BubbleSort(T a[], int n) 3 { 4 int i, j, k; 5 T t; 6 7 for (i = n-1; i > 0; i = k) //将i设置为被交换的最后一对元素中较小的下标 8 { 9 for(j = k = 0; j < i; j++) 10 { 11 if(a[j] < a[j+1]) 12 { 13 t = a[j]; 14 a[j] = a[j+1]; 15 a[j+1] = t; 16 17 k = j; //如有交换发生,记录较小元素的下标 18 } 19 } 20 } 21 }
插入排序:
void InsertSort(SqList *L) { int i, j; for(i=2;i<=L->length;i++) { if(L->r[i]<L->r[i-1]) { L->r[0] = L->r[i]; for(j=i-1;L->r[j]>L->r[0];j--) { L->r[j+1] = L->r[j]; } L->r[j+1] = L->r[0]; } } }
//j = i-1只在首次进入for循环时才使用
//L->r[0] use to be sentry
//以第二次循环为例说明排序过程:
//i=3;判断r[3]<r[2]成立进入if语句;先将r[3]赋给sentry r[0],保存下来
//然后进入for循环:for(j=2;r[2]>r[0];j--),当j=2时,满足r[2]>r[0](==r[3])的条件,
//故将r[2]赋值给r[3],j减1变为1,然后判断r[1]是否大于r[0],若是,则满足for循环条件,
//进入for循环内部,将r[1]赋值给r[2],j减1变为0,之后不再满足for循环条件跳出for循环语句
//最后再将起初放入r[0]的r[3]赋值给r[1],这样就完成了r[1],r[2],r[3]三者的比较和排序;
//算法复杂度的分析:
//从空间来看只需要一个记录的辅助空间,故而主要是看他的时间复杂度
//最好的情况:原始序列顺序排列,只是进行比较,共n-1次,时间复杂度为O(n),因为内层
//for循环的检测总是立即判定不成立而终止,所以分析可知如果对于输入几乎是顺序排列的
//的序列,则插入排序竟会运行的很快
//最坏的情况:原始序列逆序排列,O(n*n)
//关键分析排序的平均情形:
下面附上C++实现代码:

1 #include <iostream> 2 using namespace std; 3 4 template <class T> 5 void InsertionSort(T A[], int n) 6 { 7 int i, j; 8 T temp; 9 10 for(i=1; i<n;i++) 11 { 12 temp = A[i]; 13 j = i; 14 while(j>0 && A[j-1]>temp) 15 { 16 A[j] = A[j-1]; 17 j--; 18 } 19 A[j] = temp; 20 21 for(int k=0; k<n; k++) 22 { 23 cout << A[k] << " "; 24 25 } 26 cout << endl; 27 } 28 } 29 30 int main() 31 { 32 int i; 33 int data[] = {1,3,5,7,9,13,15,17,2,4,6,8,14,16}; 34 35 cout << "Before sort:" << endl; 36 for(i=0;i<14;i++) 37 { 38 cout << data[i] << " "; 39 } 40 cout << endl; 41 42 cout << "Sorting..." << endl; 43 InsertionSort(data, 14); 44 45 cout << "After sort..." << endl; 46 for(i=0;i<14;i++) 47 { 48 cout << data[i] << " "; 49 } 50 cout << endl; 51 52 }
核心算法即line 10 --- line 19
运行结果:

//Shell Sort:Improvement in Select Sort
//希尔排序对于输入数据相当不敏感,即处理逆序或随机顺序的序列不会遭受显著的速度降级
//也不会像选择排序和冒泡排序对于已排好序的序列的那样引人注目的速度
//唯一的负面特性是:不是一种稳定的排序
//希尔排序基于插入排序的两点性质而提出的改进方法:
//1、插入排序在对几乎已经排好序的数据操作时,效率高,即可以达到线性排序的效率
//2、但插入排序一般来说是低效的, 因为插入排序每次只能将数据移动一位

1 void SellSort(Sqlist *L) 2 { 3 int i, j; 4 int increment = L->length; 5 do 6 { 7 increment = increment/3+1;//保证最后一次循环增量为1,即采用选择排序 8 for(i = increment+1;i<=L->length;i++) 9 { 10 if(L->r[i]<L->r[i-increment]) 11 { 12 L->r[0] = L-<r[i]; 13 for(j=i-increment;j>0&&L->r[0]<L->r[j];j-=increment) 14 L->r[j+increment] = L->r[j]; 15 L->r[j+increment] = L->r[0]; 16 } 17 } 18 } 19 while(increment>1); 20 }
//关键是增量的选取
//伪代码

1 input: an array a of length n with array elements numbered 0 to n − 1 2 inc ← round(n/2) 3 while inc > 0 do: 4 for i = inc .. n − 1 do: 5 temp ← a[i] 6 j ← i 7 while j ≥ inc and a[j − inc] > temp do: 8 a[j] ← a[j − inc] 9 j ← j − inc 10 a[j] ← temp 11 inc ← round(inc / 2.2)
//Note:上面C代码的实现与伪码的不同存在于两点:
//1、增量的选取不同,这个并没有权威的标准,不同的增量选择会影响实际的运算复杂度
//2、程序实现中采用数组的第0个元素作为额外的存储空间,而伪码中采用新建的变量temp
//其实比较选择排序和希尔排序可以看出代码实现很相似,只是增量的问题。。
希尔排序算法实现过程描述:(附代码)

1 template <class> 2 void ShellSort(T a[], int n) 3 { 4 int i, j, k; 5 T t; 6 7 k = n/2; //起始增量 8 while(k > 0) //循环至增量为1时结束 9 { 10 for(i = k; i < n; i++) 11 { 12 t = a[i]; 13 for(j = j - k; j >= 0; j -= k) 14 { 15 a[j+k] = a[j]; 16 } 17 18 a[j+k] = t; 19 } 20 21 k /= 2; //缩小增量 22 } 23 }
从上述算法实现中可以明显看出希尔排序是对插入排序的升级版,line 13--line 16的内部for循环实质就是插入排序的改动版
其核心思想即为插入法+缩小增量,
首先要明确一下增量的取法:
第一次增量的取法为: d=count/2;
第二次增量的取法为: d=(count/2)/2;
最后一直到: d=1;
看上图观测的现象为:
d=3时:将40跟50比,因50大,不交换。
将20跟30比,因30大,不交换。
将80跟60比,因60小,交换。
d=2时:将40跟60比,不交换,拿60跟30比交换,此时交换后的30又比前面的40小,又要将40和30交换,如上图。
将20跟50比,不交换,继续将50跟80比,不交换。
d=1时:这时就是前面讲的插入排序了,不过此时的序列已经差不多有序了,所以给插入排序带来了很大的性能提高。
堆排序:
//堆排序的基本思想:以大项堆为例:
//将待排序的序列构造成一个大顶堆;此时,整个序列的最大值就是堆顶的根节点
//将它移走(其实就是将其与对数组的末尾元素交换,此时末尾元素就是最大值),
//然后将剩余的n-1个序列重新构造成一个新堆,这样就会得到n个元素中的次小值。
//如此反复进行,便能得到一个有序序列了
//至此就首先需要解决两个问题:
//1、如何有一个无序序列构建一个堆?
//2、如何在输出堆顶元素后,调整剩余元素成为一个新的堆?

1 /*对顺序表L进行堆排序*/ 2 void HeapSort(SqList *L) 3 { 4 int i; 5 for(i=L->length/2;i>0;i--) 6 { 7 HeapAdjust(L,i,L->length); 8 } 9 for(i=L->length;i>1;i--) 10 { 11 swap(L,1,i);//将堆顶记录与当前未经排序子序列的最后一个记录想交换 12 HeapAdjust(L,1,i-1);//将L[1...i-1]重新调整为大项堆 13 } 14 }



1 void HeapAdjust(SqList *L, int s, int m) 2 { 3 int temp, j; 4 temp = L->r[s]; 5 for(j=2*s;j<=m;j*=2) 6 { 7 if(j<m && L->r[j]<L->r[j+1]) 8 ++j; 9 if(temp>=L->r[j]) 10 break; 11 L->r[s] = L->r[j]; 12 s = j; 13 } 14 L->r[s] = temp; 15 }
//思路分析:以s=4为例说明:
//r[4]=30,首先将其用一变量temp存储起来,由于堆实质就是一个完全二叉树,
//所以接下来要比较该节点与其子节点值的大小,由完全二叉树性质可知,节点i
//的左右子节点标号分别为2i和2i+1,故而for循环从j=2s开始执行,递增用j*=2
//接下来首先判断j是否小于9,即是否为最后一个节点,并且同时判断左节点的值
//是否小于右节点,当同时满足时说明1、该节点不是最后一个节点,有孩子节点
//2、该节点的左孩子值小于右孩子,则用j来标记较大值的下标;接着再判断r[j]
//是否不大于其父节点的值,若是,则父节点的值即为最大,退出for循环;若否,则将
//r[j]的值赋给r[s],也即父节点,从而实现了一个节点系统的最大堆实现。
//然后将j赋给s,此处的理解参照图示以s=1的那次循环来说明:

由节点1和其子节点比较交换后可知节点3的值变为50,而此时节点3作为父节点其值又小于节点7的值
可知不满足最大堆的性质,故而还需进行最大堆调整,所以程序中在if函数体最后将j赋给s,进而进入下次for
循环继续比较。。。
堆排序算法复杂度分析:它的运行时间主要消耗在初始构建堆和在重建堆时的反复筛选上
在构建堆的过程中,因为我们是完全二叉树从最下层最右边的非终端节点开始构建,将它与
孩子进行比较和一些有必要的交换,对于每个非终端节点来说,最多进行两次比较和交换操作,
因此整个构建堆的时间复杂度为O(n)。
在正式排序时,第i次去堆顶记录重建堆需要O(logi)的时间(完全二叉树的某个节点到根节点的距离为floor(logi)+1,(注:floor为向下舍入))并且需要取n-1次堆顶记录,因此重建堆的时间复杂度为O(nlogn)
故总的来说,堆排序的时间复杂度为O(nlogn).堆排序对于原始序列(记录)的状态不敏感,
所以无论最好、最坏还是平均时间复杂度都是O(nlogn),因此从性能上要远优于冒泡,选择和直接插入的O(n*n)的时间复杂度。
从空间复杂度的角度上,它只有一个用来交换的暂存空间,也很不错。由于比较和交换都是跳跃式的进行,堆排序不是一种稳定的排序。一般适合于排序序列个数较多的情况。
下面是Keith Schwarz的代码实现:

1 /**************************************************************** 2 * File: Heapsort.hh 3 * Author: Keith Schwarz (htiek@cs.stanford.edu) 4 * 5 * Implementation of the Heapsort algorithm, a @(n lg n) sort 6 * algorithm (here, @ is the ASCII stand-in for big theta). 7 * Heapsort works by rearranging the elements of the input array 8 * into a binary max-heap, then continuously dequeueing the max 9 * element and placing it at the back of the array. It is one 10 * of the fastest and most reliable sorting algorithms, and is 11 * a key building block of various hybrid sorts such as 12 * introsort. 13 * 14 * The algorithm runs in two phases. In the first phase, in 15 * O(n) time, the algorithm rearranges the elements in the 16 * range to put them into a max-heap. In the second phase, 17 * the algorithm continuously removes the maximum element 18 * from the heap, places it at the last spot in the array, 19 * then repeats. This step takes @(n lg n) and accounts 20 * for the majority of the runtime. 21 * 22 * Note that this could be done using the STL make_heap 23 * and sort_heap algorithms. However, in the interests 24 * of explaining this algorithm in more detail, I've 25 * avoided doing so here. 26 * 27 * The key algorithm in Heapsort is the heap join algorithm. 28 * Heap join takes as input two max-heaps and a new value, 29 * then produces a single max-heap from the elements. For 30 * example, given the singleton max-heaps 1 and 5 and the 31 * new element 3, the heap join algorithm would begin by 32 * constructing the tree 33 * 34 * 3 35 * / 36 * 1 5 37 * 38 * Then balancing it to form 39 * 40 * 5 41 * / 42 * 1 3 43 * 44 * This algorithm is useful for two reasons. First, it allows 45 * for an O(n) algorithm for constructing a max-heap from a 46 * collection of data. This algorithm works by taking n/2 of 47 * the elements and creating singleton binary heaps from them. 48 * Next, half of the remaining elements (n/4 of the original 49 * elements) are used to join these singleton heaps together 50 * into n/4 max-heaps. A remaining half of the remaining 51 * elements (n/8 of the original elements) are then used to 52 * join these trees together, etc. At the end, all of the 53 * elements are joined together into a single max-heap of 54 * all the data. 55 * 56 * Second, this algorithm also provides an efficient means for 57 * rebalancing a heap after removing the max element. When the 58 * max element is removed, the heap is split into two different 59 * max heaps. An arbitrary leaf of the tree (chosen specifically 60 * so that the resulting tree is complete) is then removed from 61 * one of these two heaps, then used in the join step to 62 * rebalance the heaps. 63 * 64 * The implementation of this algorithm is simple. Given two 65 * max-heaps and a new element, if the new element is bigger than 66 * the roots of both max-heaps, then by transitivity it is bigger 67 * than all of the elements of both heaps, and so the max-heap 68 * formed by putting the new element as the root is a max-heap. 69 * Otherwise, the larger of the roots of the two trees is 70 * removed, splitting its tree in two, and that element is 71 * placed as the root of the new heap. The element used to 72 * join the trees is then used to recursively join together the 73 * two new disjoint trees. In a sense, this element is 74 * "bubbled down" through the tree until it comes to rest. 75 * 76 * The main complexity of the code is that all of these trees 77 * are represented implicitly in the elements of the range to 78 * be sorted. The range of elements is structured so that 79 * the first element is the root of a max-heap whose children 80 * are in the second and third positions. In general, the 81 * elements are sorted so that the range is a max-heap where 82 * node i has children at positions 2 * i + i and 2 * i + 2. 83 * In the first step of this algorithm, this heap is built 84 * up from right-to-left by constructing the leaves of the 85 * max-heap using the latter elements of the array. In 86 * the second stage, the max-heap is deconstructed, putting 87 * the maximum element at the end of the sequence and 88 * rebalancing the tree. 89 */ 90 #ifndef Heapsort_Included 91 #define Heapsort_Included 92 93 #include <iterator> 94 #include <functional> 95 #include <algorithm> 96 97 /** 98 * Function: Heapsort(RandomIterator begin, RandomIterator end); 99 * Usage: HeapSort(v.begin(), v.end()); 100 * ------------------------------------------------------------- 101 * Sorts the elements in the range [begin, end) into ascending 102 * order using the heapsort algorithm. 103 */ 104 template <typename RandomIterator> 105 void Heapsort(RandomIterator begin, RandomIterator end); 106 107 /** 108 * Function: Heapsort(RandomIterator begin, RandomIterator end, 109 * Comparator comp); 110 * Usage: HeapSort(v.begin(), v.end(), comp); 111 * ------------------------------------------------------------- 112 * Sorts the elements in the range [begin, end) into ascending 113 * order using the heapsort algorithm. The elements are compared 114 * using the comparator comp, which should be a strict weak 115 * ordering. 116 */ 117 template <typename RandomIterator, typename Comparator> 118 void Heapsort(RandomIterator begin, RandomIterator end, 119 Comparator comp); 120 121 /* * * * * Implementation Below This Point * * * * */ 122 namespace heapsort_detail { 123 124 /** 125 * Function: HeapJoin(RandomIterator begin, RandomIterator heapStart, 126 * RandomIterator end, Comparator comp); 127 * ----------------------------------------------------------------- 128 * Given a range of elements [begin, end) and a suffix [heapStart, end) 129 * that represents two max-heaps with the element to join them at the 130 * top, applies the heap join algorithm to rearrange the elements of 131 * [heapStart, end) such that the result is a max-heap according to 132 * comp. The reason for also passing in the argument begin defining 133 * the beginning of the heap is so that it is possible to compute 134 * the positions of the children of each node in the sequence by 135 * using the absolute position in the sequence. 136 */ 137 template <typename RandomIterator, typename Comparator> 138 void HeapJoin(RandomIterator begin, RandomIterator heapStart, 139 RandomIterator end, Comparator comp) { 140 /* Utility typedef. This type represents "the distance between two 141 * RandomIterators." 142 */ 143 typedef typename std::iterator_traits<RandomIterator>::difference_type diff_t; 144 145 /* Cache the number of elements in the range. */ 146 const diff_t kNumElems = distance(begin, end); 147 148 /* The initial position of the max element is at the top of the 149 * heap, which is at the index given by the offset of heapStart 150 * into the range starting at begin. 151 */ 152 diff_t position = distance(begin, heapStart); 153 154 /* Iterate until we have no children. The first child of node i 155 * is at position 2 * (i + 1) - 1 = 2 * i + 1, and the second 156 * at 2 * (i + 1) + 1 - 1 = 2 * i + 2. 157 */ 158 while (2 * position + 1 < kNumElems) { 159 /* Get the index of the child we will compare to. This defaults to 160 * the first child, but if there are two children becomes the bigger 161 * of the two. 162 */ 163 diff_t compareIndex = 2 * position + 1; 164 165 /* If two children exist, we only change the compare index if the 166 * second child is bigger. 167 */ 168 if (2 * position + 2 < kNumElems && 169 comp(begin[2 * position + 1], begin[2 * position + 2])) 170 compareIndex = 2 * position + 2; 171 172 /* If we're bigger than the bigger child, we're done. */ 173 if (comp(begin[compareIndex], begin[position])) 174 break; 175 176 /* Otherwise, swap with the child and continue. */ 177 std::swap(begin[compareIndex], begin[position]); 178 position = compareIndex; 179 } 180 } 181 } 182 183 /* The actual Heapsort implementation is rather straightforward - we just keep 184 * HeapInserting until we get everything, then repeatedly HeapRemove the 185 * max element. 186 */ 187 template <typename RandomIterator, typename Comparator> 188 void Heapsort(RandomIterator begin, RandomIterator end, Comparator comp) { 189 /* If the range is empty or a singleton, there is nothing to do. */ 190 if (begin == end || begin + 1 == end) 191 return; 192 193 /* Heapify the range. This works by building a forest of singleton 194 * max-heaps out of the final elements of the range, then joining 195 * them together with more and more elements. Alternatively, this 196 * can be viewed as calling HeapJoin on all suffixes of the range. 197 */ 198 for (RandomIterator itr = end; itr != begin; --itr) 199 heapsort_detail::HeapJoin(begin, itr - 1, end, comp); 200 201 /* Now, break down the heap. We continuously move the last element 202 * of the heap into the last open position, then restore the heap 203 * balance by bubbling down the last element of the heap. 204 */ 205 for (RandomIterator itr = end - 1; itr != begin; --itr) { 206 std::iter_swap(begin, itr); 207 heapsort_detail::HeapJoin(begin, begin, itr, comp); 208 } 209 } 210 211 /* The default comparator version of Heapsort just uses the default 212 * comparator on elements. The hackery with std::iterator_traits 213 * is necessary to recover the underlying iterator type. 214 */ 215 template <typename RandomIterator> 216 void Heapsort(RandomIterator begin, RandomIterator end) { 217 Heapsort(begin, end, 218 std::less<typename std::iterator_traits<RandomIterator>::value_type>()); 219 } 220 221 #endif
最新堆排序代码:
1 #include <stdio.h> 2 #include <stdlib.h> 3 #include <conio.h> 4 void AdjustUp(int a[], int k)//采用上浮的方式进行堆有序化 5 { 6 while(k > 1 && a[k/2] < a[k]) 7 { 8 int temp = a[k/2]; 9 a[k/2] = a[k]; 10 a[k] = temp; 11 12 k = k/2; 13 } 14 15 /* a[0] = a[k]; 16 int i = k/2; 17 while(i > 0 && a[i] < a[0]) 18 { 19 a[k] = a[i]; 20 k = i; 21 i = k/2; 22 } 23 a[k] = a[0];*/ 24 } 25 void BuildMaxHeap(int a[], int n)//创建大项堆 26 { 27 int i = 0; 28 for(i = n; i > n/2; i--) 29 { 30 AdjustUp(a, i); 31 } 32 } 33 void AdjustDown(int a[], int k, int len) 34 { 35 int temp; int i; 36 temp = a[k]; 37 38 for(i = 2*k; i <= len; i = i*2) 39 { 40 if(i < len && a[i] < a[i+1]) 41 { 42 i++; 43 } 44 if(temp > a[i]) 45 { 46 break; 47 } 48 else{ 49 a[k] = a[i]; 50 k = i; 51 } 52 } 53 a[k] = temp; 54 } 55 void main() 56 { 57 int a[] = {2, 87, 45, 78, 32, 17, 65, 53, 9, 63}; 58 int i = 0, j = 0; 59 BuildMaxHeap(a, 9);//构建好大项堆,堆顶元素为最大 60 for(j =1; j <= 9; j++) 61 { 62 printf("%d ", a[j]); 63 } 64 printf(" "); 65 66 for(i = 9; i > 1; i--) 67 { 68 int tmp = a[1]; 69 a[1] = a[i]; 70 a[i] = tmp; //将堆顶的最大元素与最后一个元素交换,此时堆的最后一个元素最大 71 AdjustDown(a, 1, i-1);//对剩下1~8个元素重新由上而下进行堆有序化,使得堆顶元素为最大,下次循环时交换到该堆的倒数第二位,然后依此类推 72 } 73 for(j =1; j <= 9; j++) 74 { 75 printf("%d ", a[j]); 76 } 77 getch(); 78 }
归并排序:
wiki上面的给出的算法描述:
算法描述[编辑]
归并操作的过程如下:
- 申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列
- 设定两个指针,最初位置分别为两个已经排序序列的起始位置
- 比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置
- 重复步骤3直到某一指针达到序列尾
- 将另一序列剩下的所有元素直接复制到合并序列尾
//Merging Sort
//基本思想:假设初始序列含有n个记录,则可以看成是n个有序的子序列,每个子序列的长度
//为1,然后两两归并,得到n/2的向上取整个长度为2或1的有序子序列;再两两归并。。。
//如此重复,直至得到一个长度为n的有序序列为止,这种排序方法称为2路排序算法。
//此处只讨论2路归并即两两归并
//对顺序表L作归并排序

1 void MergeSort(SqList *L) 2 { 3 MSort(L->r,L->r,1,L->length); 4 } 5 //将SR[s...t]归并排序为TR1[s...t] 6 void MSort(int SR[], int TR1[], int s, int t) 7 { 8 int m; 9 int TR2[MAXSIZE+1]; 10 if(s==t) 11 TR1[s] = sr[s]; 12 else 13 { 14 m = (s+t)/2;//将序列平分 15 MSort(SR,TR2,s,m); 16 MSort(SR,TR2,m+1,t); //递归调用MSort函数将序列不断地分成子序列 17 Merge(TR2,TR1,s,m,t); 18 } 19 }
下面采用图解来分析程序:原始序列为SR,首先将其分为两个子序列TR2,然后递归调用MSort继续对子序列划分(split)
全部化为单个子序列后再两两归并,进行排序。



1 //将有序的SR[i..m]和SR[m+1..n]归并为有序的TR[i..n] 2 void Merge(int SR[], int TR[], int i, int m, int n) 3 { 4 int j, k, l; 5 for(j=m+1,k=i;i<=m && j<=n;k++) 6 { 7 if(SR[i] < SR[j]) 8 TR[k] = SR[i++]; 9 else 10 TR[k] = SR[j++]; 11 } 12 if(i <= m) 13 { 14 for(l=0;l<=m-i;l++) 15 { 16 TR[k+1] = SR[i+l]; 17 } 18 } 19 if(j <= n) 20 { 21 for(l=0;l<=n-j;l++) 22 { 23 TR[k+l] = SR[j+l]; 24 } 25 } 26 27 }
原理很好理解:首先要根据上图所示将原始序列由1分2,2分4,依次分解下去直到分解为单个元素:程序中for循环体语句原始序列分解成的两个子序列逐个元素进行比较,依次将较小的放入新序列TR2中,然后当其中任意序列全部放入TR2中之后,再将另一序列剩余元素添加到TR2后面,这也就是后面两个if语句体所做的事情
最后附上main()函数
static void Main(string[] args) { int[] x = { 6, 2, 4, 1, 5, 9 }; int[] sorted = new int[x.Length]; merge_sort(x, 0, x.Length, sorted); for (int i = 0; i < sorted.Length; i++) ptintf (“%d”, sorted[i]); }
由归并排序结构上的递归调用联想到算法中的分治法:即将原问题划分为n个规模较小而结构与原问题相似的子问题;
递归的解决这些子问题,然后再合并其结果,就得到了原问题的解。
分治模式在每一层递归上都有三个步骤:分解(Divide),解决(Conquer),合并(Combine)。而上述归并排序的
算法完全依照了上述模式:具体分析见算法导论第二章,以下附上归并排序的伪码:

1 MERGE(A, p, q, r) 2 n1<-- q-p+1 3 n2<--r-q 4 create arrays L[1...n1+1] and R[1...n2+1] 5 for i <-- 1 to n1 6 do L[i] <-- A[p+i-1] 7 for j <-- 1 to n2 8 do R[j] <-- A[q+j] 9 L[n1+1] <-- @ 10 R[n2+1] <-- @ 11 i <-- 1 12 j <-- 1 13 for k <-- p to r 14 do if L[i] <= R[j] 15 then A[k] <-- L[i] 16 i <-- i+1 17 else A[k] <-- R[j] 18 j <-- j+1
该算法使用python实现非常简单(2路归并)
1 def merge(l1,l2): 2 final=[] 3 #对l1,l2进行排序 4 l1 = sorted(l1) 5 l2 = sorted(l2) 6 while l1 and l2: 7 if l1[0]<=l2[0]: 8 final.append(l1.pop(0)) 9 else: 10 final.append(l2.pop(0)) 11 return final+l1+l2
计数排序
原理:
Counting sort (sometimes referred to as ultra sort or math sort[1]) is a sorting algorithm which (like bucket sort) takes advantage of knowing the range of the numbers in the array to be sorted (array A). It uses this range to create an array C of this length. Each index i in array C is then used to count how many elements in A have the value i; then counts stored in C can then be used to put the elements in A into their right position in the resulting sorted array. The algorithm was created by Harold H. Seward in 1954.
计数排序是一个类似于桶排序的排序算法,其优势是对已知数量范围的数组进行排序。它创建一个长度为这个数据范围的数组C,C中每个元素记录要排序数组中对应记录的出现个数。这个算法于1954年由 Harold H. Seward 提出。
下面以示例来说明这个算法
假设要排序的数组为 A = {1,0,3,1,0,1,1}
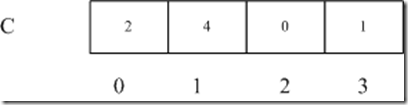
这里最大值为3,最小值为0,那么我们创建一个数组C,长度为4.
然后一趟扫描数组A,得到A中各个元素的总数,并保持到数组C的对应单元中。
比如0 的出现次数为2次,则 C[0] = 2;1 的出现次数为4次,则C[1] = 4
由于C 是以A的元素为下标的,所以这样一做,A中的元素在C中自然就成为有序的了,这里我们可以知道 顺序为 0,1,3 (2 的计数为0)
然后我们把这个在C中的记录按每个元素的计数展开到输出数组B中,排序就完成了。
也就是 B[0] 到 B[1] 为0 B[2] 到 B[5] 为1 这样依此类推。
这种排序算法,依靠一个辅助数组来实现,不基于比较,算法复杂度为 O(n) ,但由于要一个辅助数组C,所以空间复杂度要大一些,由于计算机的内存有限,这种算法不适合范围很大的数的排序。
注:基于比较的排序算法的最佳平均时间复杂度为 O(nlogn)
Counting sort
Depends on a key assumption: numbers to be sorted are integers in{0, 1, . . . , k}.
Input: A[1 . . n], where A[ j ] ∈ {0, 1, . . . , k} for j = 1, 2, . . . , n. Array A and
values n and k are given as parameters.
Output: B[1 . . n], sorted. B is assumed to be already allocated and is given as a
parameter.
Auxiliary storage: C[0 . . k]
8-4 Lecture Notes for Chapter 8: Sorting in Linear Time
COUNTING-SORT(A, B, n, k)
for i ← 0 to k
do C[i ] ← 0
for j ← 1 to n
do C[A[ j ]] ← C[A[ j ]] + 1
for i ← 1 to k
do C[i ] ← C[i ] + C[i − 1]
for j ← n downto 1
do B[C[A[ j ]]] ← A[ j ]
C[A[ j ]] ← C[A[ j ]] − 1
Do an example for A = 21, 51, 31, 01, 22, 32, 02, 33
Counting sort is stable (keys with same value appear in same order in output as
they did in input) because of how the last loop works.
//计数排序,L[n]不参与排序 void CountingSort( int L[], const int n ) { int i,j; const int k =1001;//此处k的大小只要保证大于L[]中的最大值即可 int tmp[k]; int *R; R = new int[n]; for(i=0;i<k;i++) tmp[i]= 0; for(j=0;j<n;j++) tmp[L[j]]++; //执行完上面的循环后,tmp[i]的值是L中等于i的元素的个数 for(i=1;i<k;i++) tmp[i]=tmp[i]+tmp[i-1]; //执行完上面的循环后, //tmp[i]的值是L中小于等于i的元素的个数 for(j=n-1;j>=0;j--) //这里是逆向遍历,保证了排序的稳定性 { R[tmp[L[j]]-1] = L[j]; //L[j]存放在输出数组R的第tmp[L[j]]个位置上 tmp[L[j]]--; //tmp[L[j]]表示L中剩余的元素中小于等于L[j]的元素的个数 } for(j=0;j<n;j++) L[j] = R[j]; }