Tree

1、Binary search Tree

结点的度(degree)：结点拥有的子树数；度为0的称为叶子结点；树的度是树内各节点的度的最大值；

结点的层次(Level)从根开始定义起，根为第一层，树的结点的最大层次称为树的深度(Depth)或高度;

森林(Forest)是m(m>=0)棵互不相交的树的集合；

二叉树的每个结点至多只有二棵子树(不存在度大于2的结点)，二叉树的子树有左右之分，次序不能颠倒。性质：1、二叉树的第i层至多有个结点；2、深度为k的二叉树至多有个结点；3、对任何一棵二叉树T，如果其终端结点数为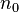，度为2的结点数为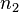，则。

特殊的二叉树：1、斜树(即线性表结构)；2、满二叉树；3、完全二叉树

树和二叉树的三个主要差别：

1. 树的结点个数至少为1，而二叉树的结点个数可以为0；
2. 树中结点的最大度数没有限制，而二叉树结点的最大度数为2；
3. 树的结点无左、右之分，而二叉树的结点有左、右之分。

<完全二叉树和满二叉树>

1. 满二叉树：一棵深度为k，且有个节点成为满二叉树
2. 完全二叉树：深度为k，有n个节点的二叉树，当且仅当其每一个节点都与深度为k的满二叉树中序号为1至n的节点对应时，称之为完全二叉树

完全二叉树的所有结点与同样深度的满二叉树，他们按层序编号的结点是一一对应的；

完全二叉树的特点：1、叶子结点只能出现在最下两层；2、如果结点度为1，则该节点只有左孩子，不存在只有右子树的情况；

 二叉树的存储结构：

1、顺序存储：二叉树可以用数组或线性表来存储，而且如果这是完全二叉树，这种方法不会浪费空间。用这种紧凑排列，如果一个结点的索引为i，它的子结点能在索引2i+1和2i+2找到，并且它的父节点（如果有）能在索引floor((i-1)/2)找到（假设根节点的索引为0）。这种方法更有利于紧凑存储和更好的访问的局部性，特别是在前序遍历中。然而，它需要连续的存储空间，这样在存储高度为h的n个结点组成的一般普通树时将会浪费很多空间。一种最极坏的情况下如果深度为h的二叉树每个节点只有右孩子需要占用2的h次幂减1，而实际却只有h个结点，空间的浪费太大，这是顺序存储结构的一大缺点。