首先这个切面把长方体切割成了两部分,显然要去考虑最小割。
如果没有光滑度的限制,把点看成边,直接建一个立体图,跑最小割即可。
加上这个限制后,带来的不同就是,如果两个点,|f(x1,y1)-f(x2,y2)|>=d,这两条边即使被割掉了,s和t依然要保证连通性不受影响。
考虑用连inf边来解决这个问题。注意想清楚连边的方向。
如果是由底层向上层连边的话,会导致如果反着走的话,及时采取了正确的割边方案,st依然会联通。
考虑反向连边,即由高层向底层。首先这样连显然不会产生刚才那种玄学情况。而且这样也确实满足了合法的割边,st一定不连通。非法的割边一定st不受影响。
例如下图:
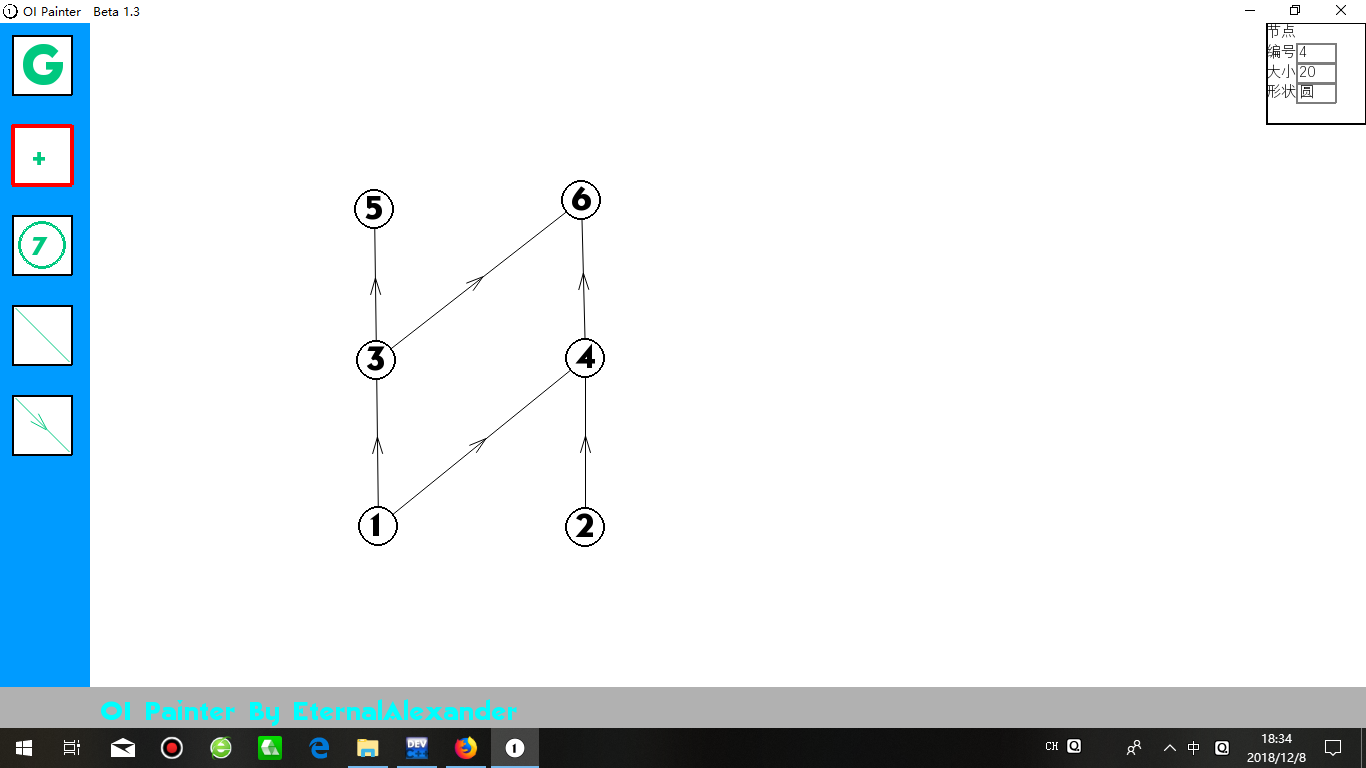
在上图中,割掉2->4和3->5也是合法的方案,然而3->6这条边的存在依然影响着s-t连通性。
#include<iostream>
#include<cctype>
#include<cstdio>
#include<cstring>
#include<string>
#include<cmath>
#include<ctime>
#include<queue>
#include<cstdlib>
#include<algorithm>
#define N 110000
#define M 440000
#define eps 1e-7
#define inf 1e9+7
#define ll long long
using namespace std;
inline int read()
{
char ch=0;
int x=0,flag=1;
while(!isdigit(ch)){ch=getchar();if(ch=='-')flag=-1;}
while(isdigit(ch)){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();}
return x*flag;
}
struct edge
{
int to,nxt,w;
}e[M];
int num,head[N];
inline void add(int x,int y,int z)
{
e[++num]=(edge){y,head[x],z};head[x]=num;
e[++num]=(edge){x,head[y],0};head[y]=num;
}
queue<int>q;
int n,m,s,t,cur[N],dep[N];
bool bfs()
{
for(int i=0;i<=t;i++)dep[i]=0,cur[i]=head[i];
dep[s]=1;q.push(s);
while(!q.empty())
{
int x=q.front();
q.pop();
for(int i=head[x];i!=-1;i=e[i].nxt)
{
int to=e[i].to;
if(!dep[to]&&e[i].w)
{
dep[to]=dep[x]+1;
q.push(to);
}
}
}
return dep[t];
}
int dfs(int x,int flow)
{
if(x==t)return flow;
for(int i=cur[x];i!=-1;i=e[i].nxt)
{
cur[x]=i;
int to=e[i].to;
if(dep[to]==dep[x]+1&&e[i].w)
{
int w=dfs(to,min(flow,e[i].w));
if(w)
{
e[i].w-=w;
e[i^1].w+=w;
return w;
}
}
}
return 0;
}
int dinic()
{
int maxflow=0;
while(bfs())maxflow+=dfs(s,inf);
return maxflow;
}
int times,id[50][50][50];
int main()
{
int a=read(),b=read(),c=read(),d=read();
num=-1;memset(head,-1,sizeof(head));
for(int k=0;k<=c;k++)
for(int i=1;i<=a;i++)
for(int j=1;j<=b;j++)
id[k][i][j]=++times;
for(int k=1;k<=c;k++)
for(int i=1;i<=a;i++)
for(int j=1;j<=b;j++)
{
add(id[k-1][i][j],id[k][i][j],read());
if(k+d<=c)
{
if(i!=1)add(id[k+d][i-1][j],id[k][i][j],inf);
if(i!=a)add(id[k+d][i+1][j],id[k][i][j],inf);
if(j!=1)add(id[k+d][i][j-1],id[k][i][j],inf);
if(j!=b)add(id[k+d][i][j+1],id[k][i][j],inf);
}
}
s=times+1;t=times+2;
for(int i=1;i<=a;i++)
for(int j=1;j<=b;j++)
{
add(s,id[0][i][j],inf);
add(id[c][i][j],t,inf);
}
printf("%d
",dinic());
return 0;
}