AC自动机的基本流程
先用所有模式串建立一颗Trie树
然后去计算Trie树每一个节点的fail指针(失配后应该转移到哪个节点)
同时额外补一些边,把Trie树改为Trie图

建立AC自动机的代码
解释一下这个补边是什么操作
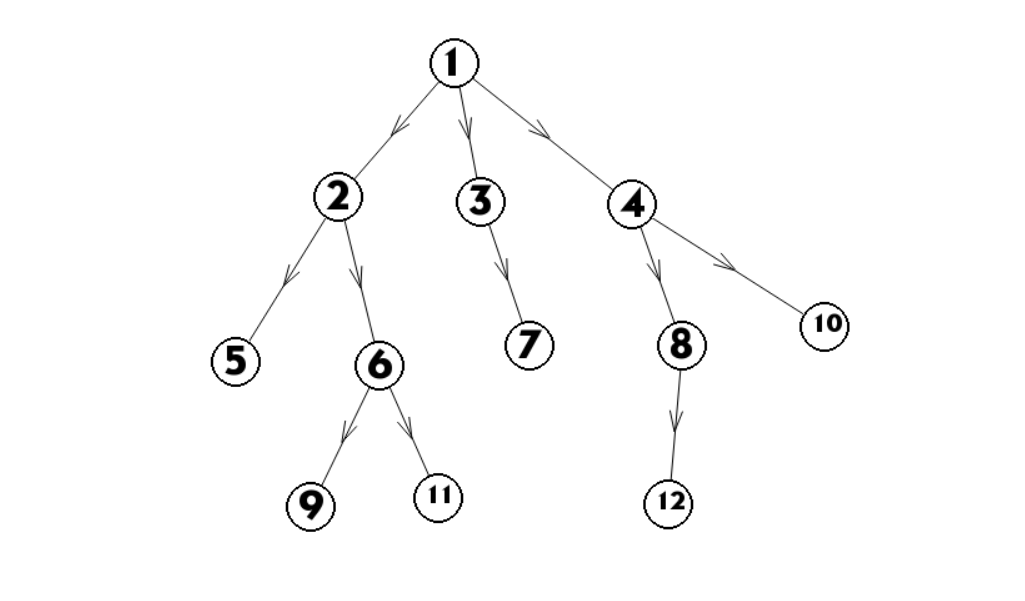
比如这棵Trie树
先考虑没有额外补边的情况
如果在9号节点尝试沿着k边走,发现nxt[x][k]为空
那么我们为了能找到一个能匹配的位置
我们只能沿着fail指针回跳,去寻找一个nxt[x][k]不为空的节点
这个回跳的过程复杂度并不太可以均摊,导致匹配的复杂度有些问题
为了优化这一点
其实也就是我们需要对于每个节点快速定位出他的第一个nxt[pa][k]不为空的祖先(指fail树上的祖先)
所以引入了额外边这个方法
其实很简单就是我们把那些nxt[x][k]为空的节点直接指向他祖先的nxt[pa][k]
计算的时候可以简单的利用nxt[x][k]=nxt[f[x]][k]来实现(有点递推的感觉)
感觉这个技巧和路径压缩是有些类似的
根据这种方法构建的Trie图,显然每一个节点的所有nxt[x][k]都是非空的
听说有的时候不能去建这个Trie图,必须只有Trie图
那也好办,只需要把额外边换一个数组来储存即可。