模拟退火求TSP问题的近似解

玻尔兹曼分布

[P_T(X = i) = frac{e^{-frac{E(i)}{KT}}}{sum_{jin S}e^{-frac{E(j)}{KT}}}\ \E(i) 表示在i状态下的温度 \S表示所有的状态 \K表示玻尔兹曼常数 \T为材料当前的温度 ]

思路介绍

如果从高温开始非常缓慢的降温，那么粒子可以在每个温度达到平衡

当系统完全冷却的时候，最终形成一个低能状态下的晶体

Metrppolis算法

• 当材料处于温度 T 时， 如果要进行状态 i->j的转换需要满足如下条件之一
  1. E(i)<E(j)
  2. 如果 E(j)>E(i) 那么状态转换接受的概率是 (e^{frac{e(i)-e(j)}{KT}})

作用：

​ 求组合优化问题，最小值问题等

最终当T降到0时，Xi满足如下分布

[P_i^*=left{egin{aligned} frac{1}{mid{S_{min}}mid},& &x_iquadinquad S_{min}\ 0, & &其他 end{aligned} ight. ]

并且可知：

[sum_{x_iin S_{min}}P_iquad=quad1 ]

应用举例

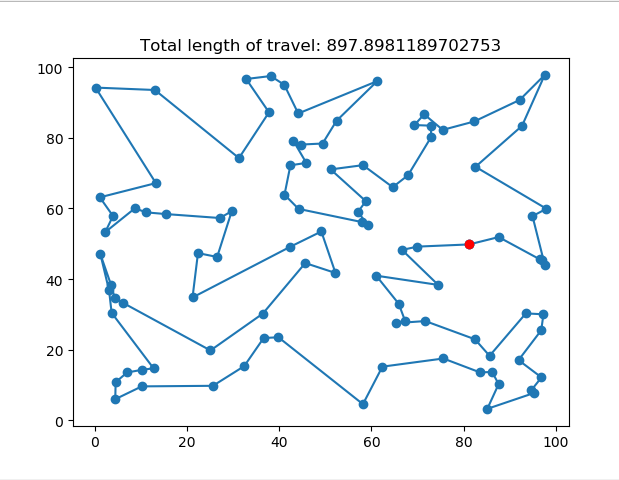
解旅行商问题

• 目标函数：

  ​ 总的距离

• 可行解：

  所有坐标点的全排列

• 变换过程

  将初始的排列的某一段反向

代码

import matplotlib.pyplot as plt
import numpy as np
import random
import math

a = np.random.rand();
point = np.random.rand(100,2)*100


#  计算每个点到每个点的距离
dist = np.zeros((100, 100), dtype=float)
for i in range(100):
	for j in range(100):
		dist[i][j] = math.sqrt((point[i][0]-point[j][0])**2 + (point[i][1]-point[j][1])**2)

# 多次随机试探求得一个相对较好的初始解
path = []
init = list(range(1,100))
length = float("inf")
for j in range(1000):
	random.shuffle(init)
	temp_len = 0
	for i in range(1,99):
		temp_len += dist[init[i-1]][init[i]]
	temp_len += dist[0][init[0]]+dist[init[98]][0]
	if temp_len<length:
		path = init[:]  #  深拷贝列表
		length = temp_len


print("init path:{}".format(path))
print("init length:{}".format(length))
cur_path = [0]
cur_path.extend(path)
cur_path.append(0)



e = 0.1**30 # 提前跳出的条件
L = 20000  # 迭代的次数
at = 0.999 # 降温速度
T = 1   #  初始的温度，忽略了K，也就是取K等于1
for t in range(L):
	# 生成一个新的路径
	# 随机数取得中间的一段， 方法是把这一段路径反向， 这样计算距离更方便
	c1, c2 = random.randint(1,99), random.randint(1,99)
	if c1>c2:
		c1, c2 = c2, c1
	df = dist[cur_path[c1]][cur_path[c2+1]]+dist[cur_path[c1-1]][cur_path[c2]]-dist[cur_path[c1-1]][cur_path[c1]]-dist[cur_path[c2]][cur_path[c2+1]]
	if df<0 or math.exp(-df/T)>random.random():
		length += df
		while c1<c2:
			cur_path[c1], cur_path[c2] = cur_path[c2],cur_path[c1]
			c1 += 1
			c2 -= 1
		T = T*at;  # 每当有接受的， 就进行降温
		if T<e:
			break;
print(cur_path)

print(point[cur_path, 0])
print(point[cur_path, 1])

plt.plot(point[cur_path, 0], point[cur_path, 1], '-o')
plt.plot(point[0][0], point[0][1], 'ro')
plt.title("Total length of travel: {}".format(length))
plt.show()
print(length)![](C:Users82504AppDataRoamingTypora	ypora-user-imagesimage-20200721093032306.png)

​