
设dp[i][j]表示以(i, j)为右下点的正方形的最大边长,则转移方程如下:
dp[i][j] = min{dp[i-1][j], dp[i][j-1], dp[i-1][j-1]} + 1 (a[i][j] == 1)
dp[i][j] = 0 (a[i][j] == 0)
转移非常简单,但是正确性却不是那么显然,考虑对于一个以(i,j)为右下点的正方形,
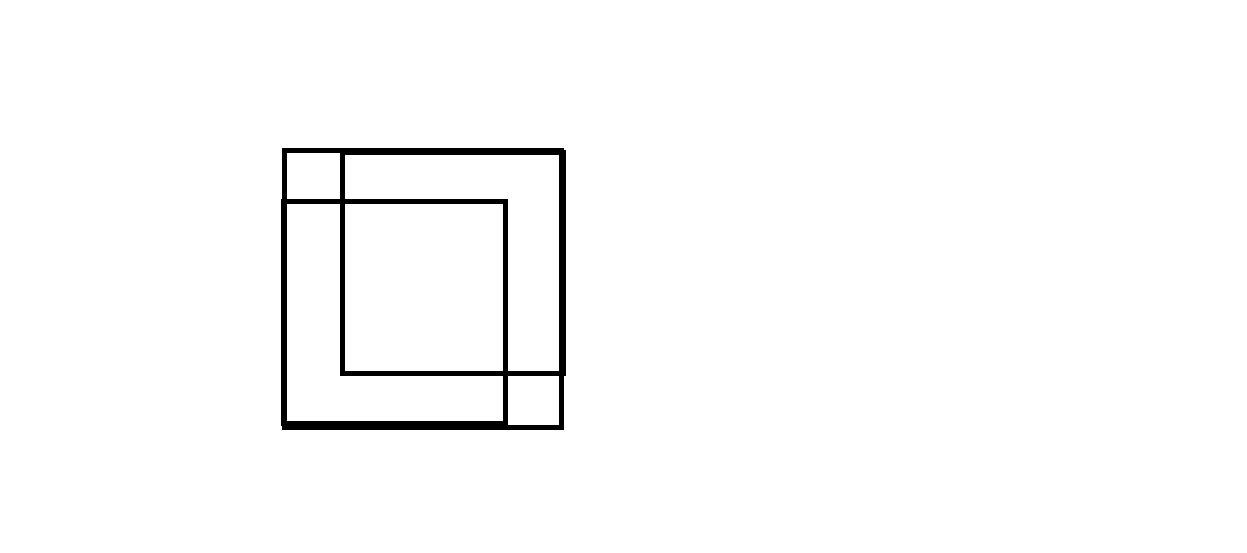
它正是由dp[i-1][j],dp[i][j-1],dp[i-1][j-1]三个正方形来限制,所以该正方形一定会满足三个正方形中最小的,可证明合法性
又可以发现,如果此时考虑的正方形边长超过了min() + 1,那么一定会与三正方形中最小的冲突,可证明最优性。
由此可推得方程
#include <cstdio>
#include <cstring>
#include <algorithm>
const int maxn = 100 + 10;
int a[maxn][maxn];
int dp[maxn][maxn];
int n, m;
int main () {
scanf("%d %d", &n, &m);
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++) scanf("%d", &a[i][j]);
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++) {
if (a[i][j] == 0) continue;
dp[i][j] = std :: min(dp[i-1][j], dp[i][j-1]);
dp[i][j] = std :: min(dp[i][j], dp[i-1][j-1]);
dp[i][j]++;
}
int ans = 0;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
if (ans < dp[i][j]) ans = dp[i][j];
printf("%d", ans);
return 0;
}