C++中的动态规划算法及常见题目汇总

什么是动态规划

• • 在面试过程中如果是求一个问题的最优解（通常是最大值或者最小值），并且该问题能够分解成若干个子问题，并且子问题之间好友重叠的更小子问题，就可以考虑用动态规划来解决这个问题。
• 动态规划的分类

　　　　　　大多数动态规划问题都可以被归类成两种类型：优化问题和组合问题

• • 优化问题

　　　　　　优化问题就是我们常见的求一个问题最优解（最大值或者最小值）

• • 组合问题　　

　　　　　　组合问题是希望你弄清楚做某事的数量或者某些事件发生的概率

• • 两种不同动态规划解决方案
    • 自上而下：即从顶端不断地分解问题，知道你看到的问题已经分解到最小并已得到解决，之后只用返回保存的答案即可
    • 自下而上：你可以直接开始解决较小的子问题，从而获得最小的解决方案。在此过程中，你需要保证在解决问题之前先解决子问题。这种方法叫做表格填充法。　　　　　　　　
• 常见的动态规划例子

1. 裴波那契数列
2. 把数字翻译成字符串
3. 最佳观光组合
4. 买卖股票的最佳时机
5. 最大子序和
6. 区域和检索-数组不可变
7. 按摩师
8. 打家劫舍
9. 最小化费爬楼梯
10. 三步问题
11. 猜数字大小

• • 　1. 裴波那契数列

　　　　　　裴波那契数列就是典型的组合问题，要求出做某事的数量或者概率

• • • 问题分析：对于题目中的青蛙爬楼梯问题，初试情况下是只有一级台阶时，只有一种跳法，只有两级台阶时，有两种跳法，当有n级台阶时，设n级台阶的跳法总数是f(n),如果第一步跳一级台阶，则和剩下的n-1级台阶的跳法是一样的，如果第一级跳两级台阶，则和剩下的n-2级台阶的跳法是一样的，因此最终n级台阶的跳法是f(n)=f(n-1)+f(n-2)，即其是可以被分解为更小的子问题的，下面我们以求解f(10)为例来分析递归的过程

                                 

　　　　　　　　我们从这张图中不难发现，在这棵树中有很多节点都是重复的，而且重复节点会随着n的增大而急剧增大，因此我们采用自顶向下的方式会有很低的效率，因此我们采用自下而上的方法，首先根据f(1)和f(2)计算出f(3),再根据f(2)和f(3计算出f(4),以此类推求出f(n)

　　　　　　　　实现的代码如下

int jumpFloor(int number) {
        if(number<0)
            return 0;
        else if(number==0||number==1||number==2)
            return number;
        else
        {
            int result=0;
            int f1=1;
            int f2=2;
            for(int i=3;i<=number;++i)
            {
                result=f1+f2;
                f1=f2;
                f2=result;
            }
            return f2;
        }
    }

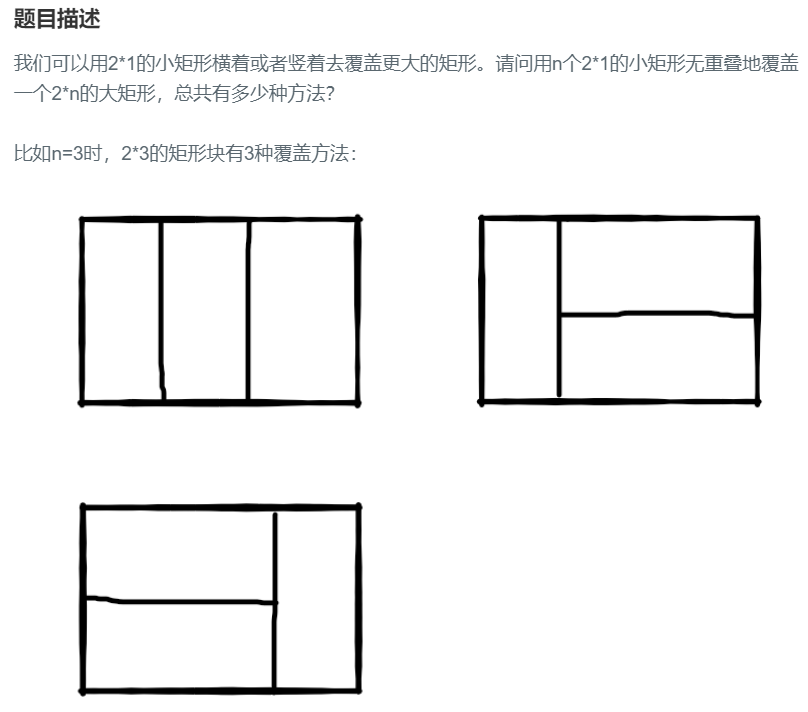
• • • 矩形覆盖问题

　　　　　　　　

• • • • 问题分析：由于2*1的小矩形可以横着放，也可以竖着放，当n=1时，其只有一种方式,f(1)=1，n=2时，有两种覆盖方式f(2)=2如图

　　　　　　　　　　

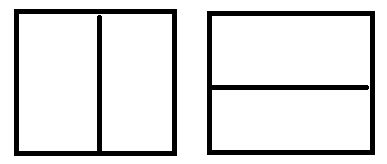
　　　　　　　　　　当要构成2*n的大矩形时，如果第一个小矩形竖着放，则其和后面n-1个小矩形的方法相等，如果第一个小矩形横着放，则第二个小矩形也只能横着放，即上图右边的方法，因此其和后面n-2个小矩形的放法相等。f(n)=f(n-1)+f(n-2)，也是一个裴波那契数列。代码如上

• • 2. 把数字翻译成字符串　

　　　　　

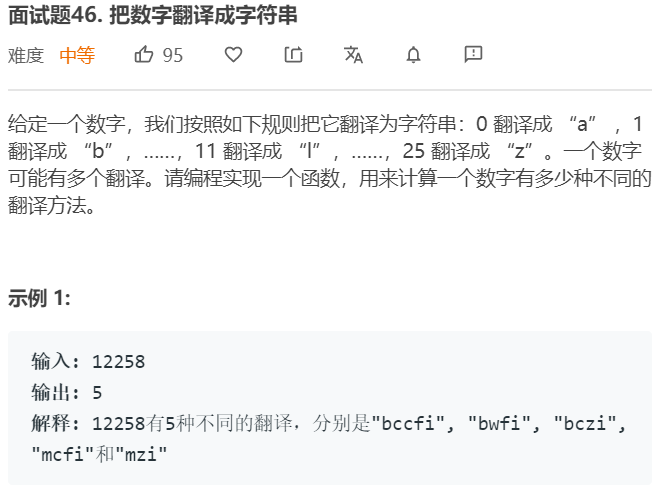
• • • 问题分析：由于是求数字的翻译方法，因此这是一个组合问题，如果对于这种数字问题，一般将其转换成字符串来进行求解，对于如果第一个位数是1，则其一定有两种解法，即可以翻译成一个数字或者两个数字，即B[i+1]=B[i]+B[i-1]，如果第一个位数是1，如果第二位数大于0，小于5，则有两种翻译方法，B[i+1]=B[i]+B[i-1]，其他情况即只有一种翻译方法：B[i+1]=B[i]
    • 我们首先看下面一个图

　　　　　　　　

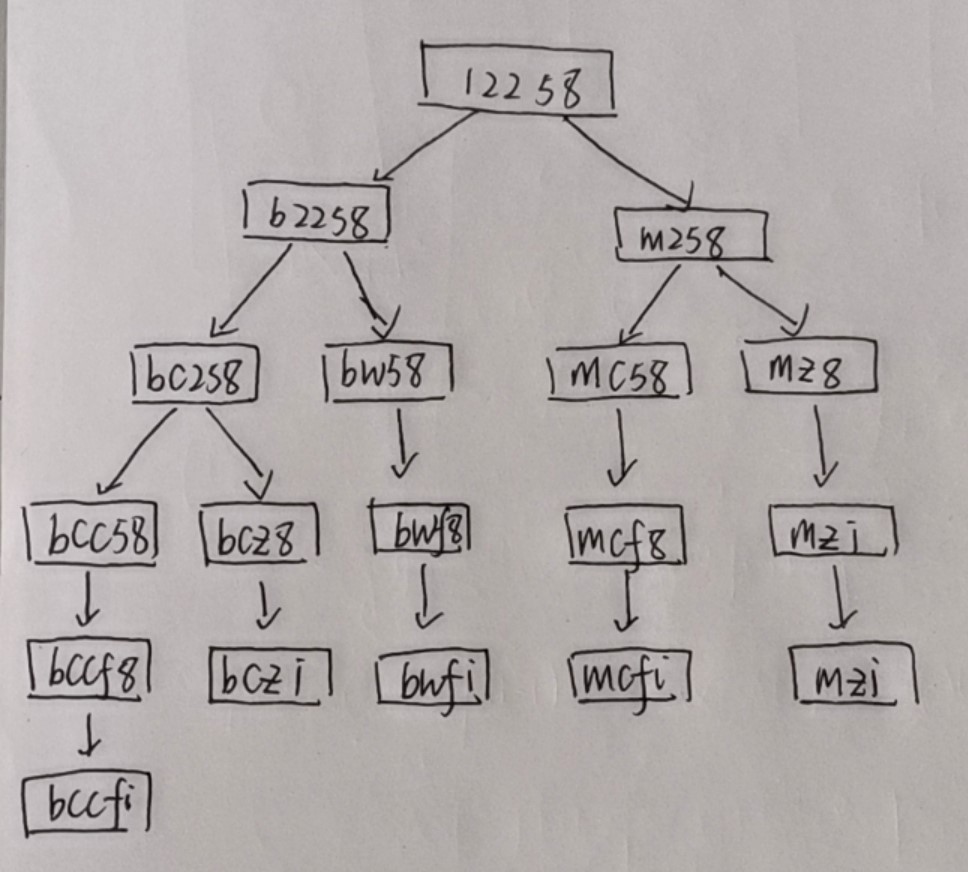
　　　　　　　　我们将一个字符串翻译分解成很多子问题来进行求解

• • • 代码参考

class Solution {
public:
    int B[70]={1,1};
    int translateNum(int num) {
        if(num<0)
            return 0;
        string nums=to_string(num);
        int numsize=nums.size();
        for(int i=1;i<numsize;++i)
        {
            if(nums[i-1]=='1')
                B[i+1]=B[i]+B[i-1];
            else if(nums[i-1]=='2')
            {
                if(nums[i]>='0'&&nums[i]<='5')
                    B[i+1]=B[i]+B[i-1];
                else
                    B[i+1]=B[i];
            }
            else
                B[i+1]=B[i];
        }
        return B[numsize];
    }
};

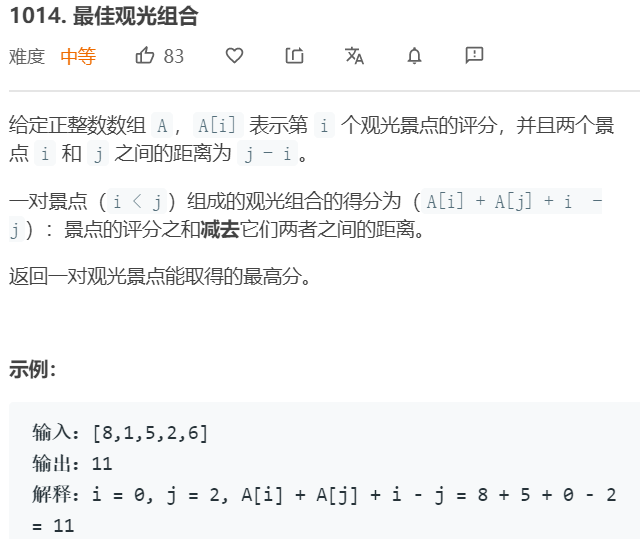
• • 3. 最佳观光组合
  • 题目描述

                

• • •  问题分析：这道题当然可以用暴力法进行求解，但是这样的时间效率过低，因此考虑其他的方法。由于两者之间的得分为A[i]+A[j]+i-j,也可以将其写成A[i]+i+A[j]-j,当遍历到j时A[j]-j的值是不变的，因此最大化A[i]+A[j]+i-j的值就等价于求[0,j-1]　

　　　　中A[i]+i的最大值mx.即景点j的答案为mx+A[j]-j，而mx的值只要从后枚举j的时候维护既可以

　　　　　　　

class Solution {
public:
    int maxScoreSightseeingPair(vector<int>& A) {
        if(A.empty())
            return 0;
        int n=A.size();
        int fn=0;
        int tn=A[0]+0;
        for(int i=1;i<n;++i)
        {
            fn=max(fn,tn+A[i]-i);
            tn=max(tn,A[i]+i);
        }
        return fn;
    }
};

　　

• • 4.  买卖股票的最佳时机
  • 题目描述

　　　　　

• • •  问题分析，由于第i天的最大收益=max[前i-1天的最大收益，第i天的最大收益]，因此其是一个动态规划问题，详细分析见下图

                     　　　　　　　　　　

• • • 代码如下

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        if(prices.empty())
            return 0;
        vector<int> result(prices.size(),0);
        int minprice=prices[0];
        for(int i=1;i<prices.size();++i)
        {
            //核心思路是，前i天的最大收益=max[前i-1天的最大收益，第i天的最大收益]
            result[i]=max(result[i-1],prices[i]-minprice);
            if(prices[i]<minprice)
                minprice=prices[i];
        }
        return result[prices.size()-1];
    }
};

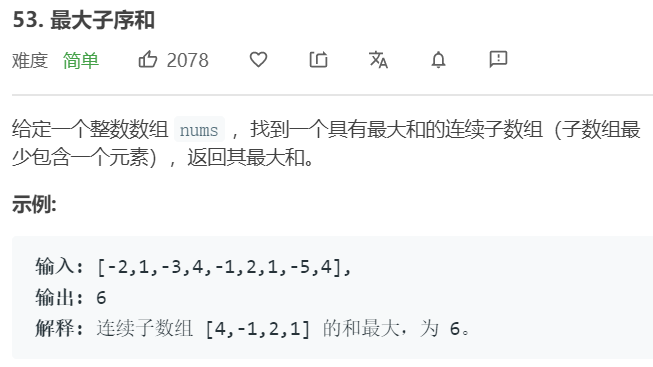
• • 5. 最大子序和
  • 题目描述

　　　　

• • • 解题分析：要找到具有最大和的连续子数组，我们有两种思路，
    • 思路一：举例分析数组的规律。从头到尾累加数组中的每个数字，初始化为0，第一步加上第一个数字，此时和为1，第二步加上第二个数字-1，此时和变成了-1；第三步加上数字3，我们注意到此前累加的和为-1，小于0，如果用-1+3，得到的和为2，小于3，也就是说，从第一个数字开始的数组和会小于第三个数字开始的子数组的和。因此，我们不用考虑从第一个数组开始的子数组，之前累加的和也被抛弃。此时我们从第三个数字开始累加，发现得到的和是3，第四步加10，得到13.。。
    • 思路二，利用动态规划的思想　　　

 　　　　　　　　

　　

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        if(nums.empty())
            return 0;
        int fn=nums[0];
        int result=nums[0];
        for(int i=1;i<nums.size();++i)
        {
            fn=max(fn+nums[i],nums[i]);
            result=max(result,fn);
        }
        return result;
    }
};

• • 6. 区域和检索，数组不可变
    • 问题描述

　　　　　　　　

• • • 解题分析：对于给定整数数组nums中，要求出数组从索引i到j范围内的总和，包含i,j两点我们可以直接求到(0-j的总和)-(0-(i-1)的总和)　　　　　　

                     

　　　　　　代码分析

class NumArray {
public:
    vector<int> res;
    NumArray(vector<int>& nums) {
        int n=nums.size();
        if(n>0)
        {
            vector<int> dp(n+1);
            dp[0]=0;
            for(int i=1;i<=n;++i)
            {
                dp[i]=dp[i-1]+nums[i-1];                
            }
            res=dp;
        }
    }  
    int sumRange(int i, int j) {
        return res[j+1]-res[i];
    }
};

/**
 * Your NumArray object will be instantiated and called as such:
 * NumArray* obj = new NumArray(nums);
 * int param_1 = obj->sumRange(i,j);
 */

• •  7. 按摩师问题
    • 题目描述

　　　　　　　　

• • • 题目分析

　　　　 　　　　　　　　

　　　　　　由于我们每一次递归，都只用到了dp[i],dp[i-1],dp[i-2]三个位置，则dp数组有点浪费，因此可以采用滚动数组的思想来进行优化

　　　　　　滚动数组实际上实在动态规划中一种节省空间的方法。由于动态规划是一个自底向上扩展的过程，我们常常需要用到的是连续的解，前面的解往往可以舍去，因此利用滚动数组优化是很有效的，利用滚动数组在N很大的情况下可以达到压缩存储的作用

                   　　　　　　　　

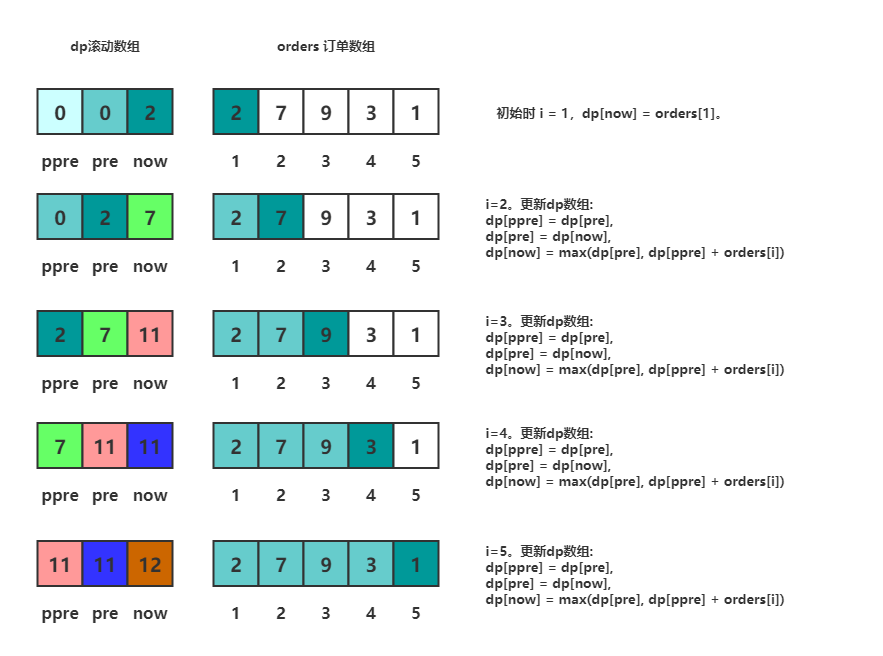
 代码

class Solution {
public:
    int massage(vector<int>& nums) {
        if(nums.empty())
            return 0;
        int ppre=0,pre=0,now=0;
        for(int i=1;i<=nums.size();++i)
        {
            ppre=pre;
            pre=now;
            now=max(pre,ppre+nums[i-1]);
        }
        return now;
    }
};

• •  8. 打家劫舍
    • 题目描述

                       

　　　　　　解法同按摩师

• • 9. 最小花费爬楼梯
    • 问题描述

                       

• • • 问题解法 　　　　

　　　            　

• • • 问题代码

class Solution {
public:
    int minCostClimbingStairs(vector<int>& cost) {
        int size=cost.size();
        vector<int> mincost(size);
        mincost[0]=0;
        mincost[1]=min(cost[0],cost[1]);
        for(int i=2;i<size;++i)
        {
            mincost[i]=min(mincost[i-1]+cost[i],mincost[i-2]+cost[i-1]);
        }
        return mincost[size-1];
    }
};

• • 10. 三步问题
    • 问题描述

                        

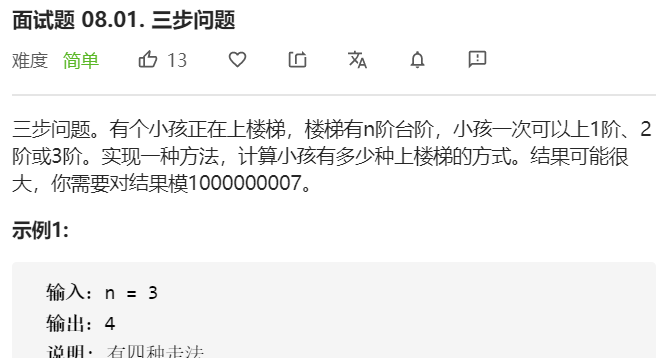
• • • 问题分析

　　　　　　　　由于每次能够走一步，两步或者三步，假设n阶台阶的总方法是f(n)，则f(1)=1,f(2)=2,f(3)=4 ,当有n级台阶的时候，如果第一级台阶走1步，则和后面的n-1级台阶一样，如果第一级台阶走2步，则和后面的n-2级台阶一样，如果第一级台阶走3步，则和后面的n-3级台阶一样，即其表达式为f(n)=f(n-1)+f(n-2)+f(n-3)，类似于裴波那契数列

                       　　

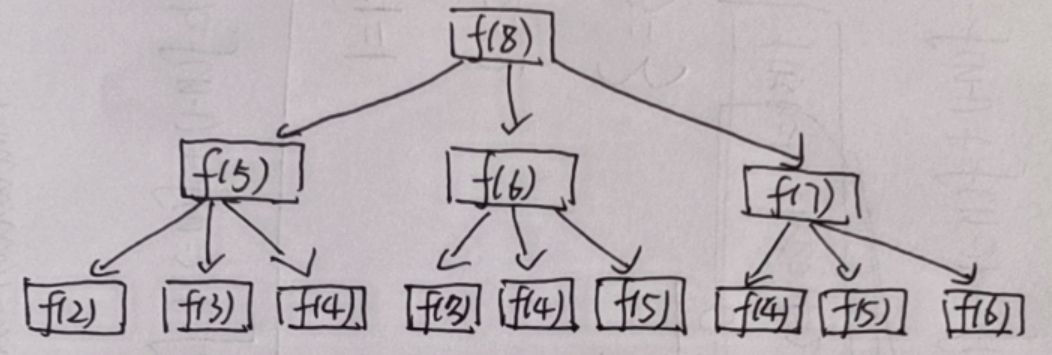
　　　　　　因此，直接调用递归会有很多重复的计算，因此我们采用自顶而下的思想进行实现

class Solution {
public:
    int waysToStep(int n) {
        if(n<3)
            return n;
        long int first=1,second=2,third=4;
        long int temp;
        while(n>3)
        {
            temp=third;
            third=(first+second+third)%1000000007;
            first=second;
            second=temp;
            --n;
        }
        return third;
    }
};

11. 猜数字大小2

• 题目描述

　　

• 解题分析

•  代码参考

class Solution {
public:
    int getMoneyAmount(int n) {
        if(n==1)
            return 0;
        //定义矩阵
        int dp[n+1][n+1];
        //初始化
        for(int i=0;i<=n;++i)
        {
            for(int j=0;j<=n;++j)
                dp[i][j]=INT_MAX;
        }
        //定义基础值dp[i][i]
        for(int i=0;i<=n;++i)
            dp[i][i]=0;
        //按列填充，从第二列开始
        for(int j=2;j<=n;++j)
        {
            //按行来，从下往上,因为填充的顺序是从下往上的
            for(int i=j-1;i>=1;--i)
            {
                //算除了两端的每一个分割点
                for(int k=i+1;k<=j-1;++k)
                {
                    dp[i][j]=min()
                }
            }

        }

    }
};