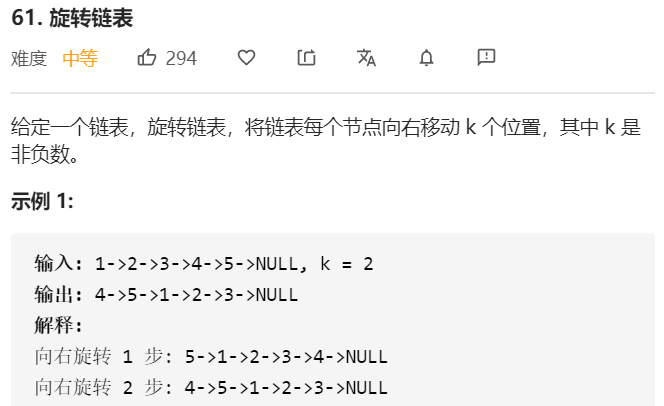
1. 二分法
二分查找也属于顺序表查找范围,二分查找也叫做折半查找,二分查找的时间效率为(logN)
二分查找的基本思想是:在有序表中,取中间记录作为比较对象,若给定值与中间记录的关键字相等,则查找成功,如果给定值小于中间值,则查找数组的前半段,否则查找数组的后半段。
二分查找只适用于有序数组或者链表
二分法常见题目汇总
一、剑指offer
二、leecode
2. 双指针法
双指针,指的是在遍历对象的过程中,不是普通的使用单个指针进行访问,而是使用两个相同的方向(快慢指针)或者相反方向(对撞指针)的指针进行扫描,从而达到相应的目的。
换言之,双指针法充分使用了数组有序这一特征,从而在某些情况下能简化一些运算。
1. 双指针法题目分析
- 面试题22: 链表中倒数第k个节点
- 删除链表中的额倒数第N个结点
- 面试题56: 删除链表中的重复节点
- 删除排序数组中的重复项
- 删除排序数组中的重复项2
- 27.移除元素
- 移动零
- 面试题5:替换空格
- 面试题61:扑克牌顺子
- 面试题02.02:返回倒数第k个节点
- 面试题10.01:合并排序的数组
- 面试题25: 合并两个排序的链表
- 比较含退格的字符
- 和为S的两数之和
- 和为S的连续正整数序列
- 三数之和
- 最接近的三数之和
- 四数之和
- 盛水最多的容器
- 链表中环的入口节点
- 旋转链表
- 回文链表
- 问题分析,由于每一行从左到右递增,每一列从上到下递增,因此我们可以考虑左下角元素,从左到右递增,从下到上递减
若需要查找的元素target等于左下角元素,则查找到,若target小于左下角元素,向上移动,若target大于左下角元素,则向右移动
- 代码参考
1 class Solution {
2 public:
3 bool Find(int target, vector<vector<int> > array) {
4 if(array.empty())
5 return 0;
6 int rows=array.size()-1;
7 int cols=0;
8 while(rows>=0&&cols<array[0].size())
9 {
10 if(target>array[rows][cols])
11 ++cols;
12 else if(target<array[rows][cols])
13 --rows;
14 else
15 return true;
16 }
17 return false;
18 }
19 };

- 问题分析
首先要搞定出旋转数组的定义,其是将一个非递减排序的数组的一个旋转,因此,旋转数组是由两个递增的子数组组成,并且第一个子数组中的元素都比第二个子数组中元素大。因此,旋转数组的最小数字一定是第二个递增子数组的头元素。因此寻找旋转数组的最小数字的方法如下:
首先设置三个指针,first指向数组头,mid指向数组中间,last指向数组尾
如果mid>first,则mid在第一个递增的子数组中,最小值在数组的后半部分
如果mid<last,则mid在第二个递增的子数组中,最小值在数组的前半部分
- 参考代码
1 class Solution {
2 public:
3 int minNumberInRotateArray(vector<int> rotateArray) {
4 int first=0;
5 int last=rotateArray.size()-1;
6 int mid=first;
7 while(rotateArray[first]>=rotateArray[last])
8 {
9 if(last-first==1)
10 {
11 mid=last;
12 break;
13 }
14 else
15 {
16 int mid=(first+last)/2;
17 if(rotateArray[first]<=rotateArray[mid])
18 first=mid;
19 else if(rotateArray[last]>=rotateArray[mid])
20 last=mid;
21 }
22 }
23 return rotateArray[mid];
24 }
25 };

- 问题分析
为了统计数字在排序数组中出现的次数,我们可利用二分法,找到第一个出现的k,再找到最后一个出现的k,即可以实现统计数字在排序数组中出现的次数
为了找到第一次出现的k,三个指针,一个指针指向数组头,一个指针指向数组尾,一个指针指向中间。如果中间指针指向的数字等于要查找的k,则判断中间指针的前一个数字是否是k,如果不是k,则找到第一个出现的k,如果是k,则第一个出现的k 在数组的前半部分。如果中间指针指向的数字小于k,则k在数组的后半部分,如果中间指针指向的数字大于k,则k在数组的前半部分
为了找到最后一次出现的k,方法是类似的,不同之处在于,如果中间指针等于k,则判断中间指针的后一个数字是否为k,如果不是k,则找到最后一个k出现的位置,否则,最后一个k出现的位置在数组的后半部分
- 参考代码
1 class Solution {
2 public:
3 //找到第一个出现的k,如果mid==k,则判断mid-1是否为k,如果为k,则第一个出现的k在数组的前半部分
4 //如果不为k,则找到第一个出现的K的位置
5 //如果mid<k,则k在数组的后半部分
6 //如果mid>k,则k在数组的前半部分
7 int getFirstk(vector<int>&data,int k,int begin,int end)
8 {
9 int mid=(begin+end)/2;
10 if(begin>end)
11 return -1;
12 else
13 {
14 mid=(begin+end)/2;
15 if(data[mid]==k)
16 {
17 if(mid==0||(mid>0&&data[mid-1]!=k))
18 return mid;
19 else
20 end=mid-1;
21 }
22 else if(data[mid]>k)
23 end=mid-1;
24 else
25 begin=mid+1;
26 return getFirstk(data,k,begin,end);
27 }
28 }
29 //找到最后一个k出现的位置
30 int getLastk(vector<int>&data,int k,int begin,int end)
31 {
32 int mid;
33 int len=data.size();
34 if(begin>end)
35 return -1;
36 else
37 {
38 mid=(begin+end)/2;
39 if(data[mid]==k)
40 {
41 if((data[mid+1]!=k&&mid<len-1)||mid==len-1)
42 return mid;
43 else
44 begin=mid+1;
45 }
46 else if(data[mid]>k)
47 end=mid-1;
48 else
49 begin=mid+1;
50 return getLastk(data,k,begin,end);
51 }
52 }
53 int GetNumberOfK(vector<int> data ,int k) {
54 if(data.empty())
55 return 0;
56 int first=0;
57 int last=data.size()-1;
58 int firstk=getFirstk(data,k,first,last);
59 int lastk=getLastk(data,k,first,last);
60 int number=0;
61 if(firstk>-1&&lastk>-1)
62 number=lastk-firstk+1;
63 return number;
64 }
65 };
二、leecode刷题
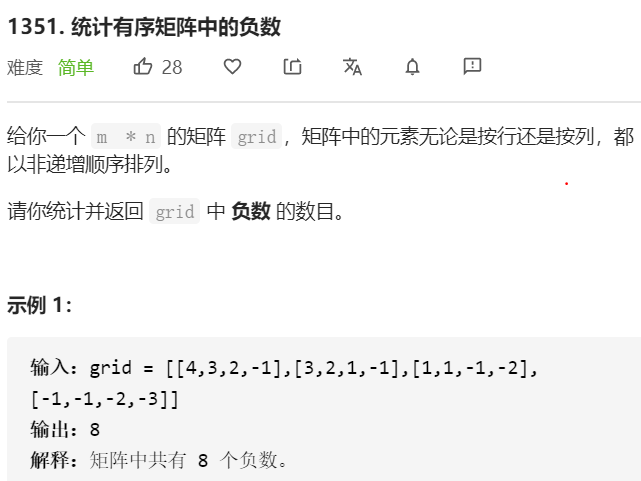
- 问题分析
这道题和前面二维数组的查找是有类似的地方的,二维矩阵从左到右非递增,从上到下非递增,对于左下角元素,从左到右递减,从下到上递增,从左下角元素开始进行扫描,如果当前元素为正,则当前元素以上的元素都比其大,因此都为正,因此向右查找;如果当前元素为负,则从当前元素开始的每一个元素都为负,统计负数的个数并且向上一排寻找
- 代码参考
1 class Solution {
2 public:
3 int countNegatives(vector<vector<int>>& grid) {
4 if(grid.empty())
5 return 0;
6 int row=grid.size()-1;
7 int col=0;
8 int number=0;
9 int rows=grid.size();
10 int cols=grid[0].size();
11 while(row>=0&&col<grid[0].size())
12 {
13 if(grid[row][col]>=0)
14 {
15 ++col;
16 continue;
17 }
18 else
19 {
20 number+=cols-col;
21 --row;
22 }
23
24 }
25 return number;
26 }
27 };
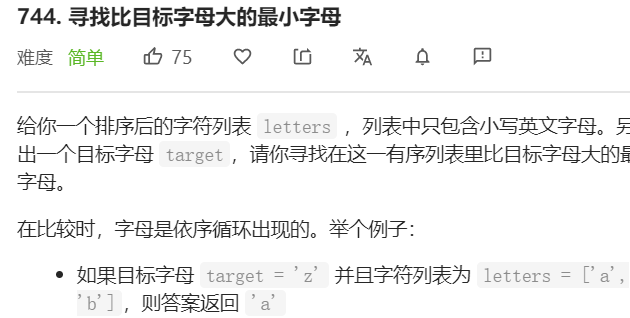
- 题目分析
要寻找比目标字母大的最小字母,采用二分法。
1. 对下标作二分,找到第一个大于target值的下标
2. target可能比letters中的所有元素都小,也可能比letters中的所有元素都大,因此第一个大于target值的下标取值范围为[0,letters.size()]
3. 当left==right时退出,因此循环条件为while(left<right)
4. 当letters[mid]>target,mid可能是结果,因此在数组的前半部分寻找
5. 当letters[mid]<=target,mid不可能是结果,直接舍弃,因此在数组的后半部分寻找
6. 当循环退出时,left==right,若target大于letters中的所有元素,left=letters.size(),此时返回letters[0]
- 参考代码
1 class Solution {
2 public:
3 char nextGreatestLetter(vector<char>& letters, char target) {
4 int left=0;
5 int right=letters.size();
6 while(left<right)
7 {
8 int mid=(left+right)/2;
9 //如果letters[mid]>target,mid是可能结果,在数组的前半部分
10 if(letters[mid]>target)
11 right=mid;
12 //如果letters[mid]<=target,mid不可能是结果,舍去,在数组后半部分
13 else
14 left=mid+1;
15 }
16 //如果target大于数组中的所有元素时,left==letters.size(),返回letters[0]
17 if(left==letters.size())
18 return letters[0];
19 else
20 return letters[left];
21 }
22 };
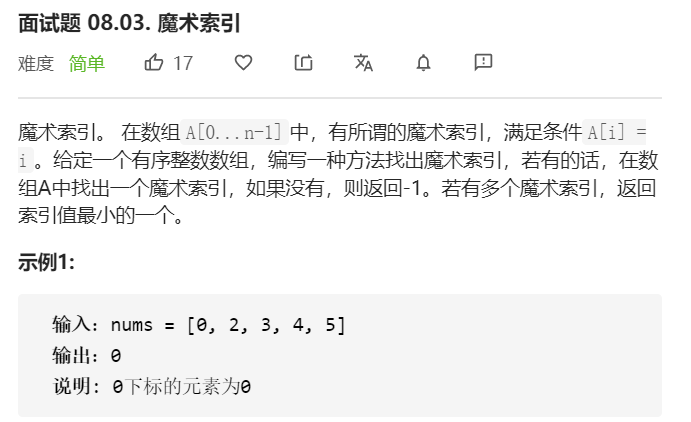
- 题目分析
对于这道题目,刚开始看到的时候会思考使用暴力法,从头到尾进行求解。但是这样做的时间效率很低,为O(n),因此尝试找其他新的方法
除了暴力法外,由于其是有序整数数组,因此我们可以思考使用二分法进行求解。
两个指针,一个指针位于数组头,一个指针位于数组尾。
如果nums[mid]==mid,则判断其是否是最小的
如果nums[mid]!=mid,则先判断左边是否有满足条件的。如果左边没有满足条件的,再判断右边是否有满足条件的。
- 参考代码
1 class Solution {
2 public:
3 int findMagicIndex(vector<int>& nums) {
4 if(nums.empty())
5 return -1;
6 return findMinMagicIndex(nums,0,nums.size()-1);
7 }
8 int findMinMagicIndex(vector<int>&nums,int left,int right)
9 {
10 int t;
11 if(left==right)
12 {
13 if(nums[left]==left)
14 return left;
15 else
16 return -1;
17 }
18 int mid=(left+right)/2;
19 if(nums[mid]==mid)
20 {
21 t=findMinMagicIndex(nums,left,mid);
22 return (t==-1)?mid:t;
23 }
24 else
25 {
26 //先从左边找,没有再从右边找
27 int t=findMinMagicIndex(nums,left,mid);
28 if(t!=-1)
29 return t;
30 else
31 return findMinMagicIndex(nums,mid+1,right);
32 }
33 }
34 };

- 题目分析
其是这是一个二分类问题,即需要找到[1,n]中的某个数,以实现这个数之前的所有和叠加小于等于n
即在一个等差数列中,找到一个位置,这个位置之前的所有元素加起来小于等于n
两个指针,一个指向数组头,一个指向数组尾,mid=l+(r-l)/2,而不写成mid=(l+r)/2的原因是:l+r可能造成溢出
cursum=mid*(mid+1)/2,
如果cursum<n,则要查找的位置在mid后面
如果cursum==n,则要查找的位置在mid处
如果cursum>n,则要查找的位置在mid后面
- 代码参考
1 class Solution {
2 public:
3 int arrangeCoins(int n) {
4 if(n<=0)
5 return 0;
6 int l=1,r=n;
7 while(l<=r)
8 {
9 long mid=l+(r-l)/2;//写成mid=(l+r)/2可能存在溢出的问题
10 long cur=mid*(mid+1)/2;
11 if(cur<n)
12 l=mid+1;
13 else if(cur==n)
14 return mid;
15 else
16 r=mid-1;
17 }
18 return l-1;
19 }
20 };

- 题目分析
首先需要保证houses和heaters都是升序的
对于每一个房子左边的暖气,记录他使其成为下一个房子左边最开始计算的暖气
对于每一个房子右边的暖气,则其为最后一个需要计算的暖气
依次为标准滑动遍历房子和暖气
- 参考代码
1 class Solution {
2 public:
3 int findRadius(vector<int>& houses, vector<int>& heaters) {
4 //首先要保证houses和heaters都是升序排列的
5 sort(houses.begin(),houses.end());
6 sort(heaters.begin(),heaters.end());
7 int ans=0;
8 int k=0;
9 for(int i=0;i<houses.size();++i)
10 {
11 int radis=INT_MAX;//先设置到最大:整型下限
12 for(int j=k;j<heaters.size();++j)
13 {
14 //如果其是左边的加热器,则记录器成为下一个房子开始的暖气
15 k=(houses[i]>=heaters[j])?j:k;
16 radis=min(radis,abs(houses[i]-heaters[j]));
17 if(houses[i]<heaters[j])
18 break;
19
20 }
21 //ans记录最大半径
22 ans=max(ans,radis);
23 }
24 return ans;
25 }
26 };

- 题目分析
由题意,版本号在某个之后全部错误,这相当于是一个排序的数组,因此我们采用二分法
两个指针,一个指针begin指向数组头,一个指针end指向数组尾,一个指针mid=begin+(end-begin)/2
如果mid指向数组是true,则错误版本在数组的后半部分
如果mid指向的数组是false,则判断其是否是第一个出现的,如果是第一个出现的,直接返回mid,否则第一个出现错误的位置在数组的前半部分
- 参考代码
1 // The API isBadVersion is defined for you.
2 // bool isBadVersion(int version);
3
4 class Solution {
5 public:
6 int firstBadVersion(int n) {
7 if(n<=0)
8 return 0;
9 int begin=1;
10 int end=n;
11 int mid;
12 int flag=0;
13 while(begin<=end)
14 {
15 mid=begin+(end-begin)/2;
16 if(!isBadVersion(mid))
17 begin=mid+1;
18 else
19 {
20 if(!isBadVersion(mid-1))
21 {
22 flag=mid;
23 break;
24 }
25
26 else
27 end=mid;
28 }
29 }
30 return flag;
31 }
32 };
- 题目分析
很明显这是一个二分查找问题,对于这类问题,我们最主要的就是要知道移动的方向以及返回的条件,我们使用一个实际例子来进行说

- 参考代码
1 class Solution {
2 public:
3 int peakIndexInMountainArray(vector<int>& A) {
4 if(A.empty())
5 return 0;
6 int begin=0;
7 int end=A.size()-1;
8 int mid;
9 while(begin<=end)
10 {
11 mid=begin+(end-begin)/2;
12 if(A[mid]>A[mid-1]&&A[mid]>A[mid+1])
13 return mid;
14 else if(A[mid-1]<A[mid]&&A[mid]<A[mid+1])
15 begin=mid+1;
16 else
17 end=mid-1;
18 }
19 return 0;
20 }
21 };

- 问题分析
其实这本质上是一个二分部查找的搜索问题,只是他是稀疏的,就要排除左边界是空字符串,右边界是空字符串以及mid是空字符串的问题
- 代码参考
1 class Solution {
2 public:
3 int findString(vector<string>& words, string s) {
4 if(words.empty())
5 return -1;
6 int begin=0;
7 int end=words.size()-1;
8 int mid;
9 while(begin<=end)
10 {
11 if(words[begin].size()==0)
12 {
13 ++begin;
14 continue;
15 }
16 if(words[end].size()==0)
17 {
18 --end;
19 continue;
20 }
21 mid=begin+(end-begin)/2;
22 while(words[mid].size()==0)
23 ++mid;
24 if(words[mid]==s)
25 return mid;
26 else if(words[mid]<s)
27 begin=mid+1;
28 else
29 end=mid-1;
30 }
31 return -1;
32 }
33 };
2. 双指针法题目分析
一、剑指offer
- 问题分析
要找到链表中的倒数第k个元素,我们可以采用双指针法,两个指针p,q刚开始都位于链表头,一个指针p先向前走k步,此时指针p,q相差k步,然后同时移动指针p,q,当指针p到达链表尾的时候,指针q到达链表的倒数第k个节点
- 代码参考
1 /**
2 * Definition for singly-linked list.
3 * struct ListNode {
4 * int val;
5 * ListNode *next;
6 * ListNode(int x) : val(x), next(NULL) {}
7 * };
8 */
9 class Solution {
10 public:
11 ListNode* getKthFromEnd(ListNode* head, int k) {
12 if(head==nullptr)
13 return nullptr;
14 ListNode* p=head;
15 ListNode* q=head;
16 int i=0;
17 while(p!=nullptr)
18 {
19 if(i<k)
20 {
21 p=p->next;
22 ++i;
23 }
24 else
25 {
26 p=p->next;
27 q=q->next;
28 }
29 }
30 return i<k?nullptr:q;
31 }
32 };
- 题目分析
这道题解法其是和找到链表中的倒数第N个结点相似,思路都是使用双指针,一个指针先向前走N步,此时两个指针间隔我们需要的数值,当一个指针到达链表尾的时候,另一个指针到达倒数第N点。
但是删除链表中的倒数第N个结点面临的一个挑战就是,当其到达倒数第N个结点时,要将倒数第N个结点删除,我们就需要找到倒数第N个结点的前一个节点,然后将前一个节点的next指针指向倒数第N个结点的下一个结点。
因此刚开始可以思考直接指向其倒数第N+1个结点,然后将N+1节点的next指针指向next->next指针,但是这样会出现的一个问题就是,若要倒数第N个结点刚好是头结点,这种删除方式就会出错。
因此我们引入了哑节点:哑节点是链表中的一个概念,哑节点是在一个链表的前边添加一个节点,存放的位置是在数据节点之前,头节点之后。好处是加入哑节点止呕可以使所有数据节点都有前驱节点,这样会方便执行链表的操作,看到一篇文章讲有无哑节点的区别,可以参考这个博客https://blog.csdn.net/muclenerd/article/details/42008855
- 参考代码
1 /** 2 * Definition for singly-linked list. 3 * struct ListNode { 4 * int val; 5 * ListNode *next; 6 * ListNode(int x) : val(x), next(NULL) {} 7 * }; 8 */ 9 class Solution { 10 public: 11 ListNode* removeNthFromEnd(ListNode* head, int n) { 12 if(head==nullptr) 13 return nullptr; 14 ListNode* dummy=new ListNode(0); 15 dummy->next=head; 16 int i=0; 17 ListNode* p=dummy; 18 ListNode* q=dummy; 19 for(int i=0;i<n;++i) 20 { 21 p=p->next; 22 } 23 while(p->next!=nullptr) 24 { 25 p=p->next; 26 q=q->next; 27 } 28 q->next=q->next->next; 29 ListNode* res=dummy->next; 30 delete dummy; 31 return res; } 32 };

- 题目分析
假设有链表如上图所示,我们可以采用双指针来实现删除链表中的重复节点,一个指针指向pHead,一个指针next指向pHead->next
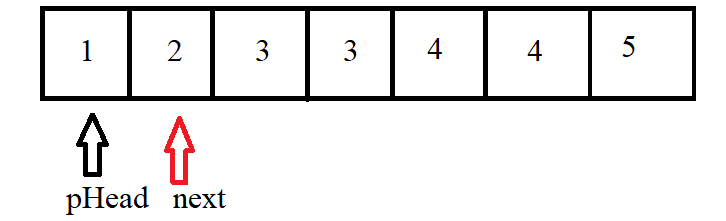
如果pHead->val==next->val,则移动next,否则则又开始递归
- 代码参考
1 /* 2 struct ListNode { 3 int val; 4 struct ListNode *next; 5 ListNode(int x) : 6 val(x), next(NULL) { 7 } 8 }; 9 */ 10 class Solution { 11 public: 12 ListNode* deleteDuplication(ListNode* pHead) 13 { 14 if(pHead==nullptr||pHead->next==nullptr) 15 return pHead; 16 ListNode* next=pHead->next; 17 if(pHead->val==next->val) 18 { 19 while(next&&pHead->val==next->val) 20 next=next->next; 21 return deleteDuplication(next); 22 } 23 else 24 { 25 pHead->next=deleteDuplication(pHead->next); 26 return pHead; 27 } 28 } 29 };

- 思路分析
要实现替换空格,由于替换空格前后字符串的长度会发生变化,因此替换空格后的字符串长度等于原始字符串长度+2*空格数,因此我们从字符串的后面开始复制和替换,首先准备两个指针,p1和p2,p1指向原始字符串的末尾,p2指向替换之后字符串的末尾,如果没有空格,则依次进行复制,碰到空格时,新的字符串依次复制入‘0’,‘2’,‘%’

- 代码参考
1 class Solution { 2 public: 3 // 替换空格后,字符串长度会发生变化,原始字符串长度为originallen, 4 /* 5 newlen=originallen+2*space 6 */ 7 void replaceSpace(char *str,int length) { 8 if(str==nullptr) 9 return; 10 //首先计算原始长度和空格的长度 11 int originallen=0; 12 int space=0; 13 int i=0; 14 while(str[i]!='�') 15 { 16 ++originallen; 17 if(str[i]==' ') 18 ++space; 19 ++i; 20 } 21 //由原始字符串长度和空格数求出新的字符串长度 22 int newlen=originallen+2*space; 23 //设置双指针,一个指向原始数组尾,一个指向申请的数组尾 24 int indexoriginal=originallen; 25 int indexnew=newlen; 26 while(indexoriginal<=indexnew&&indexoriginal>=0) 27 { 28 if(str[indexoriginal]==' ') 29 { 30 str[indexnew--]='0'; 31 str[indexnew--]='2'; 32 str[indexnew--]='%'; 33 } 34 else 35 str[indexnew--]=str[indexoriginal]; 36 --indexoriginal; 37 } 38 } 39 };
- 解题分析
大小王数特殊的数字,我们将其定义为0,以便和其他扑克牌分开
要判断扑克牌中是否是顺子,我们可以遵循如下步骤:
首先将所有数字排序
统计排序后数组中0的个数
要使得其能够成为顺子,我们只需要数组中相邻数字的间隔数>=0的个数,并且没有对子
要实现如上的判断,我们只需要设置两个指针,一个指针指向第一个不为0的数,另一个指针指向其后一个数,统计相邻数字之间的间隔数,并和0的个数进行比较
- 代码参考
1 class Solution { 2 public: 3 bool IsContinuous( vector<int> numbers ) { 4 //要实现扑克牌顺子,将大小王看成0,则0的个数>=数字之间的间隔数并且不能存在对子 5 if(numbers.empty()) 6 return false; 7 sort(numbers.begin(), numbers.end()); 8 9 int numberofzero=0; 10 int numberofgap=0; 11 //计算0的个数 12 for(int i=0;i<numbers.size()&&numbers[i]==0;++i) 13 ++numberofzero; 14 int small=numberofzero; 15 int big=small+1; 16 while(big<numbers.size()) 17 { 18 if(numbers[small]==numbers[big]) 19 return false; 20 //判断gap的总数 21 numberofgap+=numbers[big]-numbers[small]-1; 22 ++small; 23 ++big; 24 } 25 return numberofzero<numberofgap?false:true; 26 } 27 };
二、Leecode
- 问题分析
这道题和上面那道题类似
- 代码参考
1 /** 2 * Definition for singly-linked list. 3 * struct ListNode { 4 * int val; 5 * ListNode *next; 6 * ListNode(int x) : val(x), next(NULL) {} 7 * }; 8 */ 9 class Solution { 10 public: 11 int kthToLast(ListNode* head, int k) { 12 if(head==nullptr) 13 return 0; 14 ListNode* p=head; 15 ListNode* q=head; 16 int i=0; 17 while(p!=nullptr) 18 { 19 if(i<k) 20 { 21 p=p->next; 22 ++i; 23 } 24 else 25 { 26 p=p->next; 27 q=q->next; 28 } 29 } 30 return i<k?0:q->val; 31 } 32 };

- 题目分析
要实现合并排序的数组,其是要实现原地修改,因此我们应该思考从后面实现开始填充

- 代码参考
1 class Solution { 2 public: 3 void merge(vector<int>& A, int m, vector<int>& B, int n) { 4 if(A.empty()||B.empty()) 5 return; 6 int idx1=m-1; 7 int idx2=n-1; 8 int cur=m+n-1; 9 while(idx1>=0&&idx2>=0) 10 { 11 if(A[idx1]<B[idx2]) 12 { 13 A[cur]=B[idx2]; 14 --cur; 15 --idx2; 16 } 17 else 18 { 19 A[cur]=A[idx1]; 20 --cur; 21 --idx1; 22 } 23 } 24 while(idx2>=0) 25 { 26 A[cur]=B[idx2]; 27 --cur; 28 --idx2; 29 } 30 } 31 };
- 问题分析
对于这个问题,我们可以使用两个栈和双指针来进行实现,
两个栈分别存储两个字符串,双指针分别指向两个字符串,如果遇到#,则将栈顶元素弹出。
最后遍历比较两个栈,如果不同,则返回false,如果相同,则返回true
- 代码参考
1 class Solution { 2 public: 3 //思路:利用两个栈,不断向栈中添加字符,遇上#则删除栈顶元素,最后比较栈中的字符是否相同 4 bool backspaceCompare(string S, string T) { 5 if(S.empty()&&T.empty()) 6 return true; 7 stack<char> s; 8 int si=0; 9 stack<char> t; 10 int ti=0; 11 while(S[si]!='�') 12 { 13 if(S[si]=='#') 14 { 15 if(!s.empty()) 16 { 17 s.pop(); 18 } 19 } 20 else 21 { 22 s.push(S[si]); 23 } 24 ++si; 25 } 26 while(T[ti]!='�') 27 { 28 if(T[ti]=='#') 29 { 30 if(!t.empty()) 31 { 32 t.pop(); 33 } 34 } 35 else 36 { 37 t.push(T[ti]); 38 } 39 ++ti; 40 } 41 while(!s.empty()&&!t.empty()) 42 { 43 if(s.top()!=t.top()) 44 return false; 45 s.pop(); 46 t.pop(); 47 } 48 if(!s.empty()||!t.empty()) 49 return false; 50 return true; 51 } 52 };

- 问题分析
我们可以使用两个指针,一个指针指向已重新组织的元素,一个指针指向未处理的元素

- 代码参考
1 class Solution { 2 public: 3 int removeDuplicates(vector<int>& nums) { 4 if(nums.empty()) 5 return 0; 6 int cur=0; 7 int index=0; 8 int len=nums.size(); 9 while(index<len) 10 { 11 if(nums[cur]!=nums[index]) 12 { 13 nums[++cur]=nums[index]; 14 } 15 ++index; 16 } 17 return cur+1; 18 } 19 };
- 思路分析
使用两个指针:快指针和慢指针
快指针:遍历整个数组
慢指针:记录每个可以覆写的位置
题目中规定每个元素最多出现两次,因此我们可以检查快指针和慢指针的前一个元素是否相等
如果快指针和慢指针的前一个元素相等,则只移动快指针
如果快指针和慢指针的前一个元素不等,则向后移动一位慢指针,并将快指针所指向的元素写入慢指针指向的单元,最后移动快指针
- 代码参考
1 class Solution { 2 public: 3 int removeDuplicates(vector<int>& nums) { 4 int len=nums.size(); 5 if(len<=2) 6 return len; 7 int slow=1; 8 int fast=2; 9 while(fast<len) 10 { 11 if(nums[slow-1]!=nums[fast]) 12 nums[++slow]=nums[fast]; 13 ++fast; 14 } 15 return slow+1; 16 } 17 };
- 题目分析
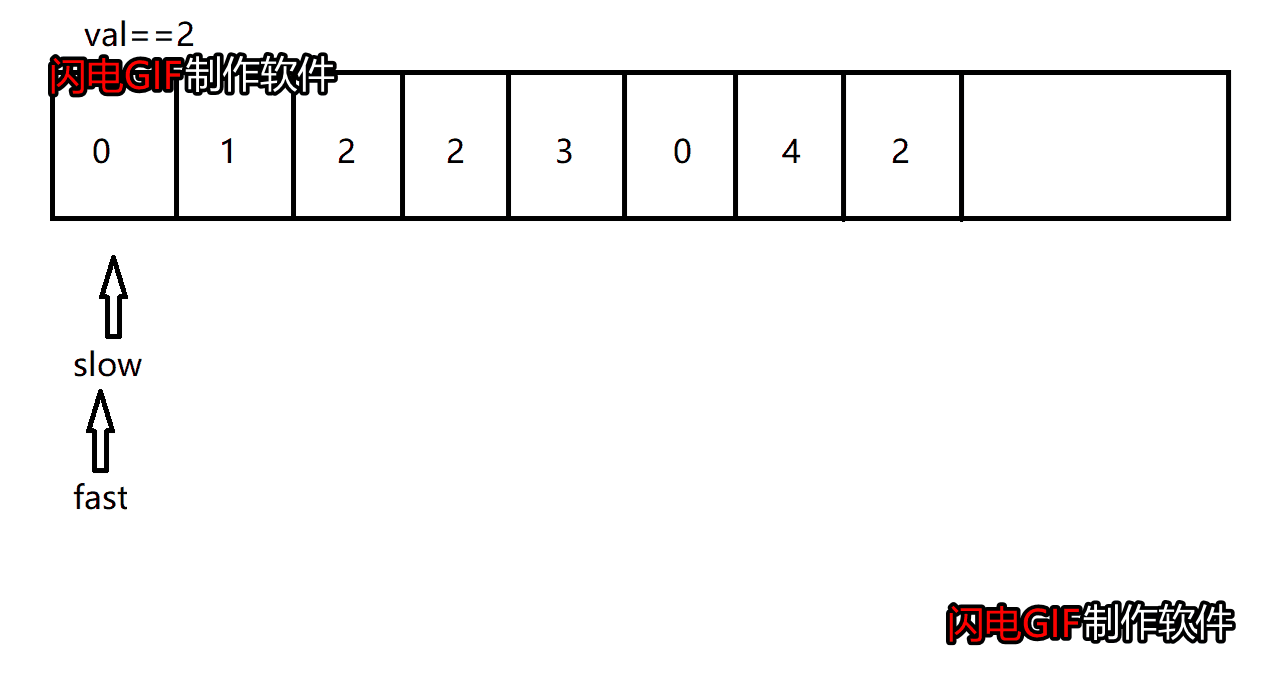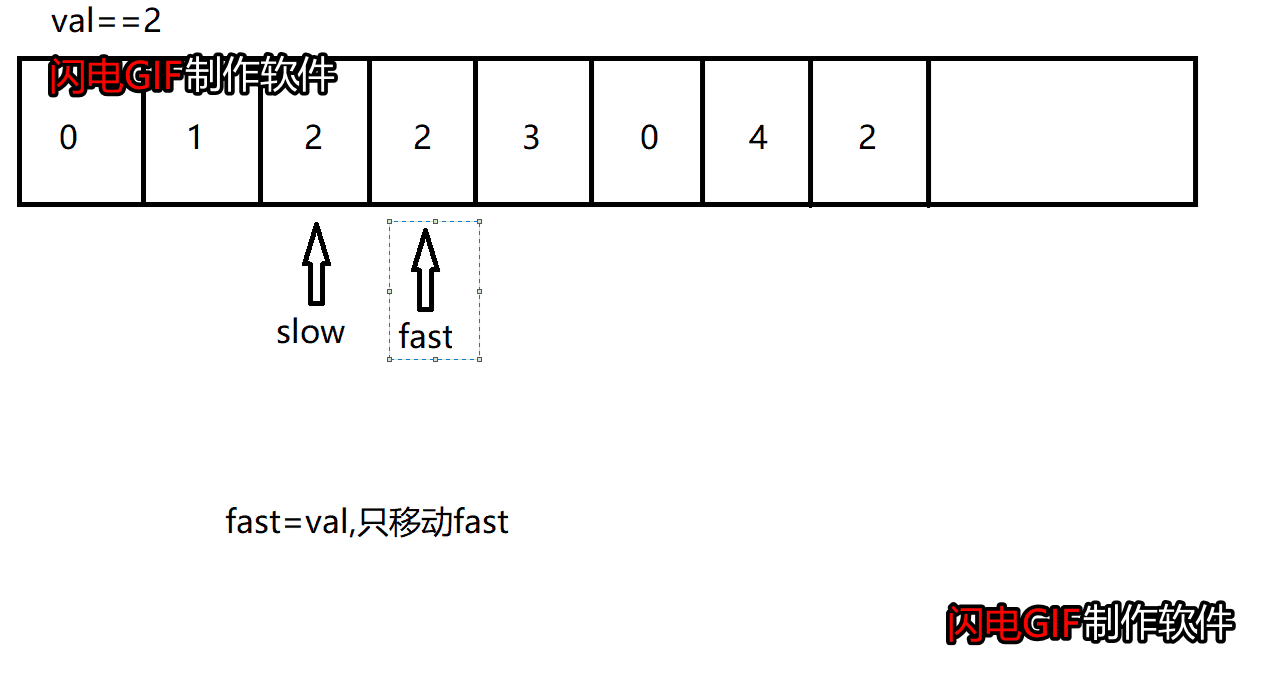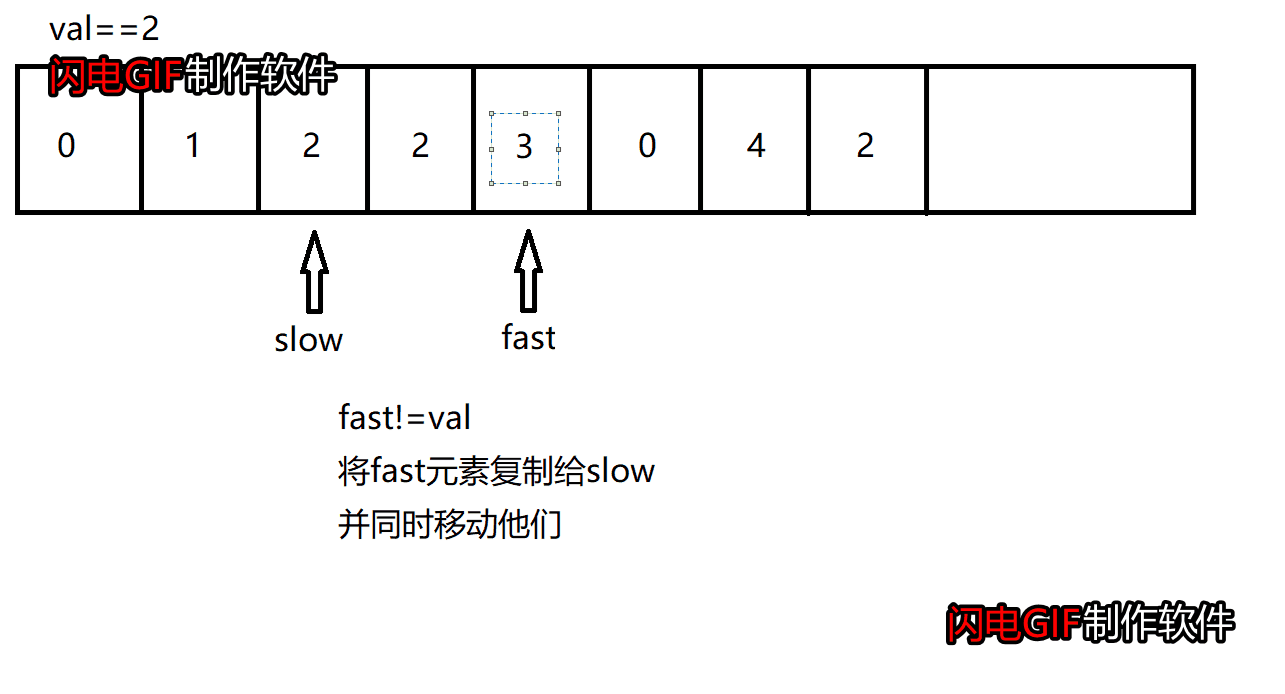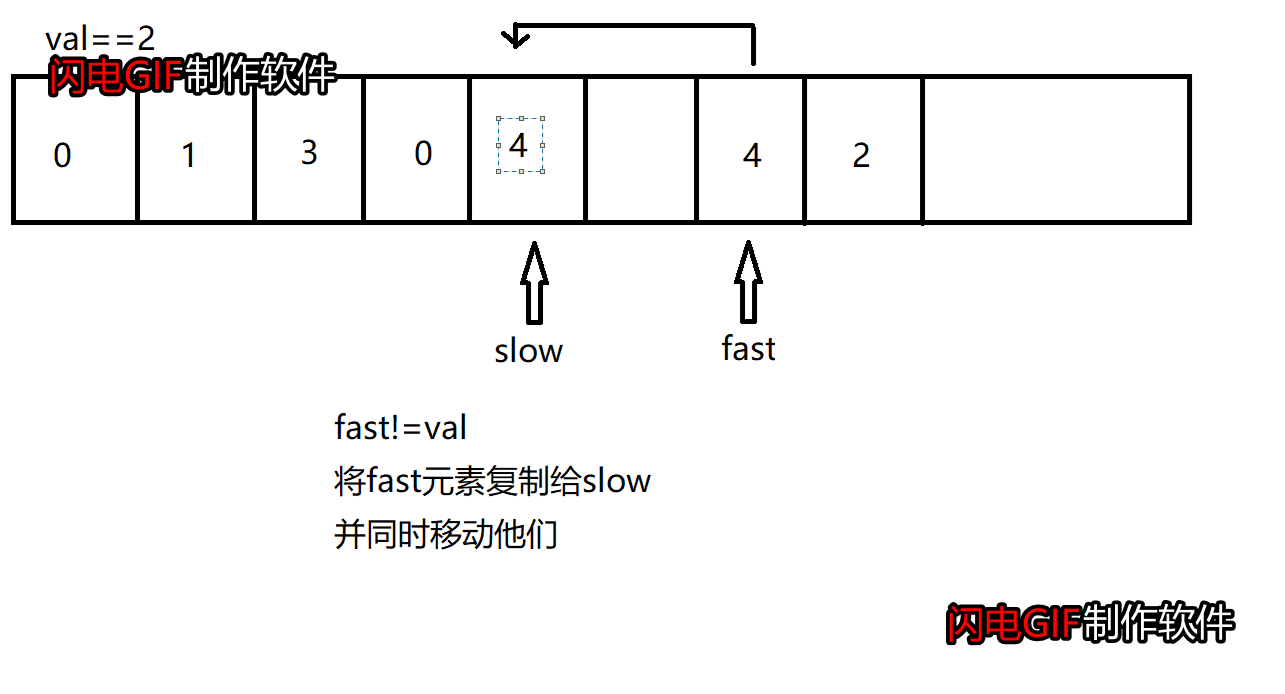
这道题和前面删除重复元素是类似的,要实现移除数组中数值等于val的元素,我们可以使用双指针:快指针和慢指针,快指针遍历整个数组,慢指针指向待操作的位置。
若快指针指向的元素等于val,则只移动快指针
若快指针指向的元素不等于val,则将快指针指向的元素赋值给慢指针,然后同时移动快指针和慢指针
- 代码参考
1 class Solution { 2 public: 3 int removeElement(vector<int>& nums, int val) { 4 int len=nums.size(); 5 if(len<=0) 6 return len; 7 //使用一个快指针和一个慢指针,快指针每次遍历整个数组,慢指针指向需要操作的位置 8 int slow=0; 9 int fast=0; 10 for(int fast=0;fast<len;++fast) 11 { 12 //如果快指针指向的元素fast=val,则只移动fast 13 //如果快指针指向的元素fast!=val,则将快指针指向的元素值复制给慢指针指向的元素值,并且同时更新快指针和慢指针 14 if(nums[fast]!=val) 15 { 16 nums[slow]=nums[fast]; 17 ++slow; 18 } 19 } 20 return slow; 21 } 22 };
- 问题分析
要实现将数组中所有0移动到数组的末尾,我们也是使用和之前移除元素类似的方法,使用双指针进行操作
双指针:快指针和慢指针,快指针遍历整个数组,慢指针指向待操作的元素。
刚开始两个指针都指向数组开头,利用快指针fast来遍历整个数组,如果fast!=0,则将fast的元素和slow的元素交换,并同时移动fast和slow,否则,只移动fast
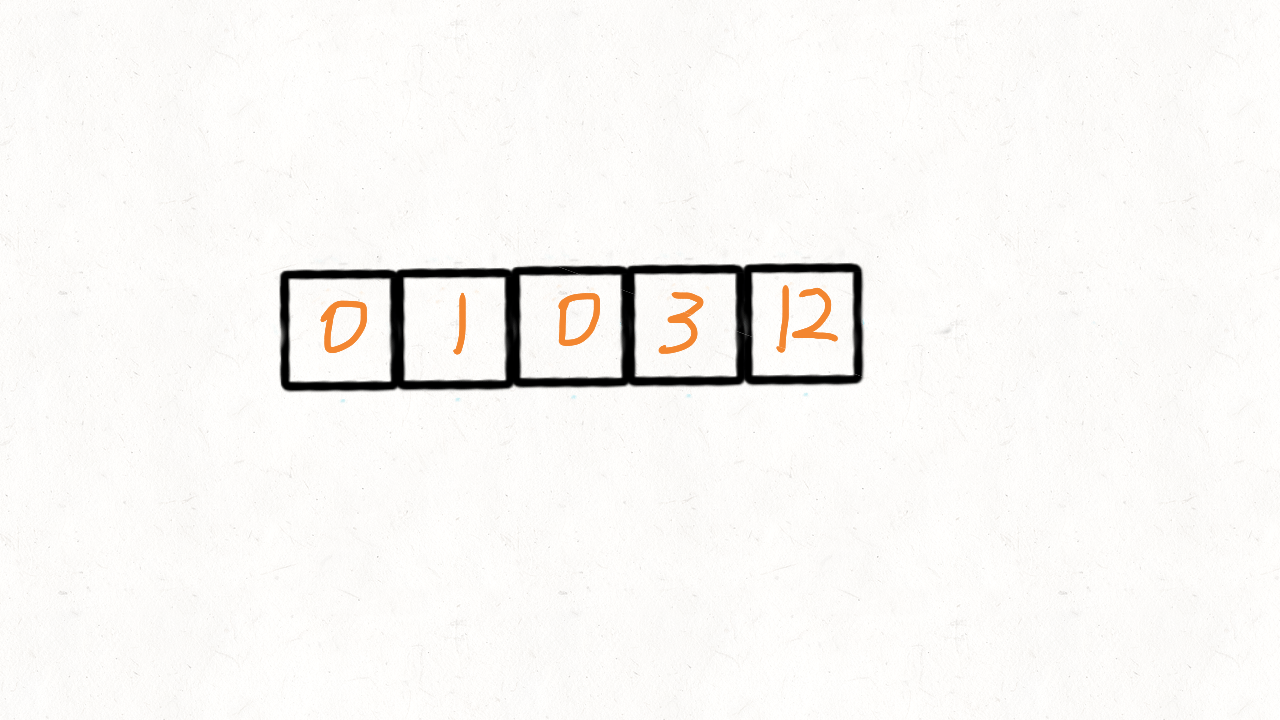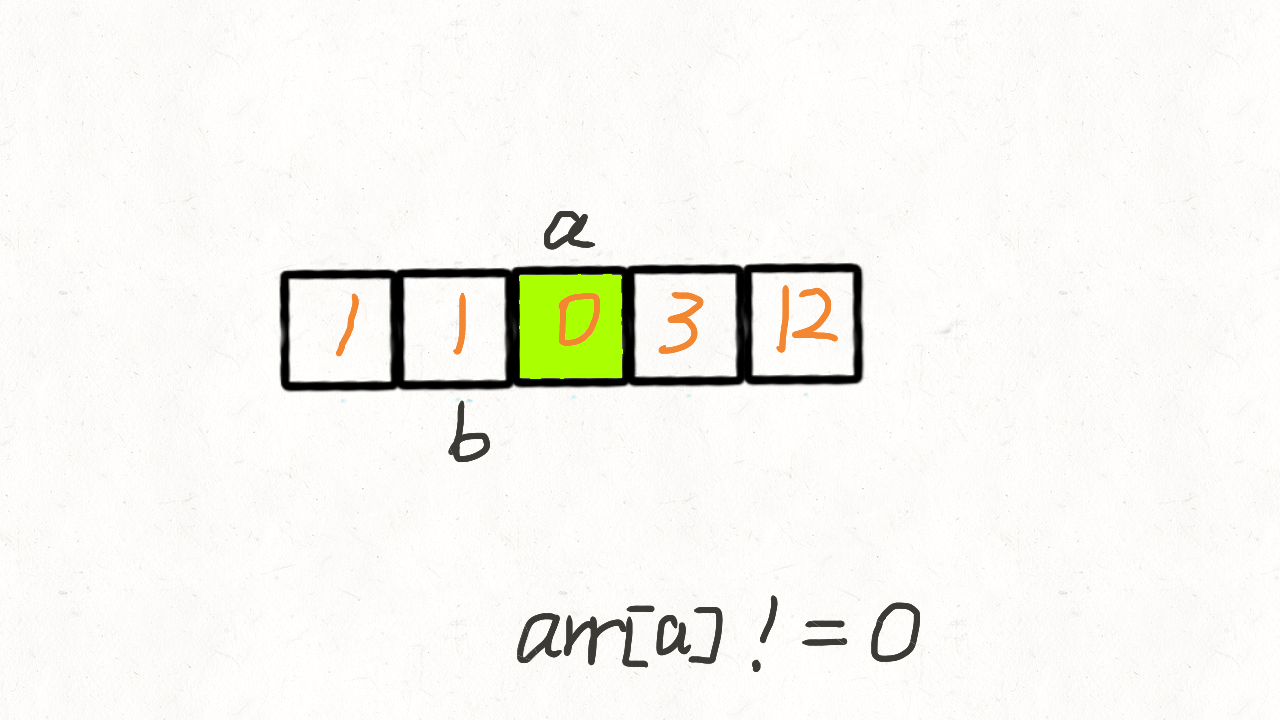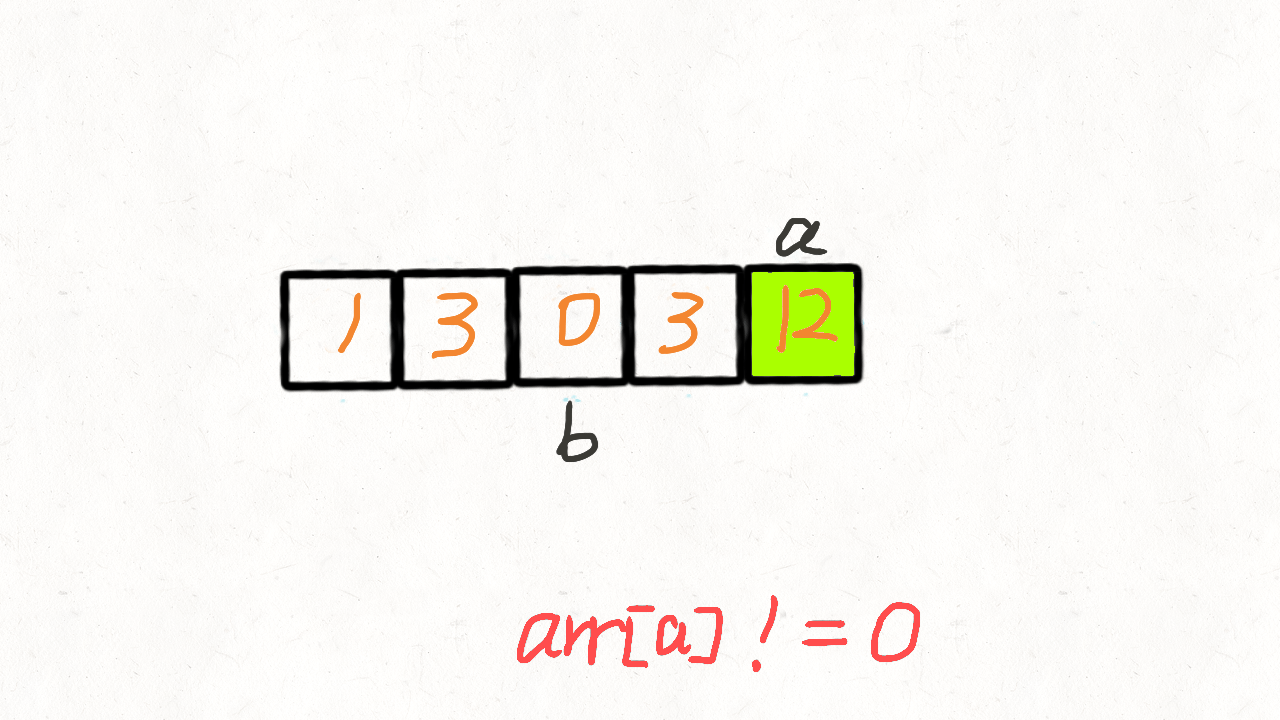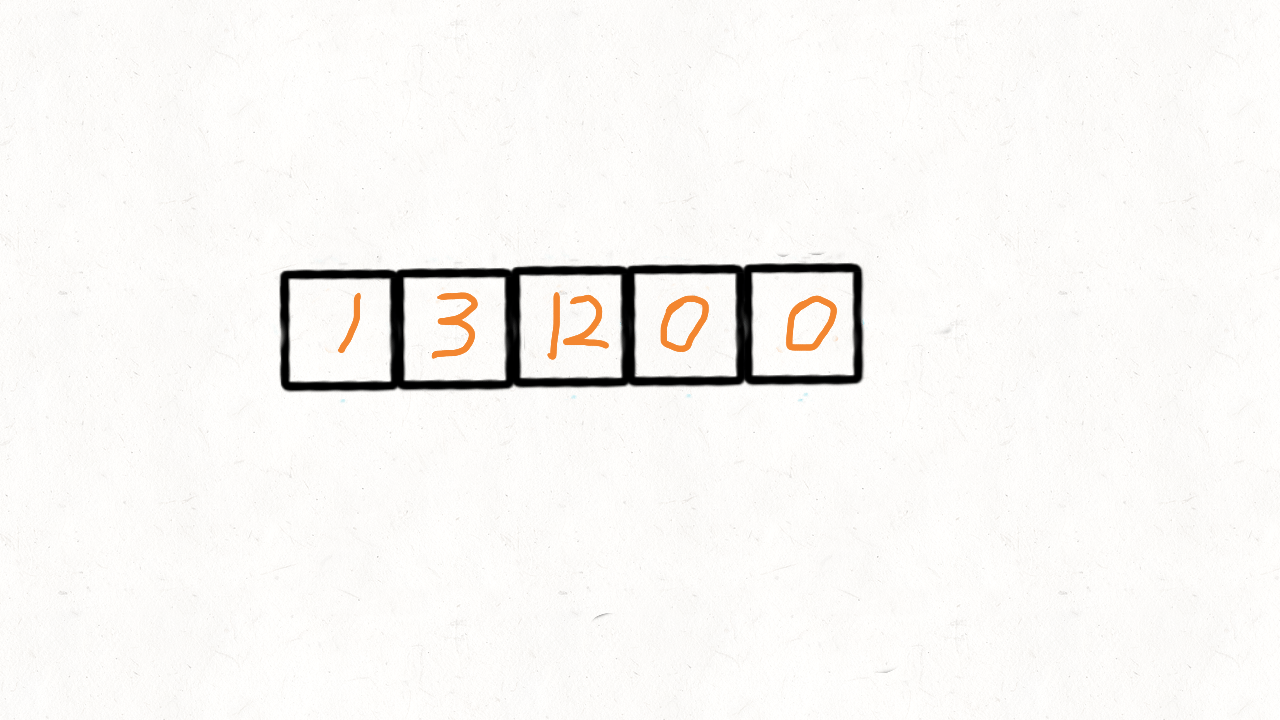
- 代码参考
1 class Solution { 2 public: 3 void swap(int &a,int &b) 4 { 5 int temp; 6 temp=a; 7 a=b; 8 b=temp; 9 } 10 void moveZeroes(vector<int>& nums) { 11 if(nums.empty()) 12 return; 13 int fast=0; 14 int slow=0; 15 for(fast=0;fast<nums.size();++fast) 16 { 17 if(nums[fast]!=0) 18 { 19 swap(nums[slow],nums[fast]); 20 ++slow; 21 } 22 } 23 } 24 };

- 题目分析
要在递增排序的数组中找到两个数,使得他们的和刚好为S,我们可以采用双指针法,一个指针begin指向数组头,一个指针end指向数组尾,
如果begin指针和end指针指向的两数之和cursum==sum,则直接将这两个数入栈;
如果cursum<sum,则++begin;
否则,--end;
题目还要求如果有多对数字的和等于S,则输出两个数的乘积最小的,按照我们上述的方法,就可以保证乘积最小,因为我们是从最小的地方开始的
- 代码参考
1 class Solution { 2 public: 3 vector<int> FindNumbersWithSum(vector<int> array,int sum) { 4 /* 5 两个指针,一个指针begin指向数组头,一个指针end指向数组尾 6 如果两个指针指向的元素之和等于S,直接返回 7 如果两个指针指向的元素之和小于s,++begin 8 如果两个指针指向的元素之和大于s,--end 9 */ 10 vector<int> B; 11 if(array.size()<2) 12 return B; 13 int begin=0; 14 int end=array.size()-1; 15 while(begin<=end) 16 { 17 int cursum=array[begin]+array[end]; 18 if(cursum==sum) 19 { 20 B.push_back(array[begin]); 21 B.push_back(array[end]); 22 break; 23 } 24 else if(cursum>sum) 25 --end; 26 else 27 ++begin; 28 } 29 return B; 30 } 31 };

- 问题分析
要找到和为S的连续正数序列,我们需要注意的是,其是连续的,因此我们也可以利用双指针来进行解答
两个指针,一个指针small指向1,另一个指针big指向small+1,
如果small和end之间的序列和cursum==sum,则直接将small和end之间的序列入栈。然后继续查找下一个序列
如果cursum>sum,则++small
否则,++big;
- 代码参考
1 class Solution { 2 public: 3 vector<vector<int> > FindContinuousSequence(int sum) { 4 //注意,我们要找的是连续的正整数序列 5 /* 6 两个指针,一个指针index1指向数组头,一个指针index2指向数组头+1 7 求两个指针之间的和cursum 8 如果cursum==sum,则直接将中间的所有序列全部压栈,然后继续搜索 9 如果cursum<sum,则++index2 10 否则,++index1 11 */ 12 vector<vector<int>> B; 13 int index1=1; 14 int index2=2; 15 while(index1<index2) 16 { 17 int cursum=(index1+index2)*(index2-index1+1)/2; 18 vector<int> onesum; 19 if(cursum==sum) 20 { 21 for(int i=index1;i<=index2;++i) 22 onesum.push_back(i); 23 B.push_back(onesum); 24 ++index2; 25 } 26 else if(cursum<sum) 27 ++index2; 28 else 29 ++index1; 30 } 31 return B; 32 } 33 };

- 问题分析
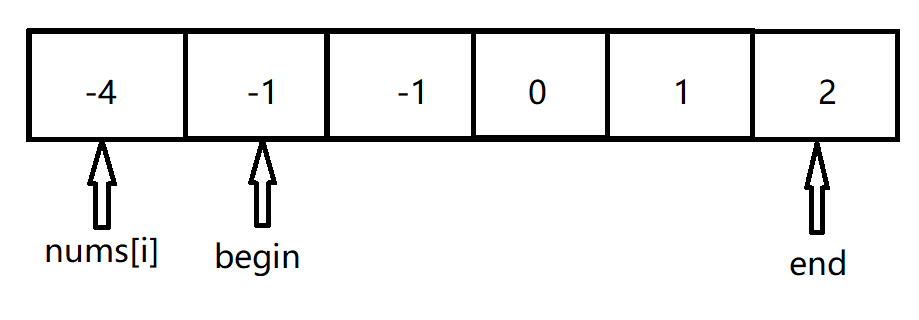
其实三数之和本质上可以转换为两数之和,从头到尾遍历整个数组,两个指针,begin指向nums[i+1],end指向数组尾,将问题转换为在begin和end之间找到和为-nums[i]的即可。在这个过程中,我们需要去除遍历重复的元素,
首先是在遍历nums[i]的时候,如果nums[i]和其前一个数相同,则应将此nums[i]跳过
在begin和end之间找到和为-nums[i]的两数之后,需要继续移动begin和end,
如果nums[begin]和其后一个数相同,则需要移动直到不同
如果nums[end]和其前一个数相同,也需要移动直到其不同
- 代码参考
1 class Solution { 2 public: 3 vector<vector<int>> threeSum(vector<int>& nums) { 4 vector<vector<int>> B; 5 if(nums.size()<3) 6 return B; 7 sort(nums.begin(),nums.end()); 8 int len=nums.size(); 9 for(int i=0;i<len;++i) 10 { 11 if(i>0&&nums[i]==nums[i-1]) 12 continue; 13 twoSum(B,nums,i+1,len-1,-nums[i],nums[i]); 14 } 15 return B; 16 } 17 void twoSum(vector<vector<int>> &B,vector<int> &nums,int begin,int end,int target,int value) 18 { 19 while(begin<end) 20 { 21 int sum=nums[begin]+nums[end]; 22 vector<int> onesum; 23 if(sum==target) 24 { 25 onesum.push_back(value); 26 onesum.push_back(nums[begin]); 27 onesum.push_back(nums[end]); 28 B.push_back(onesum); 29 while(begin<end&&nums[begin]==nums[begin+1]) 30 ++begin; 31 ++begin; 32 while(begin<end&&nums[end]==nums[end-1]) 33 --end; 34 --end; 35 } 36 else if(sum<target) 37 ++begin; 38 else 39 --end; 40 } 41 42 } 43 };

- 问题分析
这道题是类似于三数之和的,不同之处在于需要一直维护一个closedsum,如果当前|target-cursum|<|target-closedsum|,则需要更新closedsum
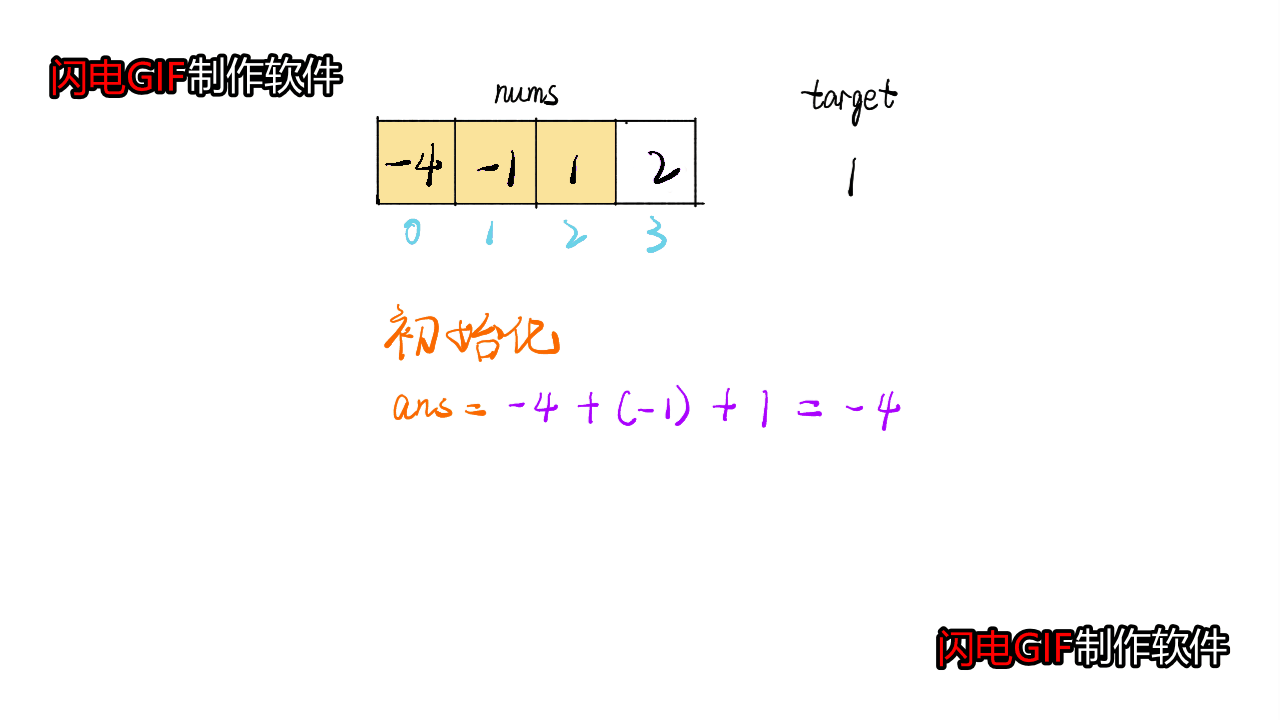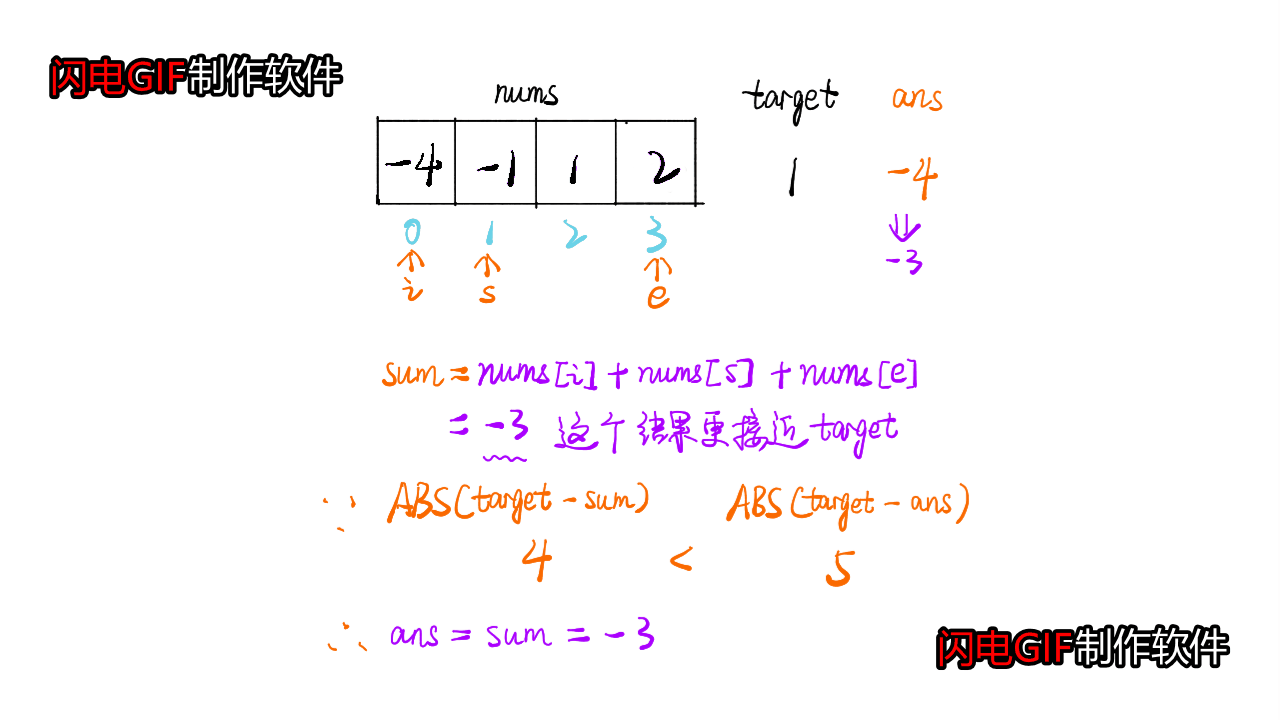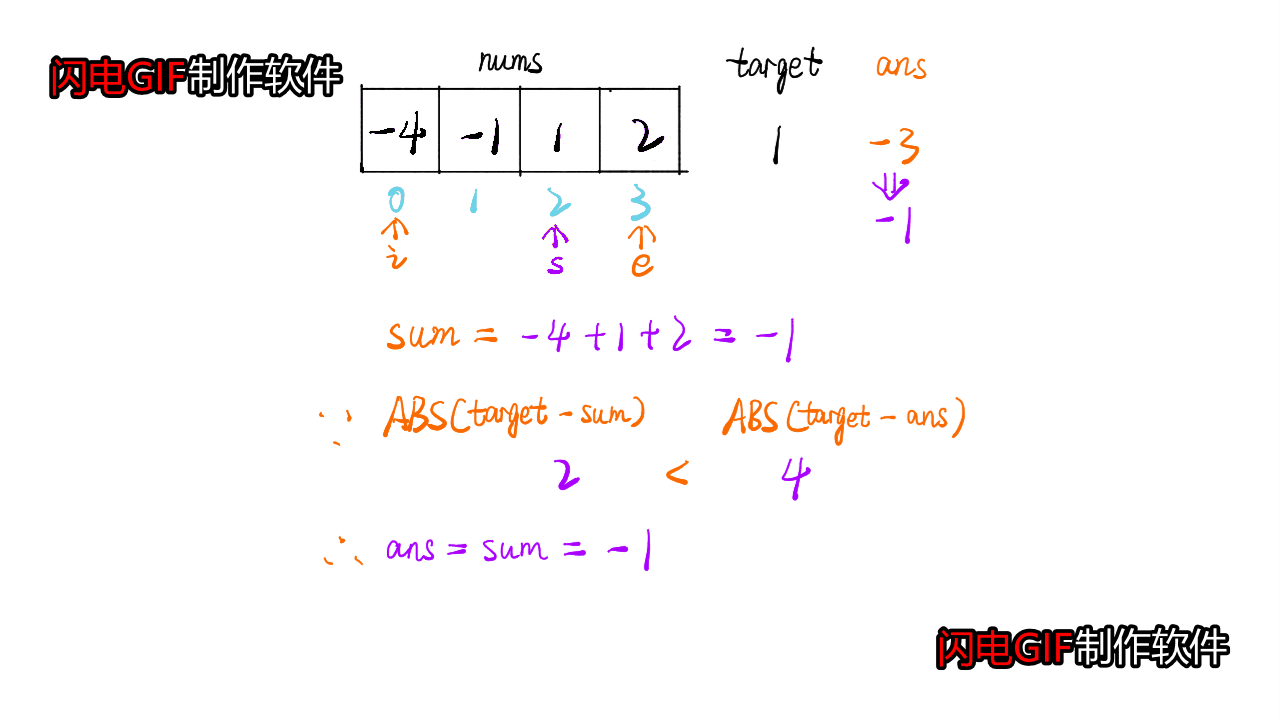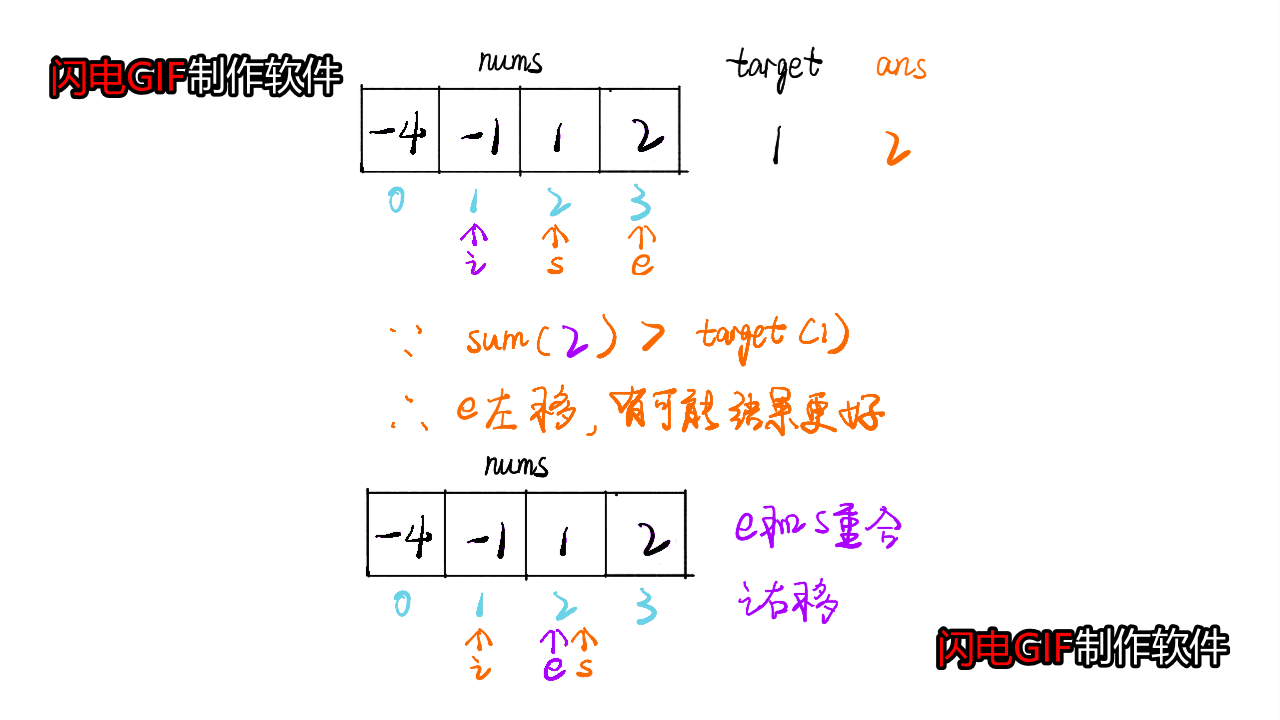
- 代码参考
1 class Solution { 2 public: 3 int threeSumClosest(vector<int>& nums, int target) { 4 if(nums.size()<3) 5 return 0; 6 int len=nums.size(); 7 sort(nums.begin(),nums.end()); 8 int closedsum=nums[0]+nums[1]+nums[2]; 9 for(int i=0;i<len;++i) 10 { 11 if(i>0&&nums[i]==nums[i-1]) 12 continue; 13 int begin=i+1; 14 int end=len-1; 15 while(begin<end) 16 { 17 int cursum=nums[i]+nums[begin]+nums[end]; 18 if(abs(target-cursum)<abs(target-closedsum)) 19 closedsum=cursum; 20 if(cursum<target) 21 ++begin; 22 else if(cursum>target) 23 --end; 24 else 25 { 26 closedsum=target; 27 break; 28 } 29 } 30 } 31 return closedsum; 32 } 33 };

- 题目分析
四数之和可以参照三数之和,使用四个指针(a<b<c<d),固定最小的a,b在最左边,我们可以知道,当固定a时,变成了三数之和,当固定a,b时,变成了两数之和,要实现没有重复的,则移动每个指针之前都需要思考怎么跳过重复的,如果cursum==target,则直接将四数存储在数组中,如果cursum<target,++begin,否则,--end
- 代码参考
1 class Solution { 2 public: 3 vector<vector<int>> fourSum(vector<int>& nums, int target) { 4 vector<vector<int>> B; 5 vector<int> onesum; 6 if(nums.size()<4) 7 return B; 8 int len=nums.size(); 9 sort(nums.begin(),nums.end()); 10 for(int i=0;i<len;++i) 11 { 12 if(i>0&&nums[i]==nums[i-1]) 13 continue; 14 for(int j=i+1;j<len;++j) 15 { 16 if(j>i+1&&nums[j]==nums[j-1]) 17 continue; 18 int begin=j+1; 19 int end=len-1; 20 while(begin<end) 21 { 22 int cursum=nums[i]+nums[j]+nums[begin]+nums[end]; 23 if(cursum==target) 24 { 25 onesum.push_back(nums[i]); 26 onesum.push_back(nums[j]); 27 onesum.push_back(nums[begin]); 28 onesum.push_back(nums[end]); 29 B.push_back(onesum); 30 onesum.clear(); 31 while(begin<end&&nums[begin]==nums[begin+1]) 32 ++begin; 33 ++begin; 34 while(begin<end&&nums[end]==nums[end-1]) 35 --end; 36 --end; 37 } 38 else if(cursum<target) 39 ++begin; 40 else 41 --end; 42 } 43 } 44 } 45 return B; 46 } 47 };

- 题目分析
首先分析合并两个链表的过程。我们的分析从合并两个链表的头结点开始。
若链表1的头结点的值小于链表2则将链表1的头结点作为合并后链表的头结点,反之也成立。
继续合并剩下的结点,由于两个链表中剩下的节点依然是排序的,因此合并这两个链表的步骤和前面的步骤是一样的。
- 代码参考
1 /* 2 struct ListNode { 3 int val; 4 struct ListNode *next; 5 ListNode(int x) : 6 val(x), next(NULL) { 7 } 8 };*/ 9 class Solution { 10 public: 11 //要实现合并排序的链表,只需要两个指针p1,p2分别指向两个链表的头,如果p1<p2,则将p1连接上去,否则,将p2连接上去 12 ListNode* Merge(ListNode* pHead1, ListNode* pHead2) 13 { 14 ListNode* head=nullptr; 15 if(pHead1==nullptr) 16 return pHead2; 17 else if(pHead2==nullptr) 18 return pHead1; 19 else 20 { 21 if(pHead1->val<pHead2->val) 22 { 23 head=pHead1; 24 head->next=Merge(pHead1->next, pHead2); 25 } 26 else 27 { 28 head=pHead2; 29 head->next=Merge(pHead1, pHead2->next); 30 } 31 } 32 return head; 33 } 34 };
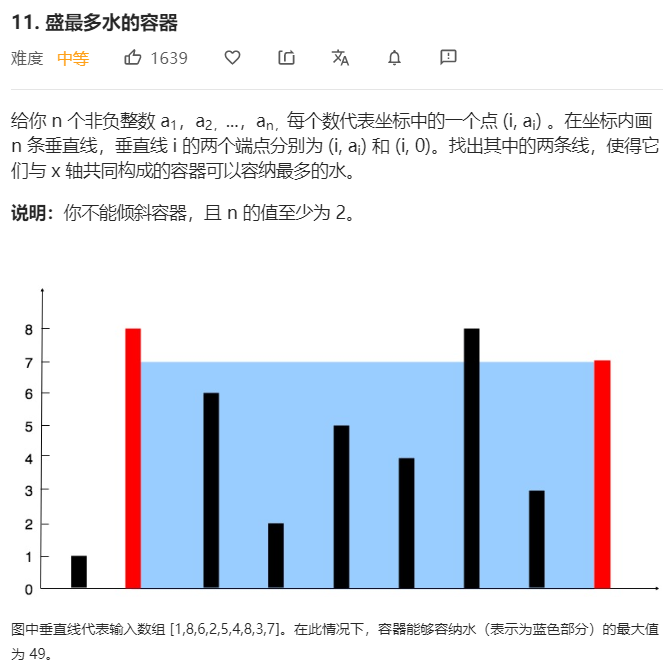
- 问题分析
首先要理解题意,题目中构成的容器的意思是,以两条垂线和X轴为界,是构成的一个U形的容器,刚开始我理解错了意思,以为是将其简单的加起来即可。
因此我们可以双指针法来进行实现,两个指针small,big分别指向数组头和数组尾,设置一个最大值,计算small和big构成容器的容积volumn,如果volumn<max,则将max更新,否则不更新。每次计算volumn后都将small和big指向的更小的那个指针进行移动。
为什么要移动最小的而不是最大的呢?由于我们是要找更大的,移动更小的只会让容积越来越小,下面我们以上述题目中的例子为例分析整个过程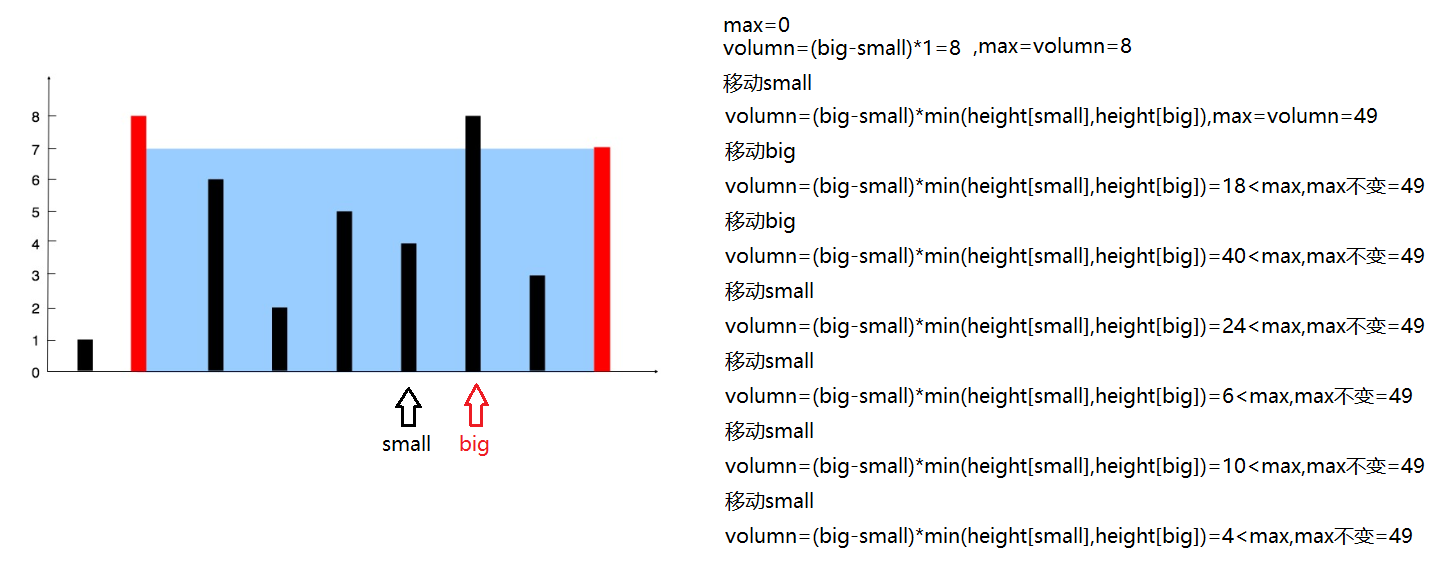
- 代码参考
1 class Solution { 2 public: 3 int maxArea(vector<int>& height) { 4 if(height.size()<2) 5 return 0; 6 int small=0; 7 int big=height.size()-1; 8 int max=0; 9 int volumn=0; 10 while(small<big) 11 { 12 volumn=(big-small)*min(height[small],height[big]); 13 if(volumn>max) 14 max=volumn; 15 if(height[small]<height[big]) 16 ++small; 17 else 18 --big; 19 } 20 return max; 21 } 22 };
- 题目描述

- 问题分析
首先我们需要判断链表是否有环的,如果链表是没有环的,则其是没有入口节点的
判断链表是否有环的方法:两个指针:快指针和慢指针,快指针每次移动两步,慢指针每次移动一步,如果两个相遇,则链表有环。否则,链表没有环。
确定链表有环之后,我们需要求出环的长度
求出环的长度之后,我们令两个指针都指向头结点,一个指针先移动环的长度这么多步,然后同时移动两个指针,相遇的地方就是环的入口节点处
- 代码参考
1 /* 2 struct ListNode { 3 int val; 4 struct ListNode *next; 5 ListNode(int x) : 6 val(x), next(NULL) { 7 } 8 }; 9 */ 10 class Solution { 11 public: 12 ListNode* EntryNodeOfLoop(ListNode* pHead) 13 { 14 //首先判断链表是否有环,要实现如此判断,我们可以使用双指针,一个快指针和一个慢指针, 15 //快指针每次走两步,慢指针每次走一步,如果相遇,则链表有环,否则链表没有环 16 if(pHead==nullptr||pHead->next==nullptr||pHead->next->next==nullptr) 17 return nullptr; 18 ListNode* fast=pHead->next->next; 19 ListNode* slow=pHead->next; 20 while(slow!=fast) 21 { 22 if(fast->next!=nullptr&&fast->next->next!=nullptr) 23 { 24 fast=fast->next->next; 25 slow=slow->next; 26 } 27 else 28 return nullptr; 29 } 30 //此时的链表是已经确认有环的了,因此我们需要求出环的长度 31 int len=1; 32 slow=slow->next; 33 while(slow!=fast) 34 { 35 ++len; 36 slow=slow->next; 37 } 38 //求出环的长度之后,我们令两个指针都指向链表的头结点,一个链表先走环的长度这么多步 39 slow=pHead; 40 fast=pHead; 41 for(int i=0;i<len;++i) 42 { 43 slow=slow->next; 44 } 45 while(slow!=fast) 46 { 47 slow=slow->next; 48 fast=fast->next; 49 } 50 return slow; 51 } 52 };
- 题目描述
要实现链表的旋转,由于链表的旋转是将链表后面的节点转换到前面来,并且有可能是k>len,即旋转的个数大于链表的长度的情况,因此思考需要将其转换成环形链表
实现环形链表的转换主要分为三步
第一步:将链表的尾结点指向链表的头结点,实现将链表转换为环形链表,并且求出链表的长度
第二步:找到新链表的头结点和尾结点,尾结点是(n-k%n-1),头结点是(n-k%n)
第三步:断开新链表的头结点和尾结点
- 代码参考
1 /** 2 * Definition for singly-linked list. 3 * struct ListNode { 4 * int val; 5 * ListNode *next; 6 * ListNode(int x) : val(x), next(NULL) {} 7 * }; 8 */ 9 class Solution { 10 public: 11 ListNode* rotateRight(ListNode* head, int k) { 12 /* 13 要分成三个步骤 14 第一步:将原始链表成环,原始链表的尾结点指向其头结点,使其成为一个闭环,并求出链表的长度 15 第二步:找到新链表的尾结点和头结点,尾结点为(n-k%n-1),头结点为(n-k%n) 16 第三步:断开新链表的头结点和尾结点 17 */ 18 if(head==nullptr) 19 return nullptr; 20 if(head->next==nullptr) 21 return head; 22 ListNode* old_tail=head; 23 //找到原始链表的尾结点并求长度 24 int len=1; 25 while(old_tail->next!=nullptr) 26 { 27 ++len; 28 old_tail=old_tail->next; 29 } 30 //将原始链表的尾结点指向其头结点 31 old_tail->next=head; 32 //找到新链表的尾结点 33 ListNode* new_tail=head; 34 for(int i=0;i<len-k%len-1;++i) 35 new_tail=new_tail->next; 36 ListNode* new_head=new_tail->next; 37 new_tail->next=nullptr; 38 return new_head; 39 } 40 };
- 题目描述
这道题本质上和之前做过的回文字符串是类似的,不同之处在于,对于单向链表,其尾结点没有指向前面的前驱结点,因此直接两个指针位于链表头和链表尾是不成立的。
因此,判断回文链表需要将链表的后半部分反转,才能实现和回文字符串类似的操作
具体步骤如下
第一步:找到链表的中间节点:利用快指针和慢指针,快指针每次走两步,慢指针每次走一步,当快指针到达尾结点时,慢指针到达终点
第二步:以慢指针为反转头结点对链表的后半部分进行反转
第三步:类似于回文字符串,依次进行判断

- 代码参考
1 /** 2 * Definition for singly-linked list. 3 * struct ListNode { 4 * int val; 5 * ListNode *next; 6 * ListNode(int x) : val(x), next(NULL) {} 7 * }; 8 */ 9 class Solution { 10 public: 11 bool isPalindrome(ListNode* head) { 12 //首先找到链表的中间节点 13 if(head==nullptr||head->next==nullptr) 14 return true; 15 //使用快节点和慢节点 16 ListNode* slow=head; 17 ListNode* fast=head; 18 while(fast&&fast->next) 19 { 20 slow=slow->next; 21 fast=fast->next->next; 22 } 23 //第二步,将slow后面的链表进行反转 24 ListNode* curNode=slow; 25 ListNode* nextNode=slow->next; 26 while(nextNode) 27 { 28 ListNode* next=nextNode->next; 29 nextNode->next=curNode; 30 curNode=nextNode; 31 nextNode=next; 32 } 33 slow->next=nullptr; 34 //第三步,判断是否对应项相等 35 while(head&&curNode) 36 { 37 if(head->val!=curNode->val) 38 return false; 39 head=head->next; 40 curNode=curNode->next; 41 } 42 return true; 43 44 } 45 };