目录
- 栈中存放任意类型的变量,但必须是auto修饰的,即自动类型的局部变量。随用随开,用完即消。
- 内存的分配和销毁是由系统自动完成的,不需要人工干预。
- 栈内存不可返回,调用函数就是开辟一个栈的空间,随用随开,用完即消。
- 栈的特点
栈的典型特点是先入后出,或者后入先出。只要是接口操作,分别是:判空、判满、压栈、出栈。
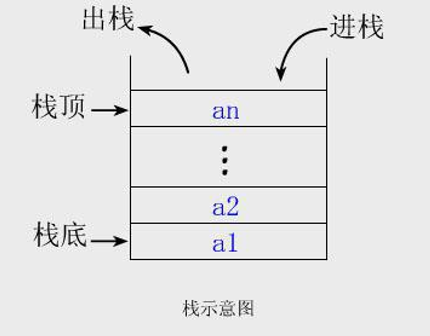
主要分为:栈的初始化、栈的判空、栈的判满、栈的压入和栈的弹出操作
栈的初始化:由于是线性结构,因此给栈初始化长度为我们所需要的长度
如果栈顶标号_top==0,则为空,如果栈顶标号_top==_len,则为满
栈的压入:由于栈顶标号_top指向待操作的元素,因此先插入元素,再将_top增加
栈的弹出:由于栈顶标号_top指向待插入的元素,因此要删除元素,需要先将_top减小,再实现元素的弹出
1 typedef struct _stack 2 { 3 int _len; 4 char* _space; 5 int _top; 6 }Stack; 7 8 void initStack(Stack* s, int len) 9 { 10 s->_top = 0; 11 s->_space = new char[sizeof(char)*len];//s->_space=(char*)malloc(sizeof(char)*len) 12 s->_len = len; 13 } 14 15 bool isStackFull(Stack* s) 16 { 17 return s->_top == s->_len; 18 } 19 20 bool isStackEmpty(Stack* s) 21 { 22 return s->_top == 0; 23 } 24 25 void mypush(Stack* s, int ch) 26 { 27 s->_space[s->_top++] = ch; 28 } 29 30 char mypop(Stack* s) 31 { 32 return s->_space[--s->_top]; 33 }
使用C++类封装后栈的线性存储
mystack.h
1 #pragma once 2 class mystack 3 { 4 public: 5 //栈的初始化 6 void initStack(int len); 7 //栈的判空 8 bool isEmpty(); 9 //栈的判满 10 bool isFull(); 11 //栈的压入 12 void mypush(char ch); 13 //栈的弹出 14 char mypop(); 15 16 private: 17 int _len; 18 char* _space; 19 int _top; 20 };
mystack.cpp
1 #include "mystack.h" 2 3 //栈的初始化 4 void mystack::initStack(int len) 5 { 6 _len = len; 7 _space = new char[len]; 8 _top = 0; 9 } 10 11 //栈的判空 12 bool mystack::isEmpty() 13 { 14 return _top == 0; 15 } 16 17 //栈的判满 18 bool mystack::isFull() { 19 return _top == _len; 20 } 21 22 //栈的压入 23 void mystack::mypush(char ch) { 24 _space[_top++] = ch; 25 } 26 27 //栈的弹出 28 char mystack::mypop() 29 { 30 return _space[--_top]; 31 }
main
1 #include <iostream> 2 #include "mystack.h" 3 4 using namespace std; 5 6 int main() 7 { 8 mystack s; 9 s.initStack(100); 10 for (int ch = 'a'; ch <= 'z'; ++ch) 11 { 12 s.mypush(ch); 13 } 14 while (!s.isEmpty()) 15 { 16 cout << s.mypop() << " "; 17 } 18 cout << endl; 19 }
栈的链式存储即栈中每个元素是用链表来实现的,因此设计时选择表头作为栈顶指针,而不是表尾,不同于线式存储,由于是链表,因此其没有判满操作
注意:栈的链式存储中,_top是位于链表尾部的,由于要满足先入先出原则,使用头插法可以实现,因此申请一个_top为头结点
由于其是链式存储的,因此是利用链表来实现栈的,链表必然涉及到其头结点,因此要初始化即需要申请一个链表节点_top,_top.next=nullptr
链式存储是不需要判满的
链表的判空:当_top的下一个节点为空,其则为空
链表的压入操作:将节点利用头插法插入链表,让新来的节点有所指向
链表的删除操作:删除_top的下一个结点
1 typedef struct _node 2 { 3 char data; 4 struct _node* next; 5 }Node; 6 7 typedef struct _stacklist 8 { 9 Node* _top; 10 }Stacklist; 11 12 void initStacklist(Stacklist* s) 13 { 14 s->_top = nullptr; 15 } 16 17 bool isStacklistEmpty(Stacklist* s) 18 { 19 return s->_top == nullptr; 20 } 21 22 //使用尾插法来实现 23 void stacklistpush(Stacklist* s, char ch) 24 { 25 Node* cur = new Node; 26 cur->data = ch; 27 cur->next = s->_top; 28 s->_top = cur; 29 } 30 31 char stacklistpop(Stacklist* s) 32 { 33 Node* t = s->_top; 34 char ch = t->data; 35 s->_top = s->_top->next; 36 return ch; 37 delete t; 38 }
使用C++封装后的栈的链式存储
mystackList.h
1 #pragma once 2 //栈的链式存储 3 typedef struct _node { 4 char data; 5 struct _node* next; 6 }Node; 7 class mystackList 8 { 9 public: 10 //链式存储就不需要判满了 11 void initStackList(); 12 bool isStackEmpty(); 13 void mypush(char ch); 14 char mypop(); 15 private: 16 Node* _top; 17 };
mystackList.cpp
1 #include "mystackList.h" 2 3 //栈的初始化 4 void mystackList::initStackList() 5 { 6 _top = new Node; 7 _top->next = nullptr; 8 } 9 10 //判断栈是否为空 11 bool mystackList::isStackEmpty() { 12 return _top->next == nullptr; 13 } 14 15 //入栈,使用尾插法实现 16 void mystackList::mypush(char ch) 17 { 18 Node* cur = new Node; 19 cur->data = ch; 20 cur->next = _top->next; 21 _top->next = cur; 22 } 23 //出栈,相当于链表的出栈 24 char mystackList::mypop() 25 { 26 Node* t = _top->next; 27 char ch = t->data; 28 _top = _top->next; 29 return ch; 30 delete t; 31 }
main.cpp
1 #include <iostream> 2 #include "mystack.h" 3 #include "mystackList.h" 4 5 using namespace std; 6 7 int main() 8 { 9 /*mystack s; 10 s.initStack(100); 11 for (int ch = 'a'; ch <= 'z'; ++ch) 12 { 13 s.mypush(ch); 14 } 15 while (!s.isEmpty()) 16 { 17 cout << s.mypop() << " "; 18 } 19 cout << endl;*/ 20 mystackList s; 21 s.initStackList(); 22 for (char ch = 'a'; ch <= 'z'; ++ch) 23 { 24 s.mypush(ch); 25 } 26 while (!s.isStackEmpty()) 27 cout << s.mypop() << " "; 28 cout << endl; 29 }
- 题目描述:打印地图版:从地图的某一点开始,打印出其所能走通的路径
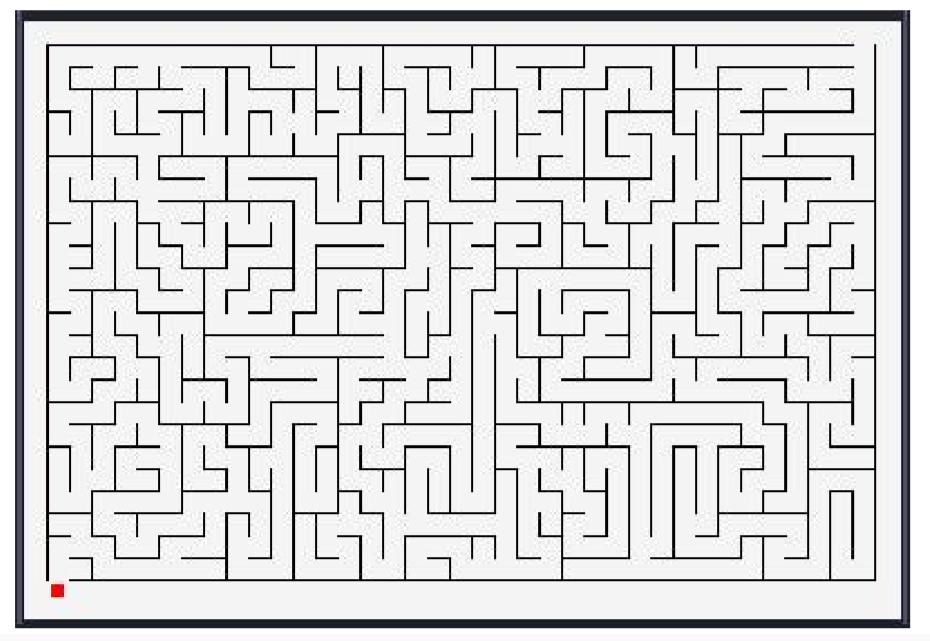
- 代码参考
mystack.h
1 typedef struct _point 2 { 3 int _x; 4 int _y; 5 }Point; 6 7 typedef struct _node 8 { 9 Point data; 10 struct _node* next; 11 }Node; 12 13 typedef struct _stacklist 14 { 15 Node* _top; 16 }StackList;
mystack.cpp
1 #include <iostream> 2 #include "mystack.h" 3 using namespace std; 4 5 6 void initStacklist(StackList* s) 7 { 8 s->_top = nullptr; 9 } 10 11 bool isStacklistEmpty(StackList* s) 12 { 13 return s->_top == nullptr; 14 } 15 16 void mypush(StackList* s, Point data) 17 { 18 Node* cur = new Node; 19 cur->data = data; 20 cur->next = s->_top; 21 s->_top = cur; 22 } 23 24 Point mypop(StackList* s) 25 { 26 Node* t = s->_top; 27 Point data = t->data; 28 s->_top = s->_top->next; 29 return data; 30 delete t; 31 }
main.cpp
#include <iostream> #include "mystack.h" using namespace std; #define MAXROW 10 #define MAXLINE 10 int maze[MAXROW][MAXLINE] = { 1,1,1,1,1,1,1,1,1,1, 0,0,0,1,1,1,1,1,1,1, 1,1,0,1,1,1,1,1,1,1, 1,1,0,0,0,0,1,1,1,1, 1,1,0,1,1,0,1,1,1,1, 1,1,0,1,1,0,1,1,1,1, 1,1,1,1,1,0,1,1,1,1, 1,1,1,1,1,0,0,0,1,1, 1,1,1,1,1,1,1,0,0,0, 1,1,1,1,1,1,1,1,1,1, }; void displyMaze() { for (int i = 0; i < MAXROW; i++) { for (int j = 0; j < MAXLINE; j++) { if (maze[i][j] == 1) printf("%2s", " *"); else if (maze[i][j] == 2) printf("%2s", " #"); else printf("%2s", " "); } putchar(10); } printf(" ==================== "); } StackList s; void visit(int x, int y) { Point p = { x,y }; mypush(&s, p); } int main() { Point sp = { 1,0 }; Point ep = { 8,9 }; displyMaze(); mypush(&s, sp); int flag = 0; while (!isStacklistEmpty(&s)) { Point t = mypop(&s); maze[t._x][t._y] = 2;//走过的路径设置为2 system("cls"); displyMaze(); if (t._y - 1 >= 0 && maze[t._x][t._y - 1] == 0) visit(t._x, t._y - 1); if (t._y + 1 <= 9 && maze[t._x][t._y + 1] == 0) visit(t._x, t._y + 1); if (t._x - 1 >= 0 && maze[t._x - 1][t._y] == 0) visit(t._x - 1, t._y); if (t._x + 1 >= 0 && maze[t._x + 1][t._y] == 0) visit(t._x + 1, t._y); if (t._x == ep._x && t._y == ep._y) { flag = 1; } if (flag == 1) cout << "find the path" << endl; else cout << "find no path"; } return 0; }
- 题目分析
首先区分栈和队列,队列是先入先出,栈是先入后出
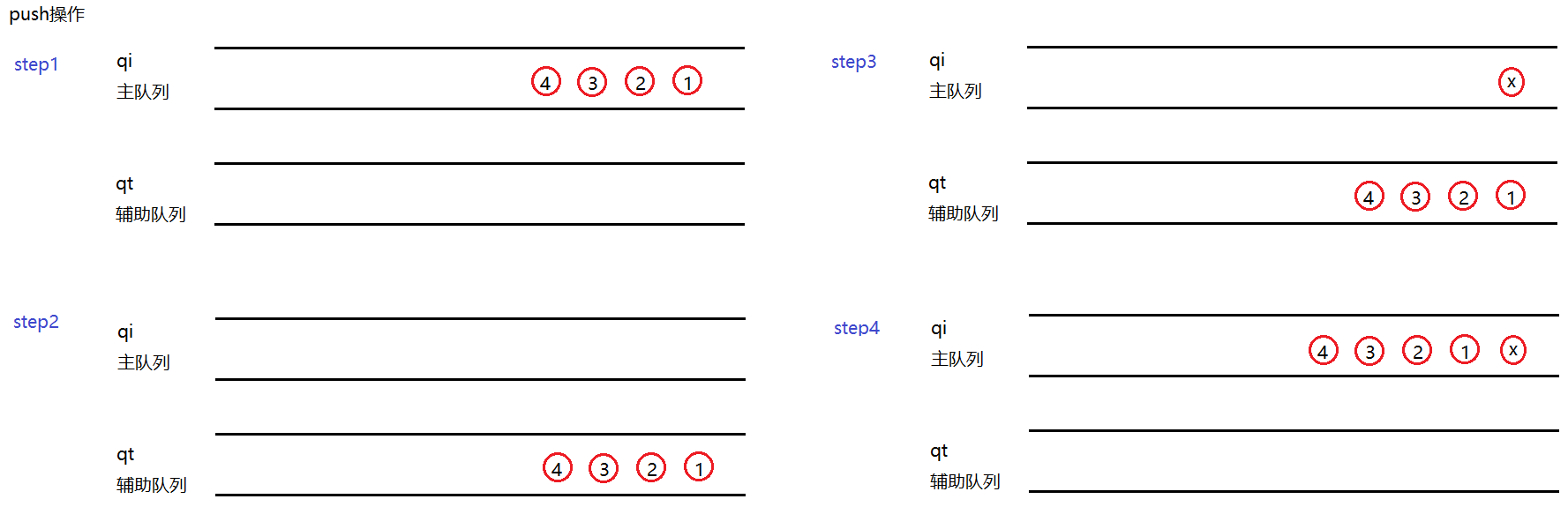
由于队列是先入先出,栈是先入后出,因此要利用队列实现栈,则需要借助辅助队列即可
对于压栈操作,如果主队列中有元素,可以将主队列qi中的元素以队列的方式放入辅助队列qt,将元素x插入主队列后再将辅助队列中的元素插入到主队列中,这样即可实现先入先出操作
对于JAVA中的栈常见操作
栈的实例化 Stack stack=new Stack(); 泛化性实例化 Stack<Integer> s=new Stack<Integer>(); s.empty() 判读栈是否为空 s.peek() 取栈顶值,不出栈 s.push() 入栈 s.pop() 出栈
对于JAVA中的队列常见的操作
队列的申请: Queue<Integer> queue=new LinkedList<Integer>(); add 增加一个元素,如果队列已满,则抛出异常 remove 溢出并返回队列头部的元素,如果队列为空,则抛出异常 element 返回队列头部的元素,如果队列为空,则抛出异常 offer 添加一个元素并返回true,如果队列已满,则返回false poll 返回并移除队列头部的元素,如果队列为空,则返回null peek 返回队列头部的元素,如果队列为空,则返回null put 添加一个元素,若队列满,则阻塞 take 移除并返回队列头部的元素,如果队列为空,则阻塞。
- 代码参考
1 class MyStack { 2 public: 3 /** Initialize your data structure here. */ 4 //借助辅助队列将要插入的元素排至队列头 5 queue<int> qi; 6 queue<int> qt; 7 MyStack() { 8 9 } 10 11 /** Push element x onto stack. */ 12 void push(int x) { 13 while(!qi.empty()) 14 { 15 qt.push(qi.front()); 16 qi.pop(); 17 } 18 qi.push(x); 19 while(!qt.empty()) 20 { 21 qi.push(qt.front()); 22 qt.pop(); 23 } 24 25 } 26 27 /** Removes the element on top of the stack and returns that element. */ 28 int pop() { 29 int temp=qi.front(); 30 qi.pop(); 31 return temp; 32 } 33 34 /** Get the top element. */ 35 int top() { 36 return qi.front(); 37 } 38 39 /** Returns whether the stack is empty. */ 40 bool empty() { 41 return qi.empty(); 42 } 43 }; 44 45 /** 46 * Your MyStack object will be instantiated and called as such: 47 * MyStack* obj = new MyStack(); 48 * obj->push(x); 49 * int param_2 = obj->pop(); 50 * int param_3 = obj->top(); 51 * bool param_4 = obj->empty(); 52 */
- JAVA代码参考
1 class MyStack { 2 3 Queue<Integer> qi; 4 Queue<Integer> qt; 5 /** Initialize your data structure here. */ 6 public MyStack() { 7 qi=new LinkedList<Integer>(); 8 qt=new LinkedList<Integer>(); 9 } 10 11 12 /** Push element x onto stack. */ 13 public void push(int x) { 14 while(!qi.isEmpty()) 15 { 16 qt.offer(qi.poll()); 17 } 18 qi.offer(x); 19 while(!qt.isEmpty()) 20 { 21 qi.offer(qt.poll()); 22 } 23 } 24 25 /** Removes the element on top of the stack and returns that element. */ 26 public int pop() { 27 return qi.poll(); 28 } 29 30 /** Get the top element. */ 31 public int top() { 32 return qi.peek(); 33 } 34 35 /** Returns whether the stack is empty. */ 36 public boolean empty() { 37 return qi.isEmpty(); 38 } 39 } 40 41 /** 42 * Your MyStack object will be instantiated and called as such: 43 * MyStack obj = new MyStack(); 44 * obj.push(x); 45 * int param_2 = obj.pop(); 46 * int param_3 = obj.top(); 47 * boolean param_4 = obj.empty(); 48 */

- 问题分析
使用两个栈来实现一个队列,即由先入后出改成先入先出,一个栈作为辅助栈,一个栈作为主栈 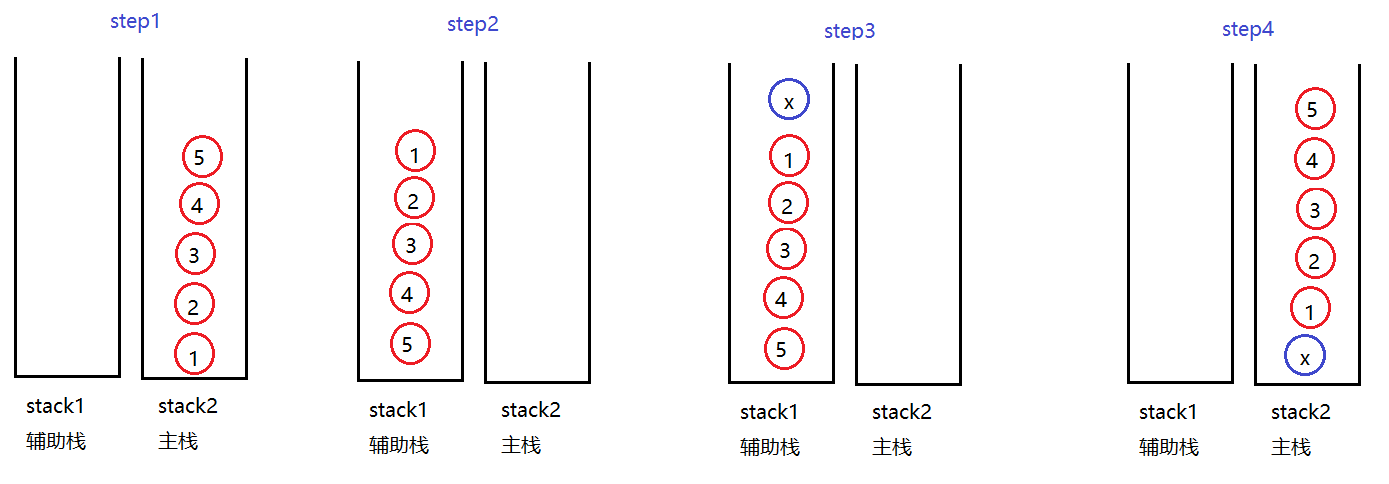
- 代码参考
1 class Solution 2 { 3 public: 4 void push(int node) { 5 while(!stack2.empty()) 6 { 7 stack1.push(stack2.top()); 8 stack2.pop(); 9 } 10 stack1.push(node); 11 while(!stack1.empty()) 12 { 13 stack2.push(stack1.top()); 14 stack1.pop(); 15 } 16 } 17 18 int pop() { 19 if(stack2.empty()) 20 return 0; 21 int temp=stack2.top(); 22 stack2.pop(); 23 return temp; 24 } 25 26 private: 27 stack<int> stack1;//主栈 28 stack<int> stack2;//辅助栈 29 };
- JAVA参考代码
1 class MyQueue { 2 3 /* 4 栈是先进后出 5 队列是先进先出 6 要用栈实现队列,可以利用辅助栈,两个栈,一个主栈,一个辅助栈 7 如果主栈有元素,插入元素时,先将主栈入辅助栈,将新的元素插入主栈后再将辅助栈的元素入主栈 8 */ 9 //首先申请两个栈,一个主栈一个辅助栈 10 Stack<Integer> si; 11 Stack<Integer> st; 12 /** Initialize your data structure here. */ 13 public MyQueue() { 14 si=new Stack<Integer>(); 15 st=new Stack<Integer>(); 16 } 17 18 /** Push element x to the back of queue. */ 19 public void push(int x) { 20 //如果主栈中有元素,则将主栈中所有元素入辅助栈 21 while(!si.isEmpty()) 22 { 23 st.push(si.peek()); 24 si.pop(); 25 } 26 //然后将待插入元素入主栈 27 si.push(x); 28 //然后将辅助栈中元素入主栈 29 while(!st.isEmpty()) 30 { 31 si.push(st.peek()); 32 st.pop(); 33 } 34 } 35 36 /** Removes the element from in front of queue and returns that element. */ 37 public int pop() { 38 int temp=si.peek(); 39 si.pop(); 40 return temp; 41 } 42 43 /** Get the front element. */ 44 public int peek() { 45 return si.peek(); 46 } 47 48 /** Returns whether the queue is empty. */ 49 public boolean empty() { 50 return si.isEmpty(); 51 } 52 } 53 54 /** 55 * Your MyQueue object will be instantiated and called as such: 56 * MyQueue obj = new MyQueue(); 57 * obj.push(x); 58 * int param_2 = obj.pop(); 59 * int param_3 = obj.peek(); 60 * boolean param_4 = obj.empty(); 61 */

- 问题分析
要实现包含min函数的栈,即实现一个最小栈,最小栈的栈顶就是当前元素中的最小值
使用两个栈来实现:数据栈和最小栈,数据栈每次正常压入数据,最小栈每次压入最小数据,设待插入元素为x,如最小栈为空或者x小于栈顶元素,则将x插入最小栈,否则将栈顶元素插入到最小栈中
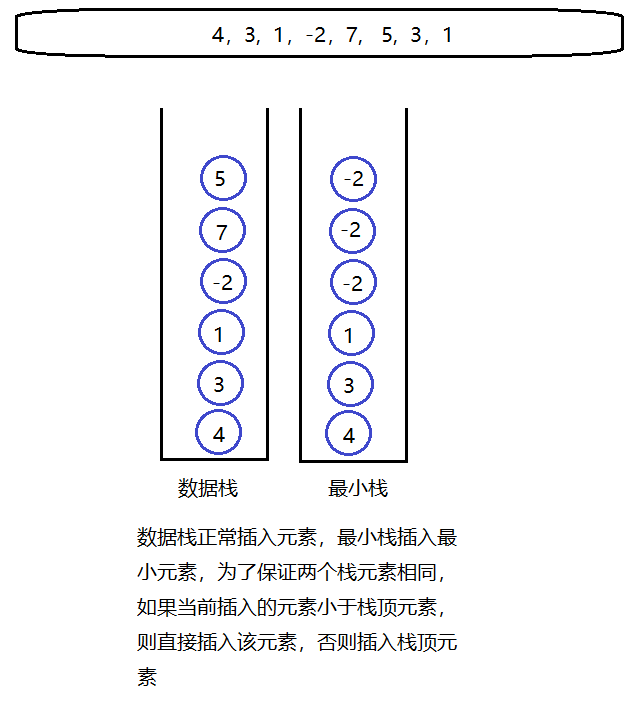
- 代码参考
1 class MinStack { 2 public: 3 /** initialize your data structure here. */ 4 MinStack() { 5 6 } 7 stack<int> data; 8 stack<int> mmin; 9 10 void push(int x) { 11 //数据栈正常压入数据 12 data.push(x); 13 if(mmin.empty()||x<mmin.top()) 14 { 15 mmin.push(x); 16 } 17 else 18 mmin.push(mmin.top()); 19 } 20 21 void pop() { 22 if(!data.empty()&&!mmin.empty()) 23 { 24 data.pop(); 25 mmin.pop(); 26 } 27 } 28 29 int top() { 30 return data.top(); 31 } 32 33 int min() { 34 return mmin.top(); 35 } 36 }; 37 38 /** 39 * Your MinStack object will be instantiated and called as such: 40 * MinStack* obj = new MinStack(); 41 * obj->push(x); 42 * obj->pop(); 43 * int param_3 = obj->top(); 44 * int param_4 = obj->min(); 45 */
- JAVA代码参考
1 class MinStack { 2 3 //要实现包含Min函数的栈,需要用两个栈来实现,一个栈正常插入删除数据,一个栈存入当前最小元素 4 /* 5 主栈正常插入数据,对于最小栈 6 当栈为空,则主栈和最小栈均插入待插入元素 7 当栈非空且待插入元素小于栈顶元素,则主栈和最小栈均插入待插入元素 8 当栈非空且待插入元素大于栈顶元素,则主栈正常插入元素,最小栈插入栈顶元素 9 */ 10 /** initialize your data structure here. */ 11 Stack<Integer> mystack; 12 Stack<Integer> MinStack; 13 public MinStack() { 14 mystack=new Stack<Integer>(); 15 MinStack=new Stack<Integer>(); 16 } 17 18 public void push(int x) { 19 //主栈正常插入数据 20 mystack.push(x); 21 //若当前栈不为空且待插入元素小于栈顶元素,则直接将栈顶元素插入 22 if(!MinStack.empty()&&x>MinStack.peek()) 23 MinStack.push(MinStack.peek()); 24 else 25 MinStack.push(x); 26 } 27 28 public void pop() { 29 MinStack.pop(); 30 mystack.pop(); 31 } 32 33 public int top() { 34 return mystack.peek(); 35 } 36 37 public int min() { 38 return MinStack.peek(); 39 } 40 } 41 42 /** 43 * Your MinStack object will be instantiated and called as such: 44 * MinStack obj = new MinStack(); 45 * obj.push(x); 46 * obj.pop(); 47 * int param_3 = obj.top(); 48 * int param_4 = obj.min(); 49 */
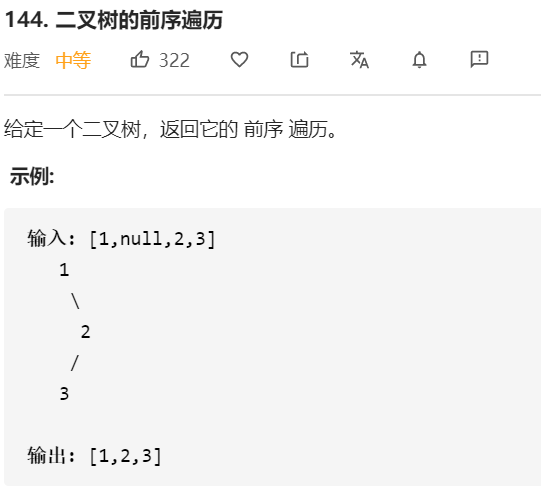
- 问题分析
二叉树的前序遍历序列,即先访问根节点,再访问左子树节点,再访问右子树节点
要实现二叉树的前序遍历序列,即借助辅助栈,从根节点开始,每次迭代弹出当前栈顶元素,将其孩子节点压入栈中,先压右子树节点,再压入左子树节点
在二叉树的先序遍历中,每个节点会被访问两次,第一次是入栈,此时就输出,第二次是出栈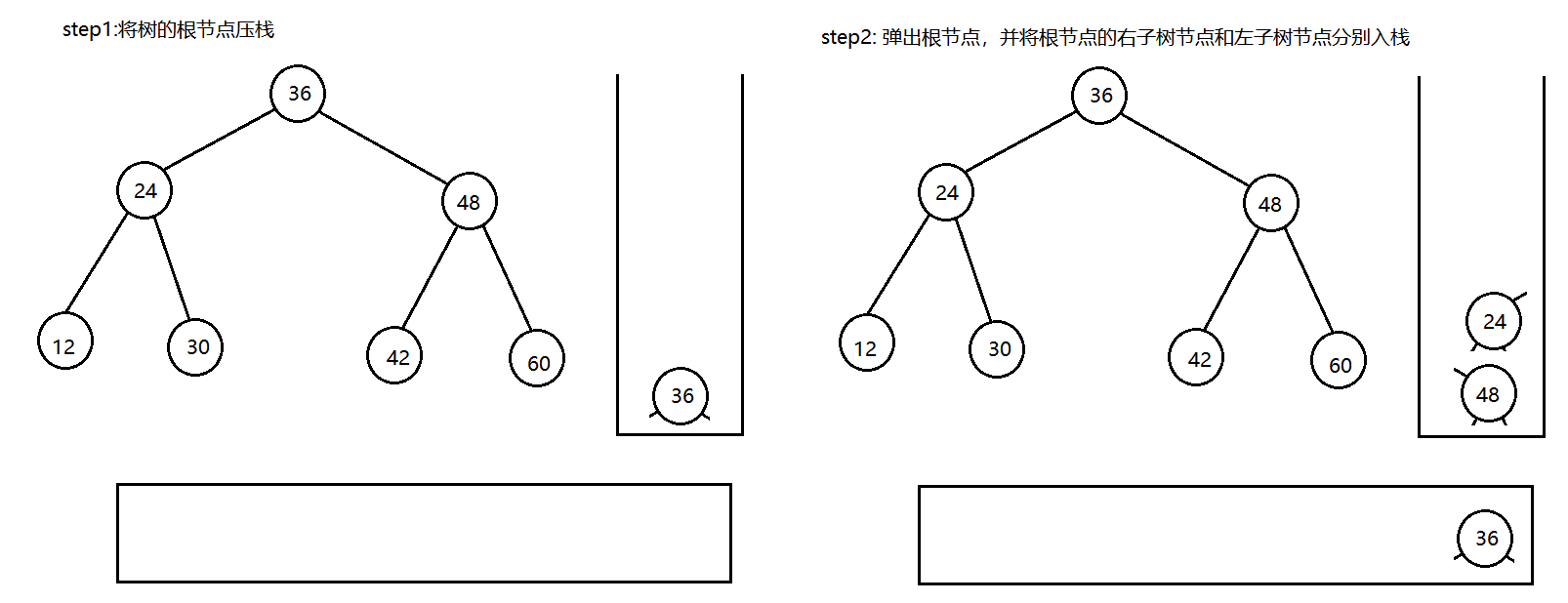
- 代码参考
1 /** 2 * Definition for a binary tree node. 3 * struct TreeNode { 4 * int val; 5 * TreeNode *left; 6 * TreeNode *right; 7 * TreeNode(int x) : val(x), left(NULL), right(NULL) {} 8 * }; 9 */ 10 class Solution { 11 public: 12 vector<int> preorderTraversal(TreeNode* root) { 13 vector<int> B; 14 if(root==nullptr) 15 return B; 16 stack<TreeNode*> s; 17 s.push(root); 18 while(!s.empty()) 19 { 20 TreeNode* t=s.top(); 21 B.push_back(t->val); 22 s.pop(); 23 if(t->right) 24 s.push(t->right); 25 if(t->left) 26 s.push(t->left); 27 } 28 return B; 29 } 30 };
- JAVA代码参考
1 /** 2 * Definition for a binary tree node. 3 * public class TreeNode { 4 * int val; 5 * TreeNode left; 6 * TreeNode right; 7 * TreeNode() {} 8 * TreeNode(int val) { this.val = val; } 9 * TreeNode(int val, TreeNode left, TreeNode right) { 10 * this.val = val; 11 * this.left = left; 12 * this.right = right; 13 * } 14 * } 15 */ 16 class Solution { 17 public List<Integer> preorderTraversal(TreeNode root) { 18 /* 19 二叉树的前序遍历:先访问根节点,再访问左子树节点,再访问右子树节点 20 要实现二叉树的前序遍历,可以借助辅助栈,每次迭代弹出当前栈顶元素,然后将其孩子节点入栈,先压入右子树节点,再压入左子树节点 21 */ 22 List<Integer> list=new ArrayList<Integer>(); 23 if(root==null) 24 return list; 25 Stack<TreeNode> s=new Stack<TreeNode>(); 26 //首先将根节点压入 27 s.push(root); 28 while(!s.empty()) 29 { 30 //首先将栈顶元素压入 31 root=s.peek(); 32 list.add(root.val); 33 //然后将栈顶元素弹出 34 s.pop(); 35 //首先将右子树节点压入 36 if(root.right!=null) 37 s.push(root.right); 38 //然后将左子树节点压入 39 if(root.left!=null) 40 s.push(root.left); 41 } 42 return list; 43 } 44 }
- 问题分析
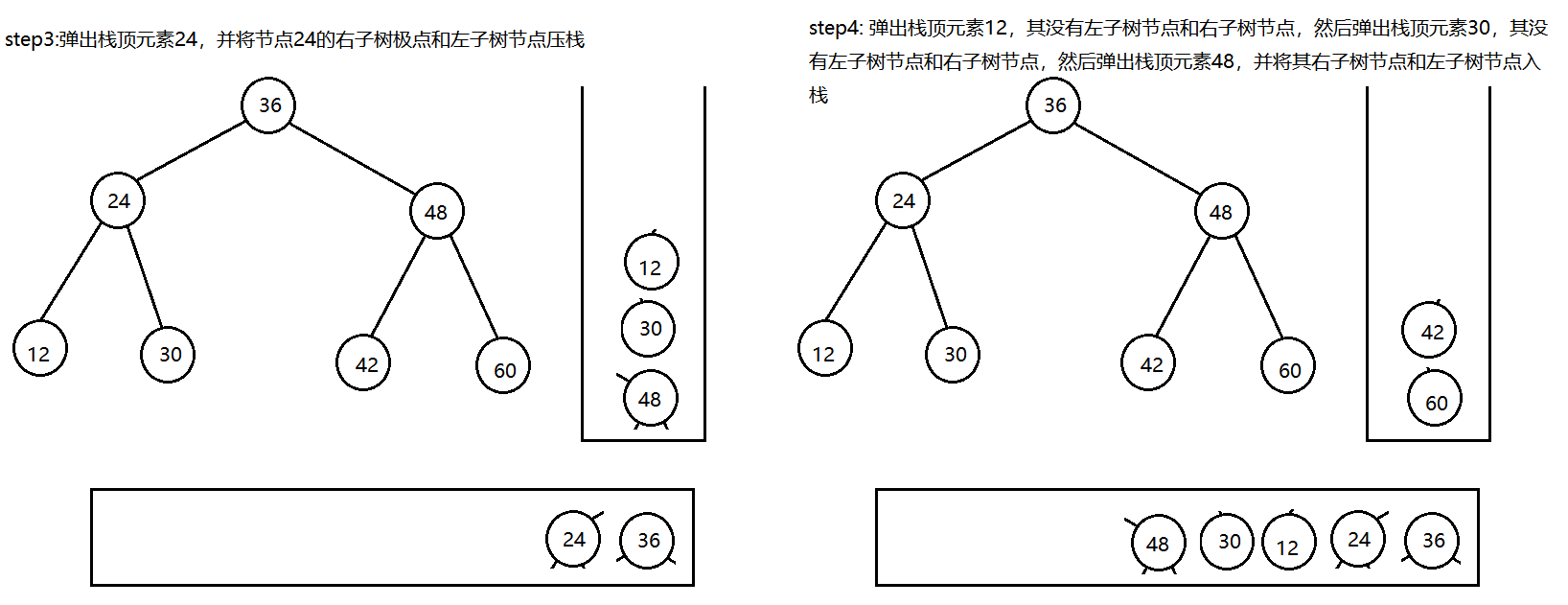
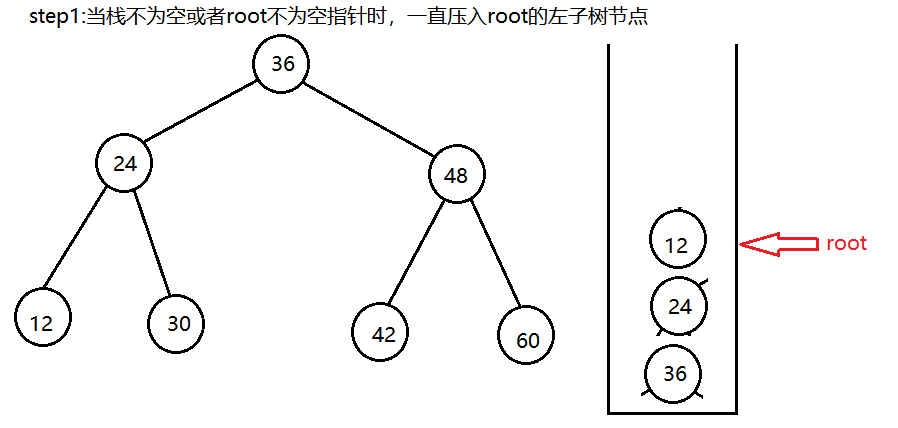
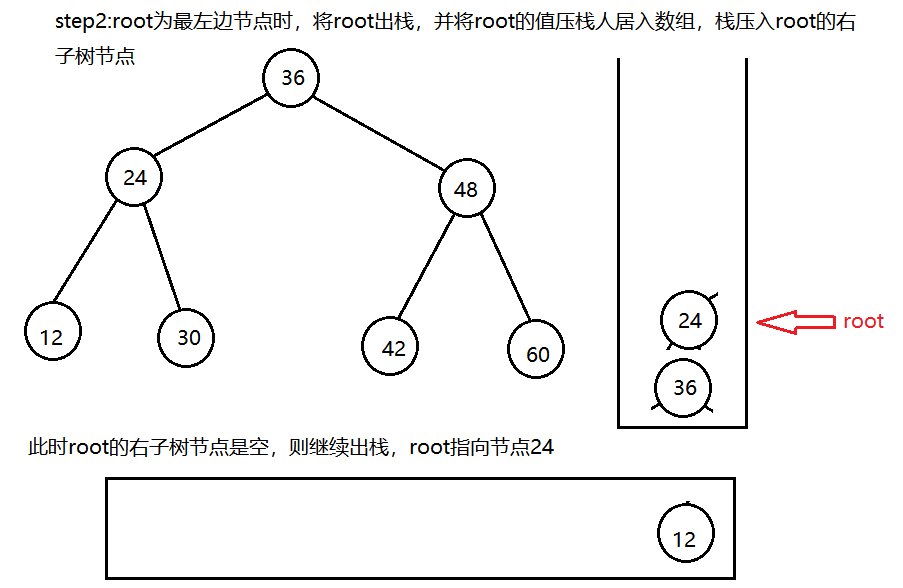
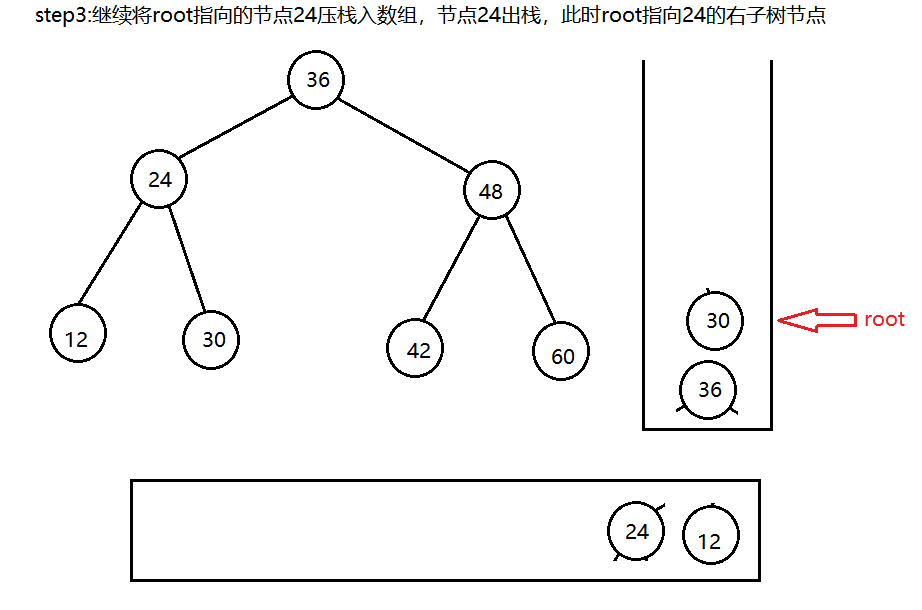
二叉树的中序遍历,即先访问左子树节点,再访问根节点,再访问右子树节点。因此要实现二叉树的中序遍历,可以借助辅助栈来实现
在二叉树的中序遍历中,每个节点会被访问两次,第一次是入栈且不输出,第二次是出栈,输出
- 代码参考
1 /** 2 * Definition for a binary tree node. 3 * struct TreeNode { 4 * int val; 5 * TreeNode *left; 6 * TreeNode *right; 7 * TreeNode(int x) : val(x), left(NULL), right(NULL) {} 8 * }; 9 */ 10 class Solution { 11 public: 12 vector<int> inorderTraversal(TreeNode* root) { 13 vector<int> B; 14 if(root==nullptr) 15 return B; 16 stack<TreeNode*> s; 17 //TreeNode* t=root; 18 while(!s.empty()||root!=nullptr) 19 { 20 while(root!=nullptr) 21 { 22 s.push(root); 23 root=root->left; 24 } 25 root=s.top(); 26 B.push_back(root->val); 27 s.pop(); 28 29 root=root->right; 30 } 31 return B; 32 } 33 };
- JAVA代码参考
1 /** 2 * Definition for a binary tree node. 3 * public class TreeNode { 4 * int val; 5 * TreeNode left; 6 * TreeNode right; 7 * TreeNode() {} 8 * TreeNode(int val) { this.val = val; } 9 * TreeNode(int val, TreeNode left, TreeNode right) { 10 * this.val = val; 11 * this.left = left; 12 * this.right = right; 13 * } 14 * } 15 */ 16 class Solution { 17 public List<Integer> inorderTraversal(TreeNode root) { 18 /* 19 二叉树的中序遍历:首先访问左子树节点,再访问根节点,最后访问右子树节点 20 可以申请一个辅助栈。当节点的左子树不为空时,一直入栈 21 当节点的右子树不为空时,将右子树压入 22 */ 23 List<Integer> list=new ArrayList<Integer>(); 24 if(root==null) 25 return list; 26 Stack<TreeNode> s=new Stack<TreeNode>(); 27 while(!s.empty()||root!=null) 28 { 29 //如果根节点的左子树节点不为空,则一直将根节点的左子树节点压入 30 while(root!=null) 31 { 32 s.push(root); 33 root=root.left; 34 } 35 root=s.peek(); 36 list.add(root.val); 37 s.pop(); 38 39 root=root.right; 40 } 41 return list; 42 } 43 }
- 问题分析
类似中序遍历,首先一直访问右子树节点,访问一个输出一个,然后弹出,若该结点存在左子树节点,则直接入栈,全部访问后将数组逆置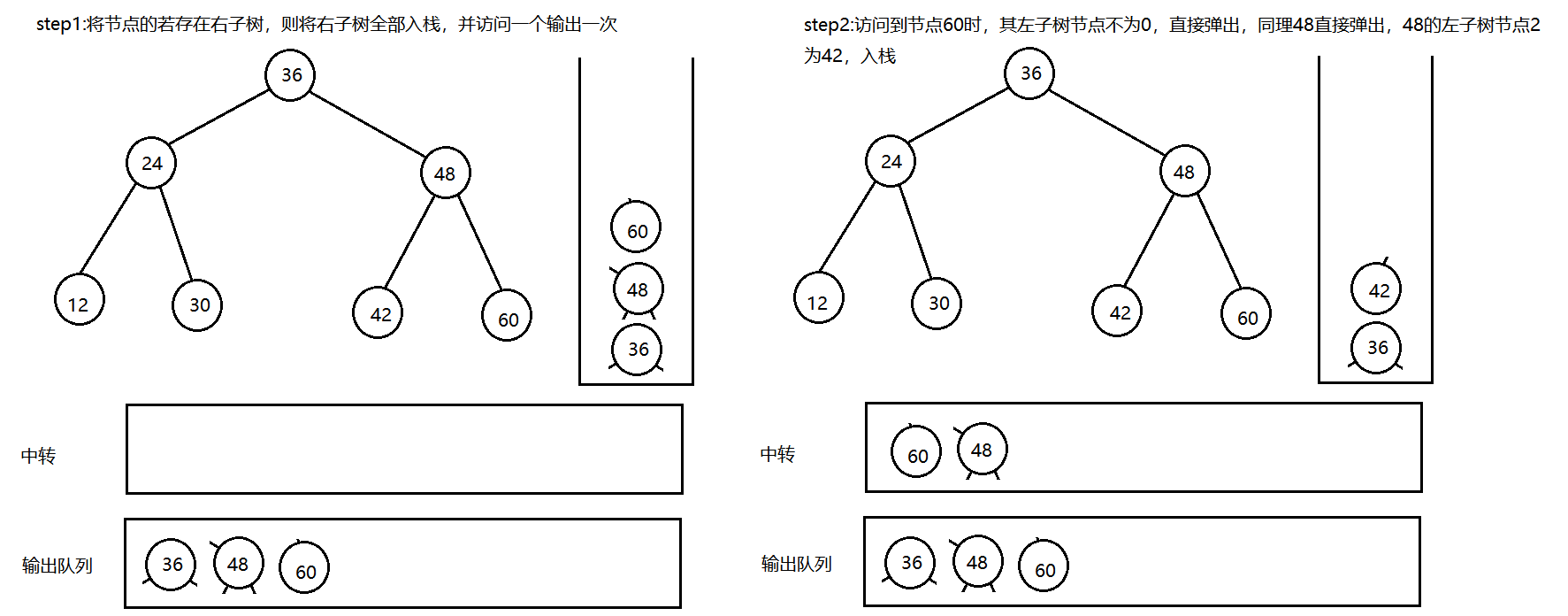
- 代码参考
1 /** 2 * Definition for a binary tree node. 3 * struct TreeNode { 4 * int val; 5 * TreeNode *left; 6 * TreeNode *right; 7 * TreeNode(int x) : val(x), left(NULL), right(NULL) {} 8 * }; 9 */ 10 class Solution { 11 public: 12 vector<int> postorderTraversal(TreeNode* root) { 13 //后序遍历顺序中每个节点被访问三次 14 //第一次: 15 vector<int> B; 16 if(root==nullptr) 17 return B; 18 stack<TreeNode*> s; 19 while(!s.empty()||root) 20 { 21 while(root!=nullptr) 22 { 23 B.push_back(root->val); 24 s.push(root); 25 root=root->right; 26 } 27 root=s.top(); 28 s.pop(); 29 root=root->left; 30 } 31 reverse(B.begin(),B.end()); 32 return B; 33 } 34 };
- JAVA代码参考
1 /** 2 * Definition for a binary tree node. 3 * public class TreeNode { 4 * int val; 5 * TreeNode left; 6 * TreeNode right; 7 * TreeNode() {} 8 * TreeNode(int val) { this.val = val; } 9 * TreeNode(int val, TreeNode left, TreeNode right) { 10 * this.val = val; 11 * this.left = left; 12 * this.right = right; 13 * } 14 * } 15 */ 16 class Solution { 17 public List<Integer> postorderTraversal(TreeNode root) { 18 ArrayList<Integer> list=new ArrayList<Integer>(); 19 if(root==null) 20 return list; 21 Stack<TreeNode> s=new Stack<TreeNode>(); 22 while(!s.empty()||root!=null) 23 { 24 //只要其存在右子树节点,则直接将右子树节点入栈 25 while(root!=null) 26 { 27 s.push(root); 28 list.add(root.val); 29 root=root.right; 30 } 31 root=s.peek(); 32 s.pop(); 33 34 35 root=root.left; 36 } 37 Collections.reverse(list); 38 return list; 39 } 40 }
- 问题分析
要实现二叉树的之字形打印,可以用两个辅助栈实现,当前排数为奇数时,从右向左压栈,否则,从左到右压栈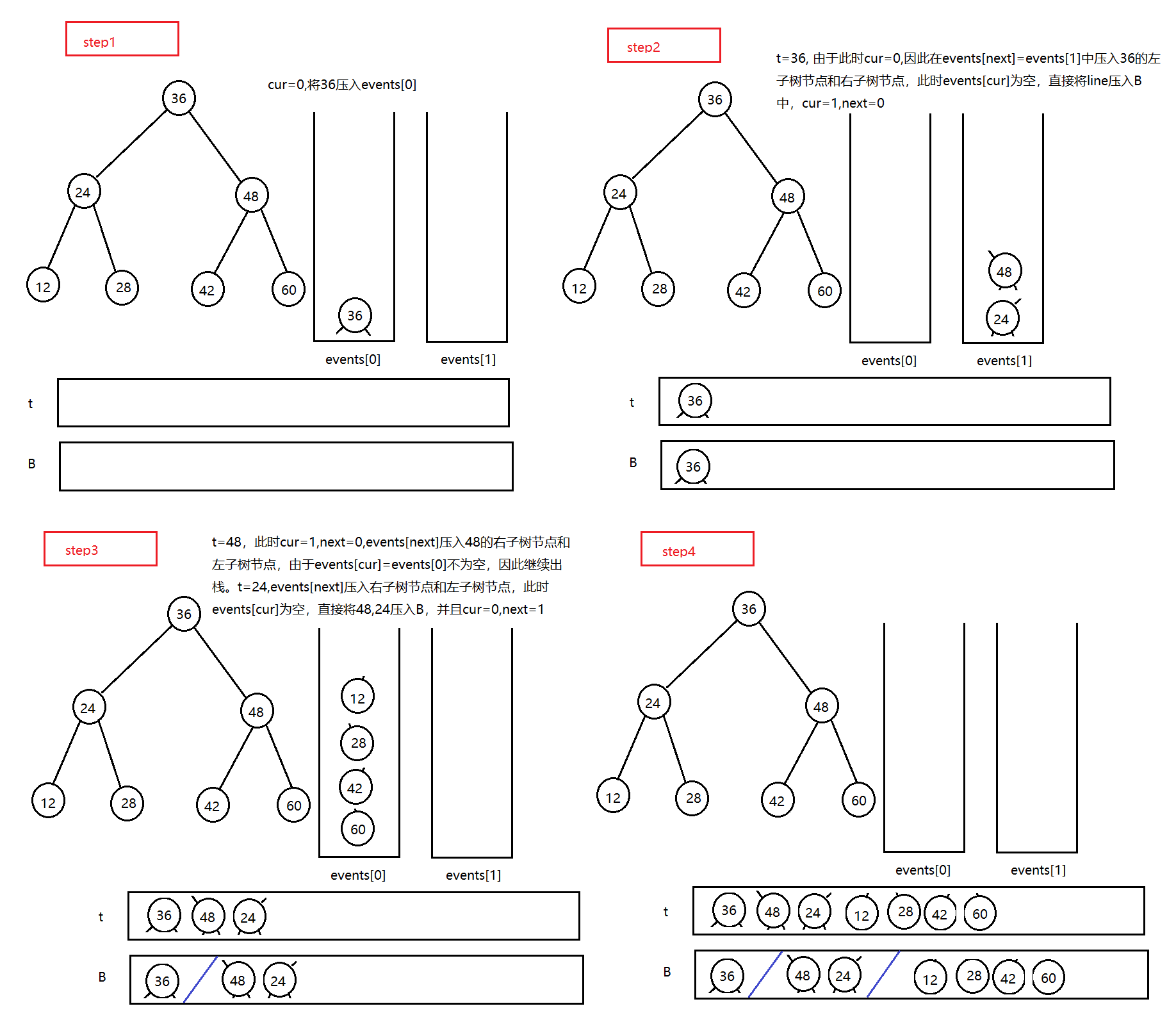

- 题目描述
1 /** 2 * Definition for a binary tree node. 3 * struct TreeNode { 4 * int val; 5 * TreeNode *left; 6 * TreeNode *right; 7 * TreeNode(int x) : val(x), left(NULL), right(NULL) {} 8 * }; 9 */ 10 class Solution { 11 public: 12 vector<vector<int>> zigzagLevelOrder(TreeNode* root) { 13 vector<vector<int>> B; 14 if(root==nullptr) 15 return B; 16 vector<int> line; 17 int cur=0; 18 int next=1; 19 stack<TreeNode*> events[2]; 20 events[cur].push(root); 21 while(!events[0].empty()||!events[1].empty()) 22 { 23 TreeNode* t=events[cur].top(); 24 line.push_back(t->val); 25 events[cur].pop(); 26 if(cur==0) 27 { 28 if(t->left) 29 events[next].push(t->left); 30 if(t->right) 31 events[next].push(t->right); 32 } 33 else 34 { 35 if(t->right) 36 events[next].push(t->right); 37 if(t->left) 38 events[next].push(t->left); 39 } 40 if(events[cur].empty()) 41 { 42 B.push_back(line); 43 line.clear(); 44 cur=1-cur; 45 next=1-next; 46 } 47 } 48 return B; 49 } 50 };
- JAVA代码参考
思路分析:使用广度优先搜索,对树进行逐层遍历,用队列维护当前的所有元素,当队列不为空时,求得当前队列的长度size,每次从队列中取出size个元素进行扩展,然后进行下一次迭代
可以利用双端队列的数据结构来维护当前层节点输出的顺序
双端队列是一个可以在任意一段插入元素的队列,广度优先搜索遍历当前层节点扩展下一层节点时我们仍从左往右按顺序扩展,但是对当前层节点的存储我们维护一个变量isLeftOrder记录是从左至右还是从右至左
- 如果从左至右,则每次将遍历到的元素插入到双端队列的末尾
- 如果从右至左,则每次将遍历到的元素插入至双端队列的头部
1 /** 2 * Definition for a binary tree node. 3 * public class TreeNode { 4 * int val; 5 * TreeNode left; 6 * TreeNode right; 7 * TreeNode(int x) { val = x; } 8 * } 9 */ 10 class Solution { 11 public List<List<Integer>> zigzagLevelOrder(TreeNode root) { 12 List<List<Integer>> list=new LinkedList<List<Integer>>(); 13 if(root==null) 14 return list; 15 Queue<TreeNode> nodeQueue=new LinkedList<TreeNode>(); 16 nodeQueue.offer(root); 17 boolean isLeftOrder=true; 18 while(!nodeQueue.isEmpty()) 19 { 20 //记录每一层节点的值 21 Deque<Integer> level=new LinkedList<Integer>(); 22 int count=nodeQueue.size(); 23 for(int i=0;i<count;++i) 24 { 25 TreeNode curNode=nodeQueue.poll(); 26 //先访问左子树节点,再访问右子树节点 27 if(isLeftOrder) 28 { 29 level.offerLast(curNode.val); 30 } 31 //否则,先访问右子树节点,再访问左子树节点 32 else 33 level.offerFirst(curNode.val); 34 35 if(curNode.left!=null) 36 nodeQueue.offer(curNode.left); 37 if(curNode.right!=null) 38 nodeQueue.offer(curNode.right); 39 } 40 list.add(new LinkedList<Integer>(level)); 41 isLeftOrder=!isLeftOrder; 42 } 43 return list; 44 } 45 }
4. 括号的匹配

- 问题分析
要判断有效的字符串,可以借助辅助栈来进行实现,从头到尾扫描字符串
-
- 如果遇到左边字符串"{ [ (",则直接将左边字符串入栈
- 如果遇到右边字符串") ] }"
- 如果栈为空,则字符串无效
- 如果栈不为空,则将栈顶元素出栈,与右字符串进行匹配
- 如果右字符串不匹配,则说明括号无效
- 如果右字符串匹配("{"和"}","["和"]","("和")"),则继续匹配下一个字符
- 扫描完整个字符串后
- 如果栈为空,则括号匹配
- 如果栈不为空,则括号不匹配
- 代码参考
1 class Solution { 2 public: 3 bool isValid(string s) { 4 /* 5 利用栈来实现 6 如果遇到左边括号{[(,则将左边字符入栈 7 如果遇到右边括号)]} 8 如果栈为空,则为无效字符 9 如果栈不为空,将栈顶字符弹出,与右边字符进行匹配 10 如果右边字符不匹配,则为无效括号 11 如果右边字符匹配,则为有效括号 12 扫描完整个字符串后 13 如果栈为空,则为有效括号 14 如果栈不为空,则为无效括号 15 */ 16 stack<char> si; 17 int len=s.length(); 18 for(int i=0;i<len;++i) 19 { 20 if(s[i]=='{'||s[i]=='['||s[i]=='(') 21 si.push(s[i]); 22 else 23 { 24 if(si.empty()) 25 return false; 26 char left=si.top(); 27 si.pop(); 28 if(left=='{'&&s[i]!='}') 29 return false; 30 if(left=='['&&s[i]!=']') 31 return false; 32 if(left=='('&&s[i]!=')') 33 return false; 34 } 35 } 36 return si.empty(); 37 } 38 };
- JAVA代码参考
1 class Solution { 2 public boolean isValid(String s) { 3 /* 4 将字符串中的字符入栈 5 若其为左边括号(,[,{,则直接将左边括号入栈 6 若其为右边括号),],} 7 若当前栈为空,则不匹配,返回fasle 8 若当前栈非空且栈顶元素与待插入字符是一对,则直接将待插入元素弹出,且指向字符串中下一个字符 9 若当前栈非空且栈顶元素与待插入字符不配套,则返回false 10 */ 11 if(s.length()==0) 12 return true; 13 int size=s.length(); 14 Stack<Character> si=new Stack<Character>(); 15 for(int i=0;i<size;++i) 16 { 17 //如果其为左边括号,则直接将左边括号入栈 18 if(s.charAt(i)=='('||s.charAt(i)=='['||s.charAt(i)=='{') 19 si.push(s.charAt(i)); 20 else 21 { 22 //如果当前栈为空,则直接返回false 23 if(si.empty()) 24 return false; 25 char left=si.peek(); 26 si.pop(); 27 if(left=='('&&s.charAt(i)!=')') 28 return false; 29 if(left=='['&&s.charAt(i)!=']') 30 return false; 31 if(left=='{'&&s.charAt(i)!='}') 32 return false; 33 } 34 } 35 return si.empty(); 36 } 37 38 }

- 问题分析
要实现字符串解码,我们可以用两个辅助栈来实现,一个辅助栈存储数字,一个辅助栈存储字符
此外,利用两个辅助变量,num保存数字,res保存字符串
算法如下
从头到尾遍历整个数组
若当前字符c为数字,则将数字字符转换为数字
若当前字符c为字母,则将字母字符添加到res后
若当前字符c为左括号[,将res和num分别入栈,并分别置空置零
记录res的临时结果res至栈,用于发现对应]后,获取timesx[....]字符
若当前字符c为有括号],将两个栈顶元素出栈,并将res中元素循环相应的nums.top()次
- 代码参考
1 class Solution { 2 public: 3 string decodeString(string s) { 4 /* 5 利用两个辅助栈来实现,一个栈存储数字,一个栈存储字符串 6 借助两个辅助变量,num来保存数字,res保存字符串 7 从头到尾遍历整个数组 8 若当前字符c为数字,则将数字字符转换为数字 9 若当前字符c为字母,则将字符c添加到res后面 10 若当前字符c为[,则将目前有的nums和res分别入栈 11 若当前字符c为],则将栈顶元素出栈,并且res中的元素循环相应的num次 12 */ 13 stack<int> nums; 14 stack<string> strs; 15 int num=0; 16 string res=""; 17 int len=s.size(); 18 for(int i=0;i<len;++i) 19 { 20 //如果为数字,则将数字字符转换为数字 21 if(s[i]>='0'&&s[i]<='9') 22 { 23 num=num*10+s[i]-'0'; 24 } 25 //如果为字符,则直接在res后面添加 26 else if((s[i]>='a'&&s[i]<='z')||s[i]>='A'&&s[i]<='Z') 27 { 28 res=res+s[i]; 29 } 30 //如果为字符[,则分别将num和res入栈,并且将num和res置零 31 else if(s[i]=='[') 32 { 33 nums.push(num); 34 num=0; 35 strs.push(res); 36 res=""; 37 } 38 //如果为字符']' 39 else 40 { 41 int times=nums.top(); 42 nums.pop(); 43 for(int j=0;j<times;++j) 44 { 45 strs.top()+=res; 46 } 47 res=strs.top(); 48 strs.pop(); 49 } 50 } 51 return res; 52 } 53 };
所谓单调栈就是自栈顶到栈底元素单调递增/递减的栈
单调栈中存放的数据是有序的,因此单调栈也分为单调递增栈和单调递减栈
-
- 单调递增栈:栈中数据出栈顺序为单调递增序列,或者说:单调递增栈从栈底到栈顶递增
- 栈为空,入栈
- 栈非空且待插入元素大于栈顶元素,入栈
- 栈非空且待插入元素小于栈顶元素,则出栈,直到待插入元素大于栈顶元素
- 单调递增栈:栈中数据出栈顺序为单调递增序列,或者说:单调递增栈从栈底到栈顶递增
单调递增栈伪代码:
for(遍历整个数组) { while(栈非空&&待插入元素<栈顶元素) { 栈顶元素出栈;
更新结果; } 待插入元素入栈; }
返回结果;
-
- 单调递减栈:栈中数据出栈顺序为单调递减序列,或者说:单调递减栈从栈底到栈顶递减
- 栈为空,则入栈
- 栈非空且待插入元素小于栈顶元素,则入栈
- 栈非空且待插入元素大于栈顶元素,则出栈,直到待插入元素小于栈顶元素
- 单调递减栈:栈中数据出栈顺序为单调递减序列,或者说:单调递减栈从栈底到栈顶递减
单调递减栈伪代码
stack<int> st; for(遍历这个数组) { while(非栈空&&栈顶元素>当前待插入元素) { 栈顶元素出栈; 更新结果; } 当前元素入栈; } 返回结果;

- 问题分析
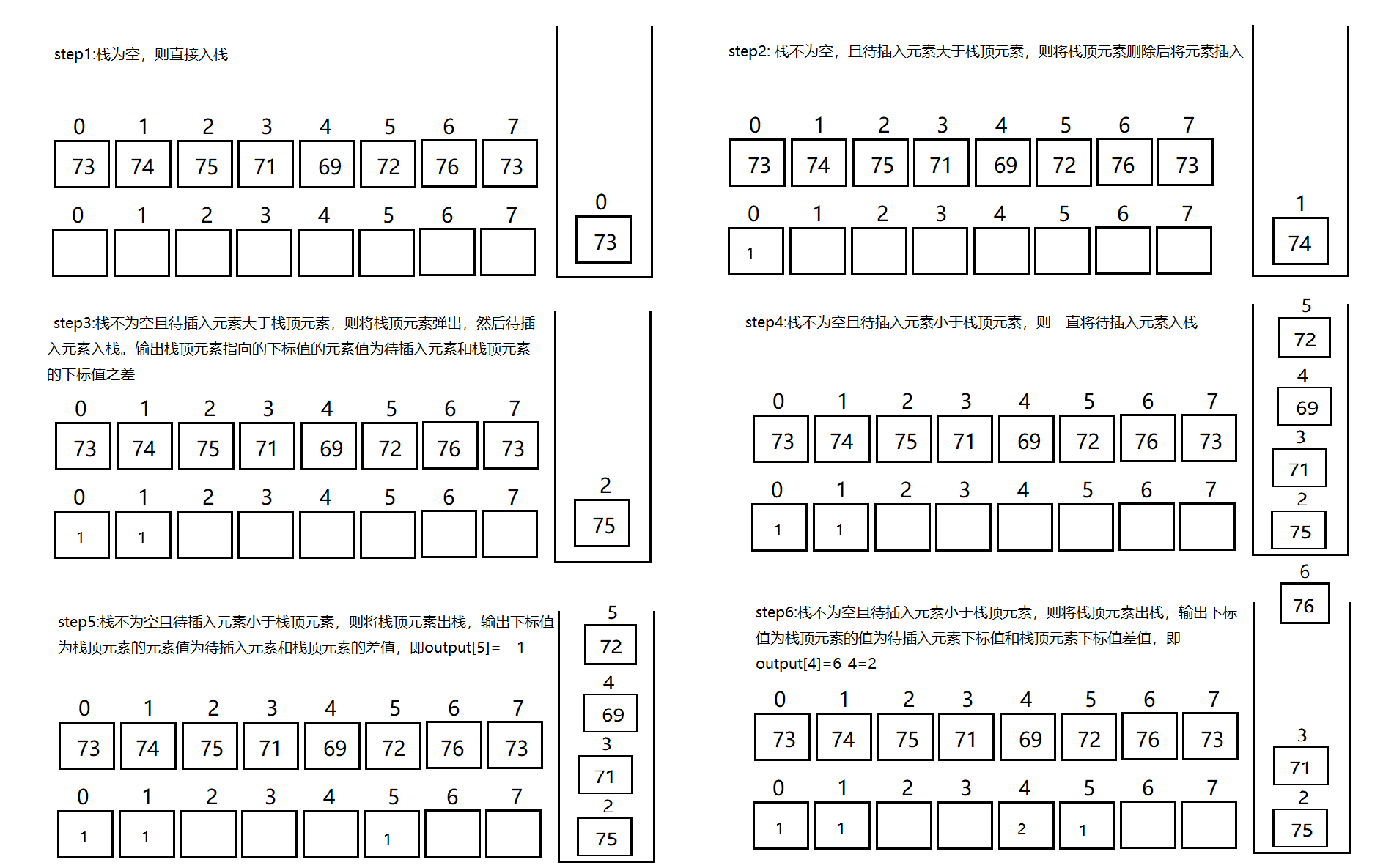
输出是至少需要等待的天数比当天气温更高,因此我们可以借助栈来实现,由于需要看天数的间隔,我们将气温的下标入栈而不是直接将气温入栈。
三种情况:
1. 如果当前栈为空,则直接将气温下标入栈
2. 如果当前栈非空并且待插入的元素小于栈顶元素,则直接将待插入的元素的下标入栈
3. 如果当前栈非空并且待插入的元素大于栈顶元素,则将栈顶元素出栈,一直到待插入的元素小于栈顶元素
- 代码参考
1 class Solution { 2 public: 3 vector<int> dailyTemperatures(vector<int>& T) { 4 /* 5 如果栈为空,则入栈 6 如果栈不为空,且待插入的元素小于栈顶元素,则直接入栈 7 如果栈不为空且待插入的元素大于栈顶元素,则一直出栈,直到待插入的元素小于栈顶元素,再出栈 8 */ 9 int len=T.size(); 10 vector<int> B(len,0); 11 if(T.empty()) 12 return B; 13 stack<int> index; 14 for(int i=0;i<len;++i) 15 { 16 //如果当前栈不为空,且待插入的元素大于栈顶元素,则一直出栈 17 while(!index.empty()&&T[i]>T[index.top()]) 18 { 19 int t=index.top(); 20 index.pop(); 21 B[t]=i-t; 22 } 23 index.push(i); 24 } 25 return B; 26 } 27 };

- 问题分析
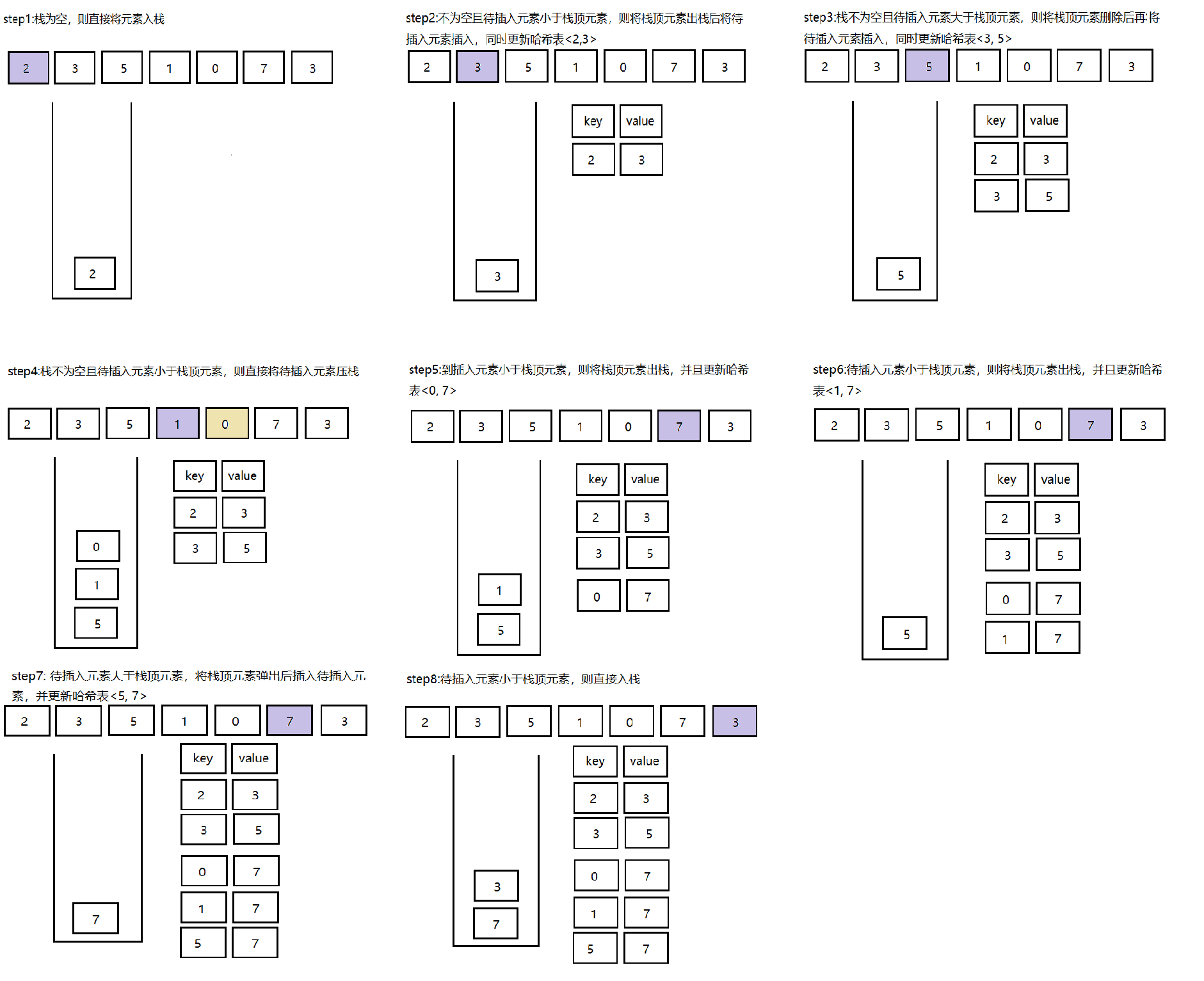
这道题我们可以利用单调栈的方法进行解决。由于nums1是nums2的子数组,因此我们先将nums2中的每个数组,求出其下一个更大的元素,并将nums2中的每个元素利用哈希表,建立nums2中的元素与其下一个更大元素之间的映射关系。再遍历nums1数组,直接找出答案。
当栈为空时,直接将nums2[i]入栈
当栈不为空时且nums2[i]<栈顶元素时,直接将nums2[i]入栈
当栈不为空且nums2[i]>栈顶元素时,将栈顶元素出栈,并建立栈顶元素和nums[i]之间对应关系的哈希表,知道nums2[i]<栈顶元素
然后遍历nums1数组,直接找出答案。
- 代码参考
1 class Solution { 2 public: 3 vector<int> nextGreaterElement(vector<int>& nums1, vector<int>& nums2) { 4 //出栈的时候更新哈希表 5 vector<int> B; 6 unordered_map<int,int> mymap; 7 stack<int> s; 8 int len=nums2.size(); 9 for(int i=0;i<len;++i) 10 { 11 while(!s.empty()&&nums2[i]>s.top()) 12 { 13 mymap[s.top()]=nums2[i]; 14 s.pop(); 15 } 16 s.push(nums2[i]); 17 } 18 while(!s.empty()) 19 { 20 mymap[s.top()]=-1; 21 s.pop(); 22 } 23 for(int i=0;i<nums1.size();++i) 24 { 25 B.push_back(mymap[nums1[i]]); 26 } 27 return B; 28 } 29 };

- 问题分析
我们可以采用单调栈来解决这个问题。
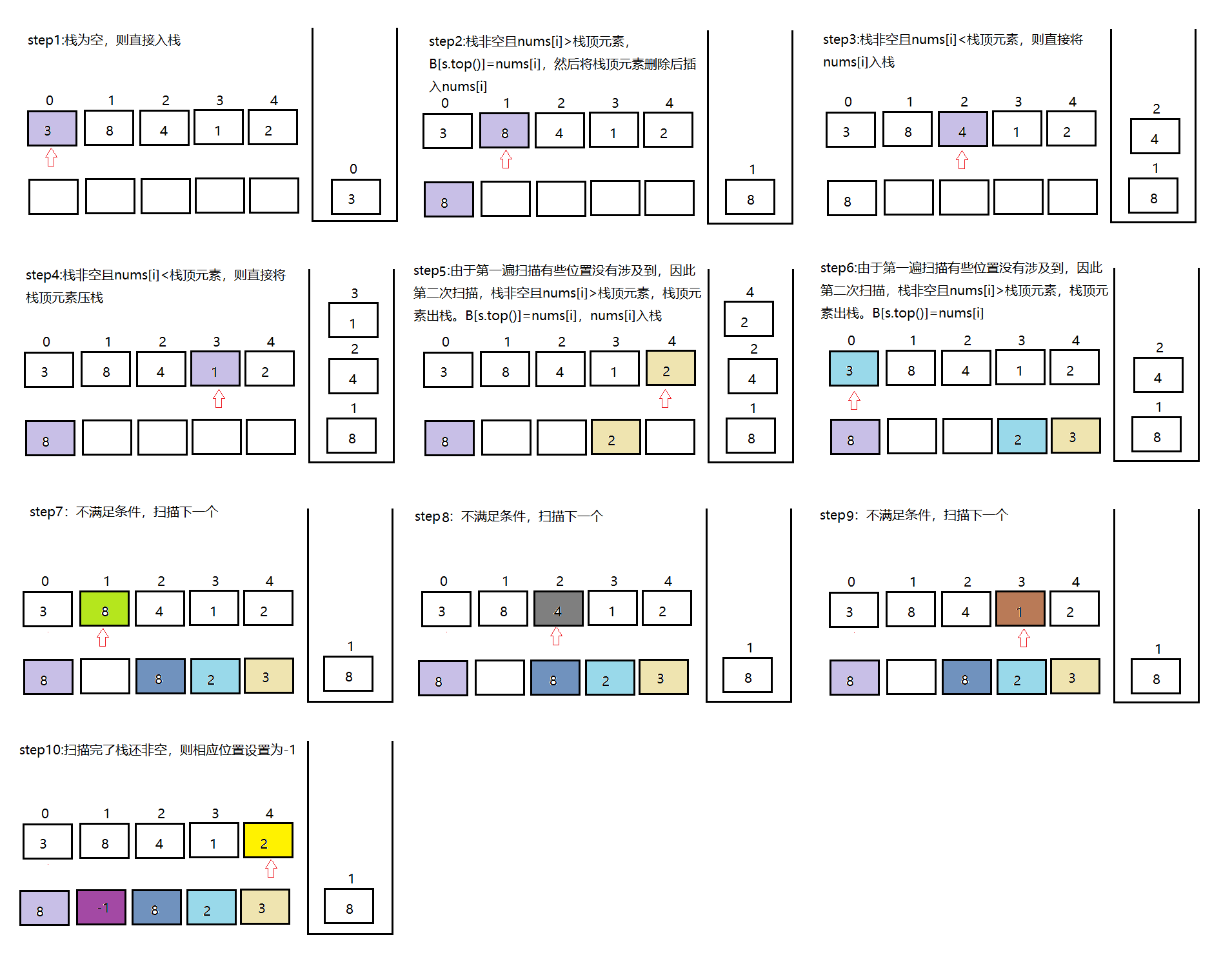
两次扫描解决循环问题
第一次扫描
如果栈为空,则当前元素nums[i]直接入栈
如果栈不为空且当前元素nums[i]<栈顶元素,则直接入栈
如果栈顶元素不为空且当前元素nums[i]>栈顶元素,则将栈顶元素出栈,且B[s.top()]=nums[i],直到当前元素nums[i]<栈顶元素,再将nums[i]入栈
第二次扫描是为了解决stack中剩下的,看是否能在前面找到更大的元素
如果栈顶元素不为空且当前元素nums[i]>栈顶元素,则将栈顶元素出栈,且B[s.top()]=nums[i]
否则直接扫描下一个元素
- 代码参考
1 class Solution { 2 public: 3 vector<int> nextGreaterElements(vector<int>& nums) { 4 int len=nums.size(); 5 vector<int> B(len,-1); 6 if(nums.empty()) 7 return B; 8 stack<int> s; 9 //两次扫描 10 for(int i=0;i<len;++i) 11 { 12 while(!s.empty()&&nums[i]>nums[s.top()]) 13 { 14 B[s.top()]=nums[i]; 15 s.pop(); 16 } 17 s.push(i); 18 } 19 //再扫描一次,处理stack中剩下的,看能否在前面找到更大的元素 20 for(int i=0;i<len;++i) 21 { 22 while(!s.empty()&&nums[i]>nums[s.top()]) 23 { 24 B[s.top()]=nums[i]; 25 s.pop(); 26 } 27 } 28 return B; 29 } 30 };

- 问题分析
采用单调栈来解决这个问题
分为两个步骤:
首先正向遍历,采用单调递增栈(从栈底到栈顶递增),找出自始至终没有出栈的最小索引l,单调递增栈特性
从栈底到栈顶递增
若栈为空,则入栈
若栈不为空且待插入元素大于栈顶元素,则直接将待插入元素入栈
若栈不为空且待插入元素小于栈顶元素,则将栈顶元素出栈,直到待插入元素大于栈顶元素
然后反向遍历,采用单调递减栈(从栈底到栈顶递减),找出自始至终没有出栈的最大索引r,单调递减栈特性
从栈底到栈顶递减
栈为空,则入栈
栈不为空且待插入元素小于栈顶元素,直接入栈
若栈不为空且待插入元素大于栈顶元素,将栈顶元素出栈,直到待插入元素小于栈顶元素
图解
正向遍历,单调递增栈
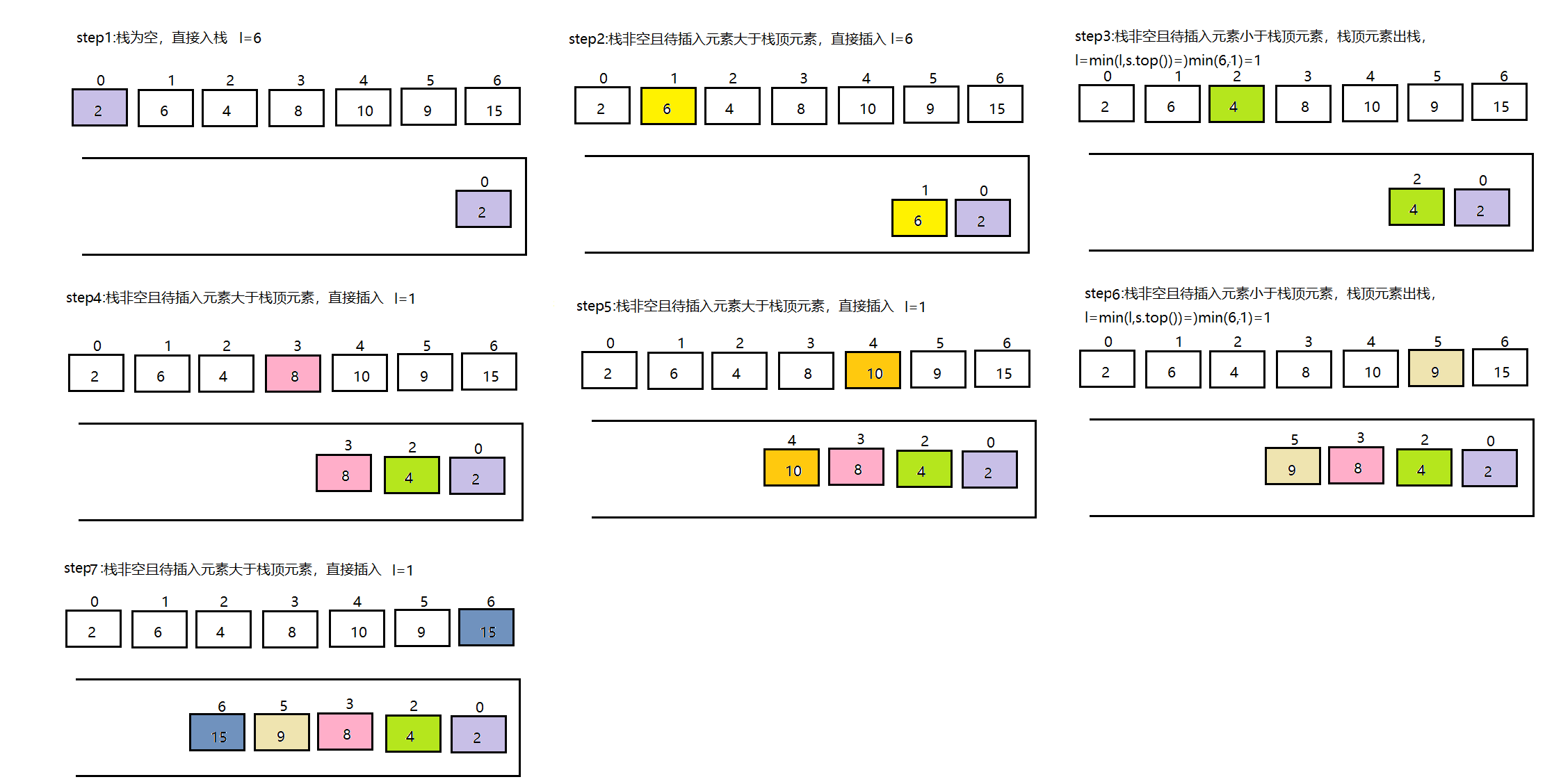
逆向遍历,单调递减栈
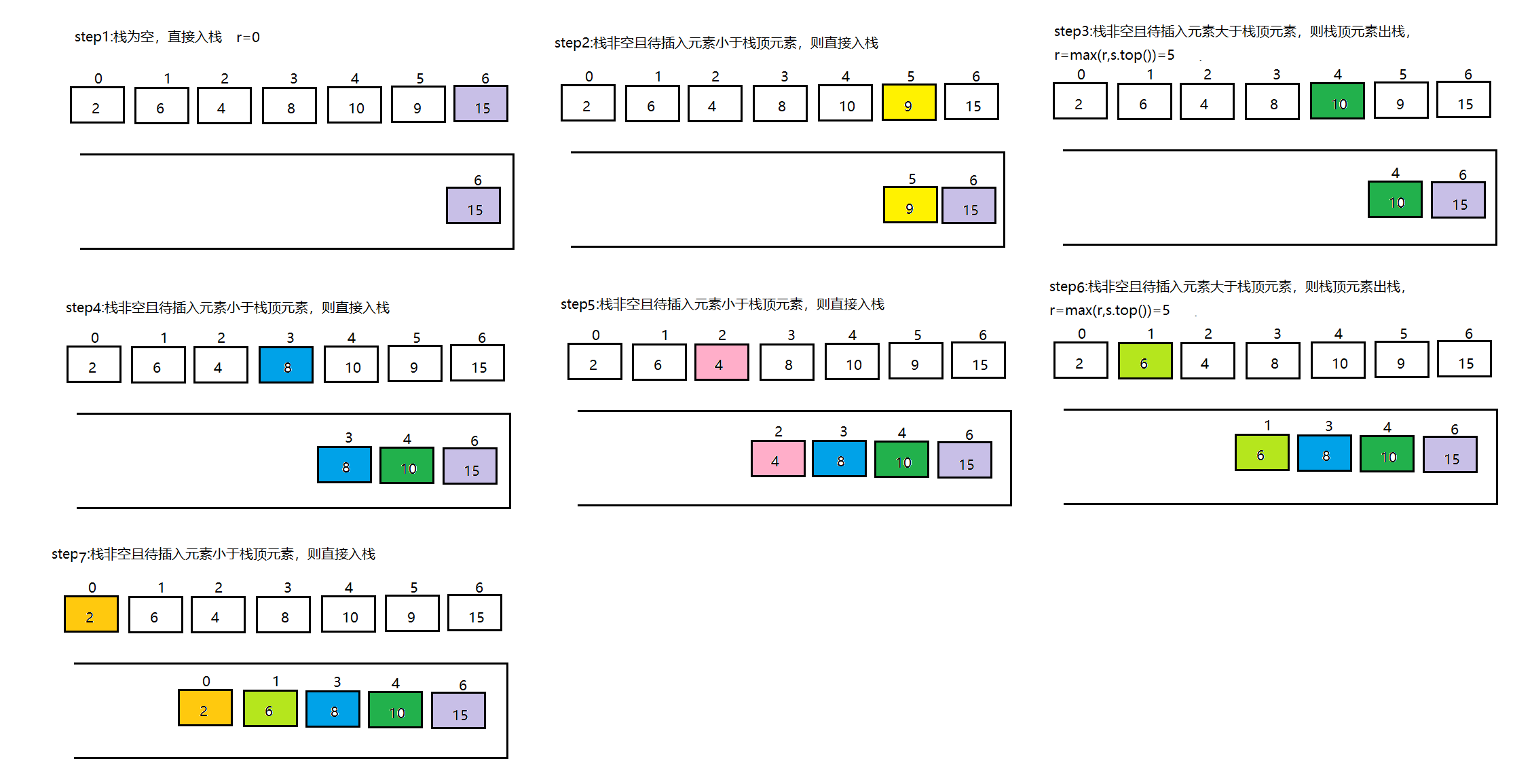
- 代码参考
1 class Solution { 2 public: 3 int findUnsortedSubarray(vector<int>& nums) { 4 stack<int> s; 5 if(nums.empty()) 6 return 0; 7 int len=nums.size(); 8 //首先正向遍历,单调递增栈,找出自始至终没有出栈的最小索引l 9 /* 10 单调递增栈:从栈底到栈顶递增 11 栈为空,入栈 12 栈不为空且待插入元素大于栈顶元素,入栈 13 栈不为空且待插入元素小于栈顶元素,出栈,直到待插入元素大于栈顶元素 14 */ 15 int l=len-1; 16 for(int i=0;i<len;++i) 17 { 18 while(!s.empty()&&nums[i]<nums[s.top()]) 19 { 20 l=min(l,s.top()); 21 s.pop(); 22 } 23 s.push(i); 24 } 25 /* 26 然后逆向遍历,单调递减栈,找到自始至终没有出栈的最大索引r 27 单调递减栈:从栈底到栈顶递减 28 栈为空,入栈 29 栈不为空且待插入元素小于栈顶元素,入栈 30 栈不为空且待插入元素大于栈顶元素,出栈直到待插入元素小于栈顶元素 31 */ 32 int r=0; 33 s=stack<int>(); 34 for(int i=len-1;i>=0;--i) 35 { 36 while(!s.empty()&&nums[i]>nums[s.top()]) 37 { 38 r=max(r,s.top()); 39 s.pop(); 40 } 41 s.push(i); 42 } 43 return (r>l)?(r-l+1):0; 44 } 45 };
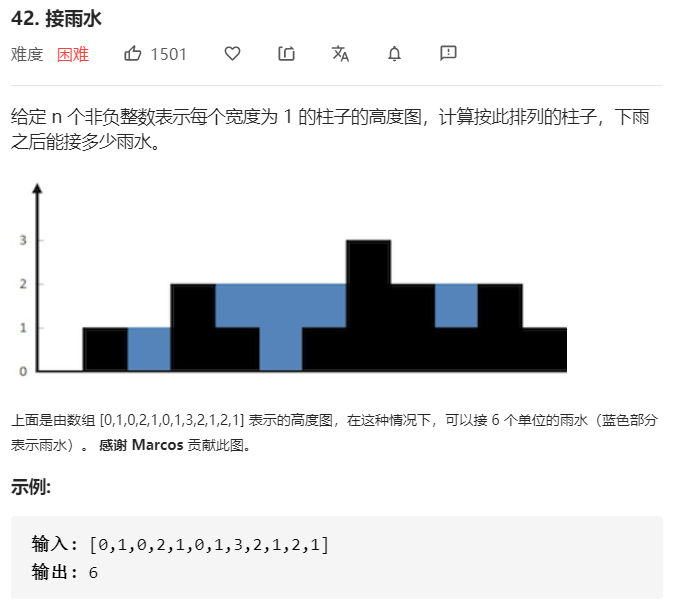
- 问题分析
我们可以使用栈来跟踪可能储水的最长的条形块,使用栈就可以依次遍历内完成计算
我们在遍历数组是维护一个单调递减栈
如果栈为空,则将数组元素入栈
如果栈非空且待插入元素小于栈顶元素,将数组元素入栈
如果栈非空且待插入元素大于栈顶元素,栈顶元素出栈,直到待插入元素小于栈顶元素。如果发现一个条形块长于栈顶,可以确定栈顶的条形状被当前条形块和栈的前一个条形块界定,因此我们可以弹出栈顶元素并且累加答案到sum
算法如下:
遍历整个数组
-
- 如果栈非空且待插入元素大于栈顶元素,即height[i]>hegiht[s.top()]
- 栈顶元素将被弹出,弹出元素即为t;
- 计算当前元素和栈顶元素的距离,准备进行填充操作
- 如果栈非空且待插入元素大于栈顶元素,即height[i]>hegiht[s.top()]
distance=i-s.top()-1;
-
-
- 找出界定高度
-
bound_height=min(height[i],height[s.top()])-height[top]
-
-
- 累加储水量sum+=distance*bound_height
- 如果当前栈为空或者待插入元素小于栈顶元素,直接将当前索引下标入栈
- 遍历下一个数组元素
-

- 代码参考
1 class Solution { 2 public: 3 int trap(vector<int>& height) { 4 if(height.empty()) 5 return 0; 6 stack<int> s; 7 int len=height.size(); 8 int sum=0; 9 for(int i=0;i<len;++i) 10 { 11 while(!s.empty()&&height[i]>height[s.top()]) 12 { 13 int t=s.top(); 14 s.pop(); 15 if(s.empty()) 16 break; 17 int distance=i-s.top()-1; 18 int bound_height=min(height[i],height[s.top()])-height[t]; 19 sum+=distance*bound_height; 20 } 21 s.push(i); 22 } 23 return sum; 24 } 25 };

- 问题分析
将滑动窗口看成一个队列,窗口滑动时,处于窗口第一个数字被删除,同时在窗口的末尾添加一个新的数字,符合队列先进先出的原则。因此采用队列来存储滑动窗口。但我们不用队列来存储滑动窗口的所有值,而是存储滑动窗口中可能最大的值。从头到尾扫描整个数组,如果当前数组元素大于滑动窗口队列中的元素,则队列中的元素不可能成为滑动窗口的最大值,将其从队尾删除;如果当前数组元素小于滑动窗口队列中的元素,则当元素从滑动窗口队列头删除后,其可能成为滑动窗口最大元素,因此将元素入

- 代码参考
1 class Solution { 2 public: 3 vector<int> maxInWindows(const vector<int>& num, unsigned int size) 4 { 5 /* 6 为了求得滑动窗口最大值,利用队列来实现,并不将滑动窗口的每个数字存入队列, 7 而是只把可能成为滑动窗口最大值的存入队列 8 */ 9 vector<int> B; 10 if(num.size()>=size&&size>=1) 11 { 12 deque<int> index; 13 int len=num.size(); 14 //首先是在滑动窗口中元素小于滑动窗口尺寸时,此时不需要判断是否滑动窗口中元素个数小于滑动窗口尺寸 15 for(int i=0;i<size;++i) 16 { 17 while(!index.empty()&&num[i]>num[index.back()]) 18 index.pop_back(); 19 index.push_back(i); 20 } 21 //当滑动窗口元素大于窗口尺寸时,此时还需要判断滑动窗口中元素个数是否小于滑动窗口尺寸,若不小于,则还需要将滑动窗口队头元素删除 22 for(int i=size;i<len;++i) 23 { 24 B.push_back(num[index.front()]); 25 while(!index.empty()&&num[i]>num[index.back()]) 26 index.pop_back(); 27 while(!index.empty()&&index.front()<=(int)(i-size)) 28 index.pop_front(); 29 index.push_back(i); 30 } 31 B.push_back(num[index.front()]); 32 } 33 return B; 34 } 35 };

- 题目描述
为了解决上述问题,即定义一个函数得到队列中的最大值,则其可以参考上述滑动窗口的最大值来解决问题,刚开始可能思考,直接定义一个队列,每次入队操作时更新其最大值

但是出队后,这个方法会造成信息丢失,即当最大值出队后,我们无法知道队列里的下一个最大值

为了解决上述问题,我们只需记住当前最大值出队后,队列中的下一个最大值即可
具体方法是使用一个双端队列dequeue,在每次入队时。如果dequeue队尾元素小于即将入队的元素,则将小于value的全部元素出队后,再将value入队,否则直接入队
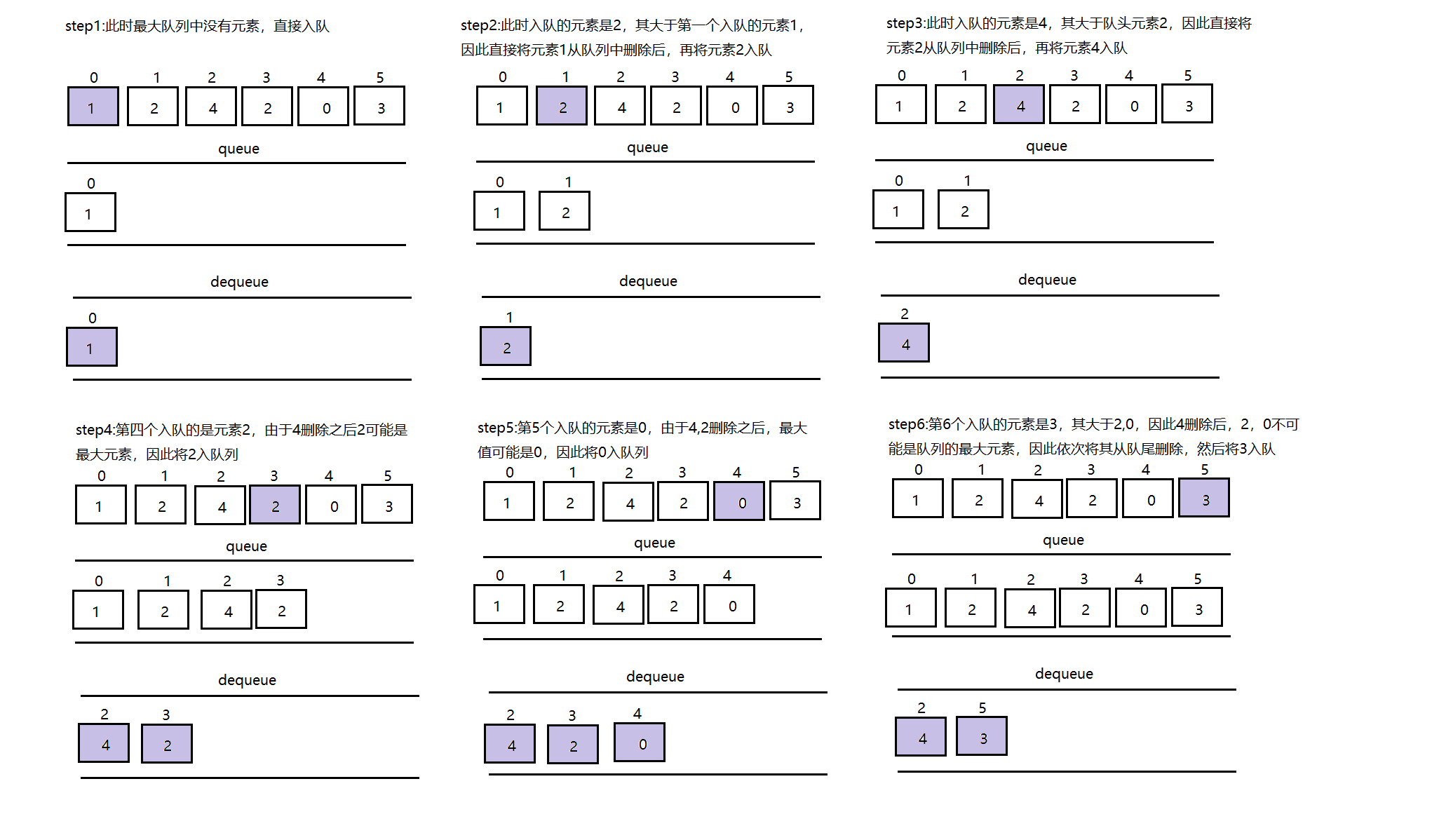
- 代码参考
1 class MaxQueue { 2 public: 3 queue<int> data; 4 deque<int> maxinums; 5 MaxQueue() { 6 7 } 8 9 int max_value() { 10 if(maxinums.empty()) 11 return -1; 12 return maxinums.front(); 13 } 14 15 void push_back(int value) { 16 while(!maxinums.empty()&&value>=maxinums.back()) 17 maxinums.pop_back(); 18 data.push(value); 19 maxinums.push_back(value); 20 } 21 22 int pop_front() { 23 if(data.empty()) 24 return -1; 25 int ans=data.front(); 26 if(ans==maxinums.front()) 27 maxinums.pop_front(); 28 data.pop(); 29 return ans; 30 } 31 32 }; 33 34 /** 35 * Your MaxQueue object will be instantiated and called as such: 36 * MaxQueue* obj = new MaxQueue(); 37 * int param_1 = obj->max_value(); 38 * obj->push_back(value); 39 * int param_3 = obj->pop_front(); 40 */
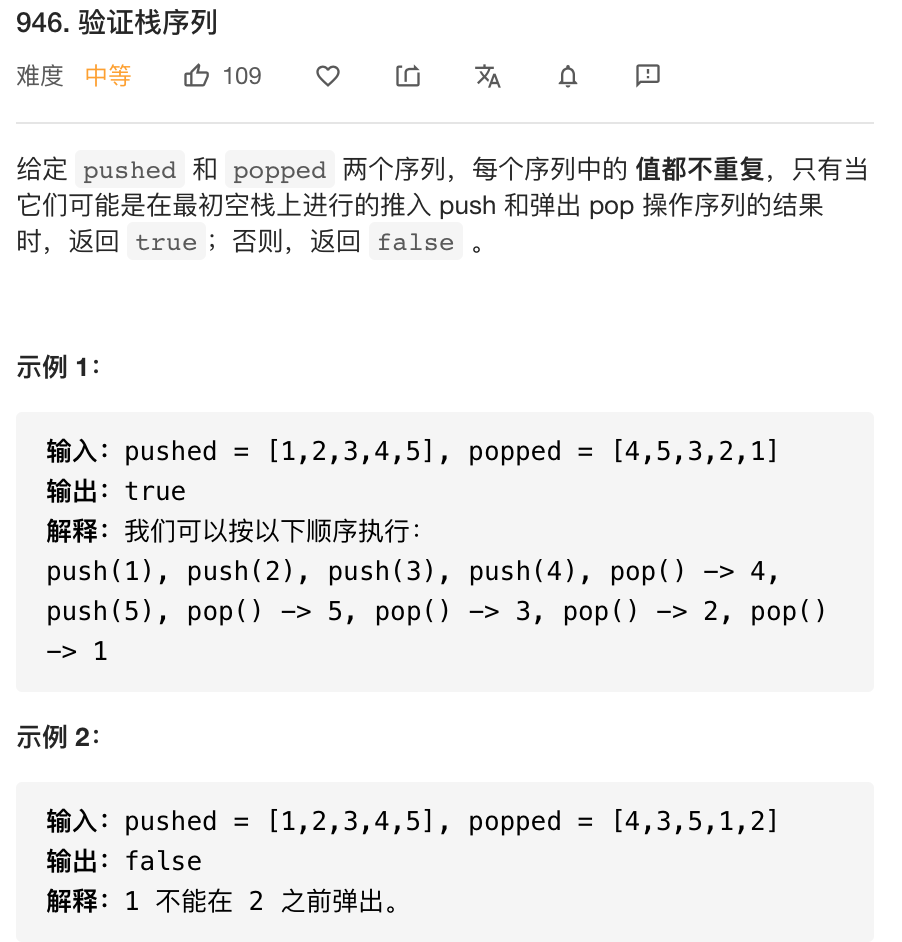
- 问题分析
要判断序列是否是栈的弹出序列,可以借助辅助栈来进行实现
定义一个辅助栈
遍历pushed数组
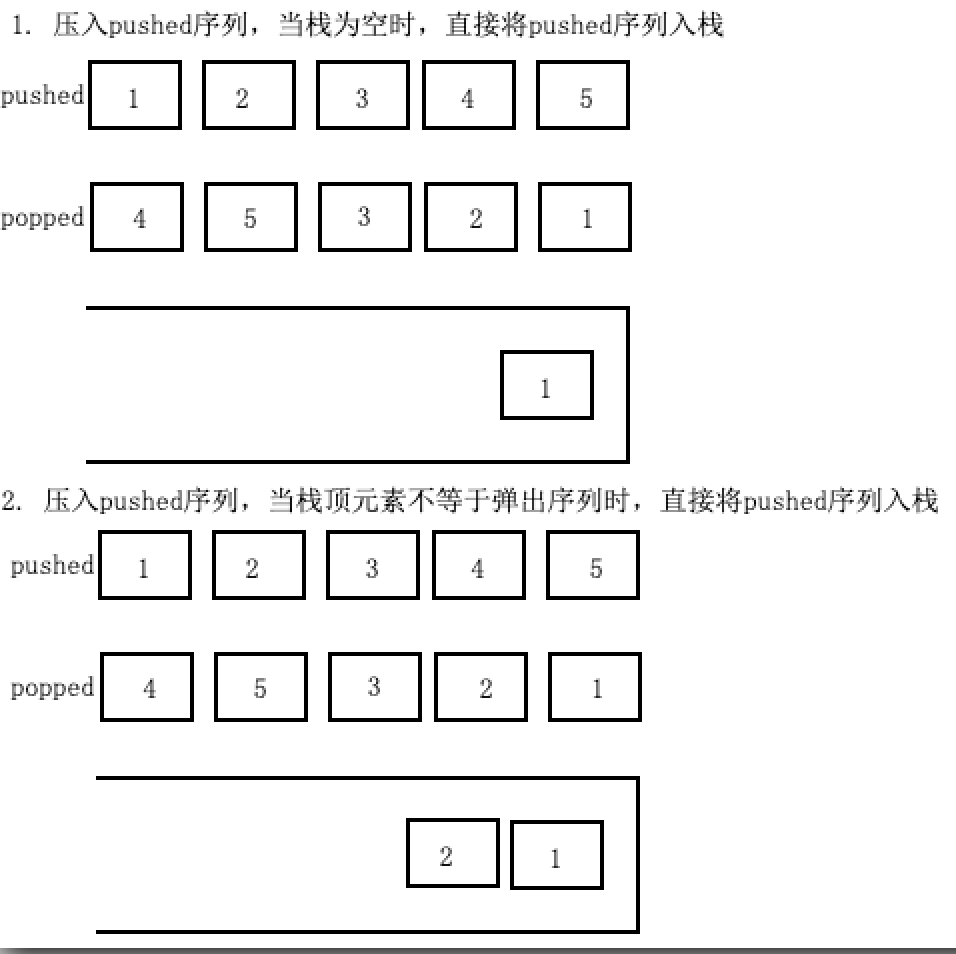
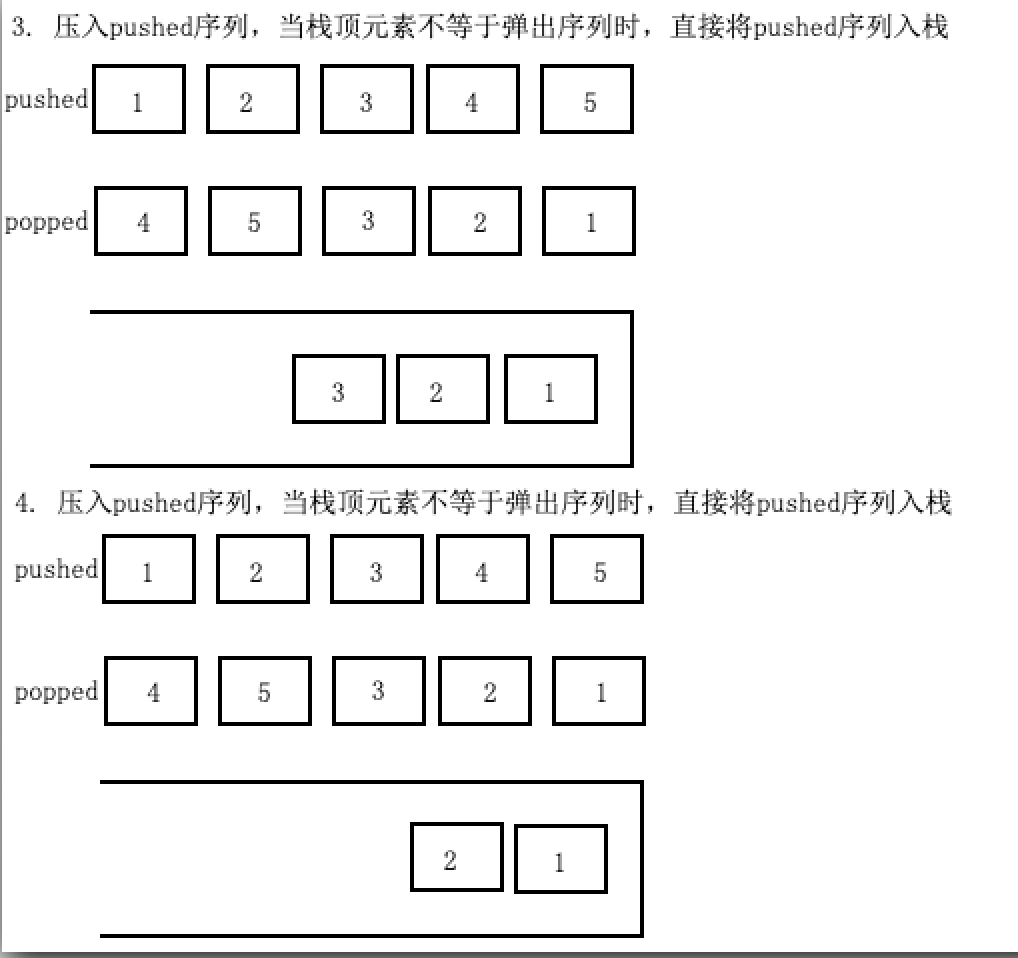
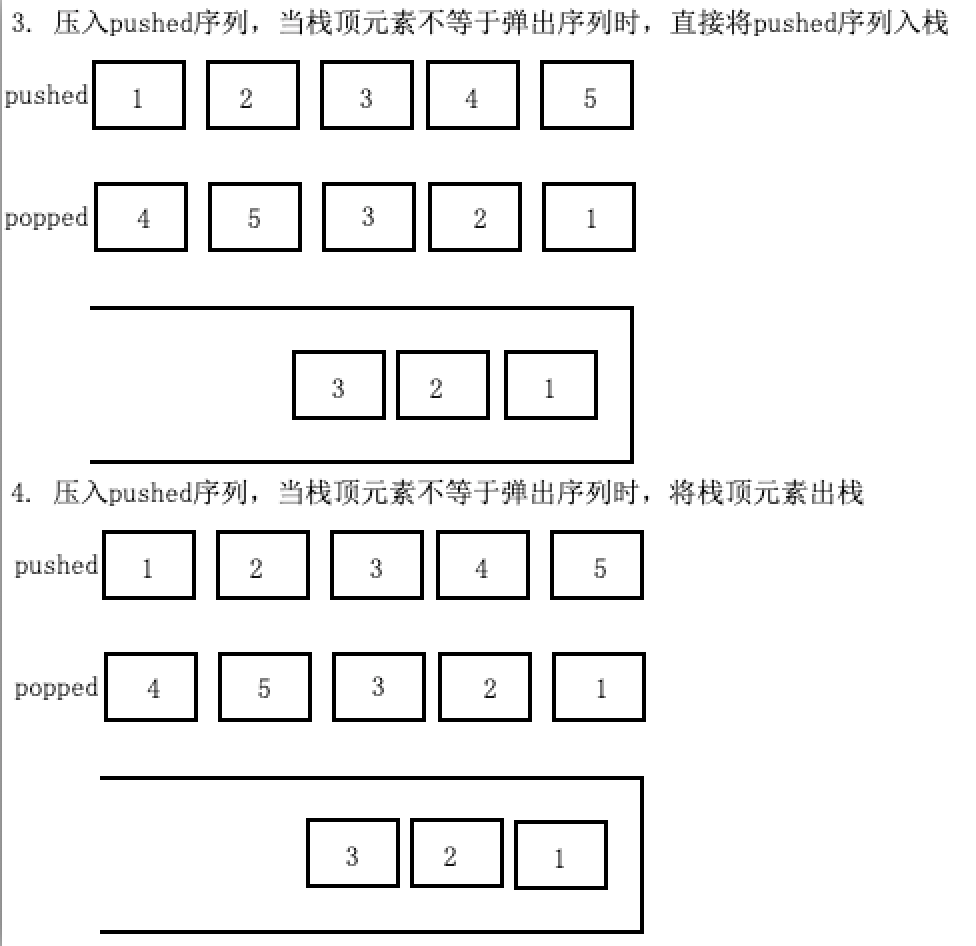
若栈为空,则将pushed数组中元素入栈
若栈不为空且栈顶元素不等于popped第一个元素,则入栈
若栈不为空且栈顶元素等于popped第一个元素,则将栈顶元素出栈
- 代码参考
1 class Solution { 2 public: 3 bool validateStackSequences(vector<int>& pushed, vector<int>& popped) { 4 stack<int> s; 5 int len=pushed.size(); 6 //栈为空,入栈 7 //栈不为空且弹出序列不等于栈顶元素,入栈 8 //栈不为空且弹出序列等于栈顶元素,将栈顶元素出栈 9 int j=0; 10 for(int i=0;i<len;++i) 11 { 12 s.push(pushed[i]); 13 while(!s.empty()&&s.top()==popped[j]) 14 { 15 s.pop(); 16 ++j; 17 } 18 } 19 return s.empty(); 20 } 21 };