bzoj1272 Gate Of Babylon（计数方法+Lucas定理+乘法逆元）

Description

 

Input

 

Output

 

Sample Input

2 1 10 13

3

Sample Output

12

 

Source

 

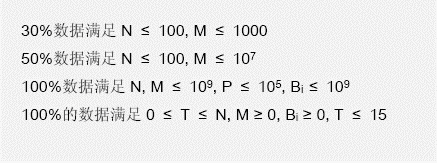
 看到t很小，想到用容斥原理，推一下发现n种数中选m个方法为C(n+m,m)。然后有的超过的就是先减掉b[i]+1，再算。由于n,m较大，p较小，故可用Lucas定理+乘法逆元搞。

把老师给的题解也放在这吧：

首先，看到有限制的只有15个，因此可以考虑使用容斥原理：Ans=全部没有限制的方案-有1个超过限制的方案数+有2个超过限制的方案数-有3个超过限制的方案数…。以此类推。我们先考虑没有限制的，在m组无限制的数中选n个的方案数，显然就是C(n+m-1,n)，因为这道题是要求不超过m的方案数，也就是那么运用加法原理发现答案也就是C(n+0-1,0)+C(n+1-1,1)+C(n+2-1,2)+...+C(n+m-1,m)=C(n+m,m)，然后考虑有限制的情况，有一个超过限制直接用总数减去（这个的限制+1)就是当前的总数，相当于强制要选限制+1个为空。然后只要DFS，记录到当前为止选了几个，答案要记是b[i]+1,判断加减，最后累加答案。最后，n、m过大，发现p是一个质数，所以可以用Lucas定理，Lucas(n,m,p)=Lucas(n/p,m/p,p)*C(n%p,m%p)，其中C(n%p,m%p)求的时候要用到乘法逆元。

program babylon(input,output);
var
  t,i:longint;
  ans,n,m,j,p:int64;
  b:array[0..20]of int64;
  a:array[0..100010]of int64;
function pow(x,y:int64):int64;
begin
   pow:=1;
   while y>0 do
      begin
         if y mod 2=1 then pow:=pow*x mod p;
         x:=x*x mod p;
         y:=y>>1;
      end;
end;
function z(n,m:int64):int64;
begin
   if n<m then exit(0);
   exit(a[n]*pow(a[n-m]*a[m] mod p,p-2) mod p);
end;
function c(n,m:int64):int64;
begin
   if n<m then exit(0);
   c:=1;
   while (n>0) and (m>0) do
      begin
         c:=c*z(n mod p,m mod p) mod p;
         n:=n div p;m:=m div p;
      end;
end;
procedure dfs(k:longint;r,s:int64);
begin
   if k=t+1 then
      begin
         ans:=(ans+r*c(n+m-s,n)) mod p;
         exit;
      end;
   dfs(k+1,r,s);
   dfs(k+1,-r,s+b[k]+1);
end;
begin
   assign(input,'babylon.in');assign(output,'babylon.out');reset(input);rewrite(output);
   readln(n,t,m,p);
   for i:=1 to t do read(b[i]);
   a[0]:=1;j:=0;
   while j<p do begin inc(j);a[j]:=a[j-1]*j mod p; end;
   ans:=0;
   dfs(1,1,0);
   if ans<0 then ans:=ans+p;write(ans);
   close(input);close(output);
end.