什么是机器学习?
机器学习:研究如何通过计算的手段,利用经验来改善系统自身的性能。
机器学习分为监督学习和非监督学习。
-
监督学习 (Supervised learning)
从给定的训练数据集中学习出一个函数(模型参数),当新的数据到来时,可以根据这个函数预测结果。监督学习的训练集要求包括输入输出,也可以说是特征和目标。
常见的有监督学习算法:回归分析和统计分类

- 非监督学习 (Unsupervised learning)
输入数据没有被标记,也没有确定的结果。样本数据类别未知,需要根据样本间的相似性对样本集进行分类(聚类,clustering)试图使类内差距最小化,类间差距最大化。
在实际应用中,不少 情况下无法预先知道样本的标签,也就是说没有训练样本对应的类别,因而只能从原先没有样本标签的样本集开始学习分类器设计。
线性回归
在对机器学习这门学科有了一个基本的认识后,我们就要正式开始进行模型算法的学习了。
在线性回归这部分,这篇博客主要从以下几个部分来讨论:
- 模型定义
- 损失函数
- 参数估计
以下笔记来自吴闻达老师的机器学习视频。
模型定义
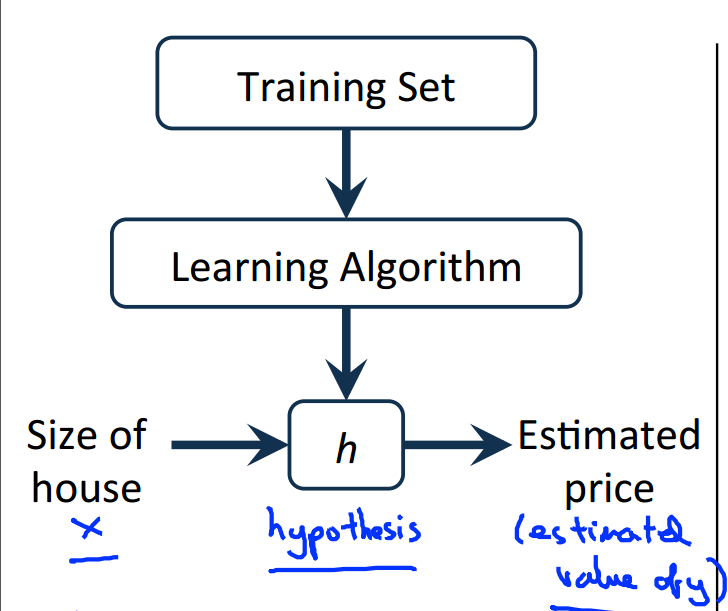
以上是监督学习问题的图示描述,我们的目标是,给定训练集,学习函数h:X→Y,使得h(x)是对于y有较好的预测值。
h(x)代表的是一个假设集合(Hypothesis ),我们要做的就是从这个假设集合中找出预测效果最好的那一个假设。

损失函数(Cost Function)
之前举的例子,关于房价的预测问题,是一个单变量的回归问题,输入数据只有x维度为1,
我们建立的模型是![]() ,我们的目标是让这个直线尽可能的拟合所有数据,
,我们的目标是让这个直线尽可能的拟合所有数据,
即从数据的中心穿过,让我们的每个预测值h(x)与我们的已知数值y尽可能的接近。
那么,我们应该怎么选择最好的模型呢?通过求解参数theta1和theta2.
我们可以通过使用 cost function(损失函数)来测量我们的假设的准确性。 这需要使用来自x的输入
和实际输出y的假设的所有结果的平均差(实际上是平均值的更好的版本),如下。
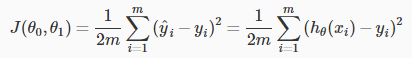
说明:其实损失函数 J 计算的是h(x)与真实值y之间的垂直距离的平方和均值。
关于为什么多一个1/2的问题,是为了以后求导方便,不用太在意这个。

为了问题描述的方便,首先使用上图右边的简单模型,只有一个参数theta1.
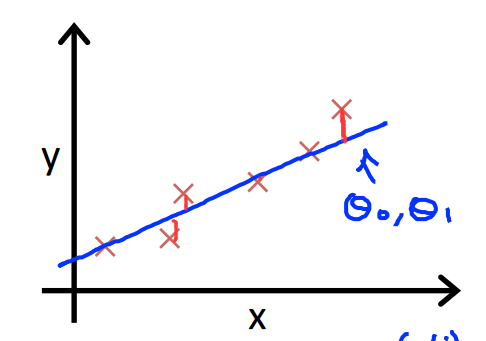
下图是对数据样本点”X“的拟合状态,
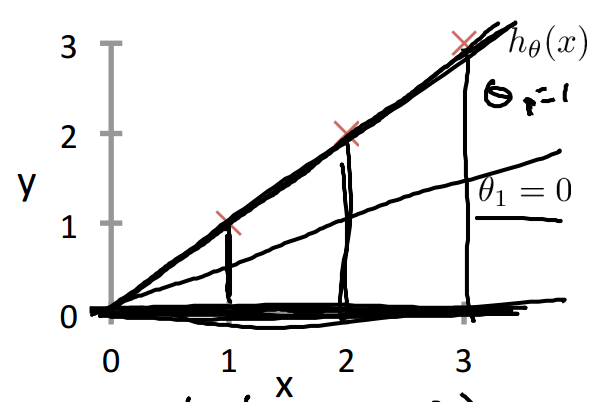
当在上图中我们随意旋转h(x),将会得到不同的 J 值,可以得到下面的关于theta1 损失函数 J 的图像:
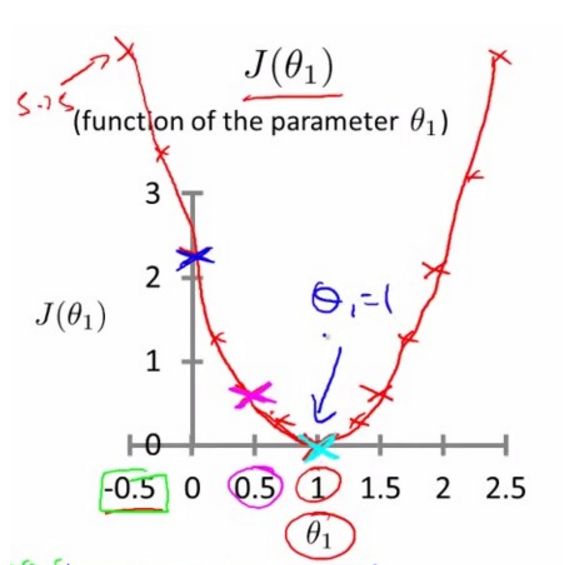
当同时考虑两个参数值 theta1和theta0时,损失函数的图像是这样的,被称为bowl-shape function,碗状的
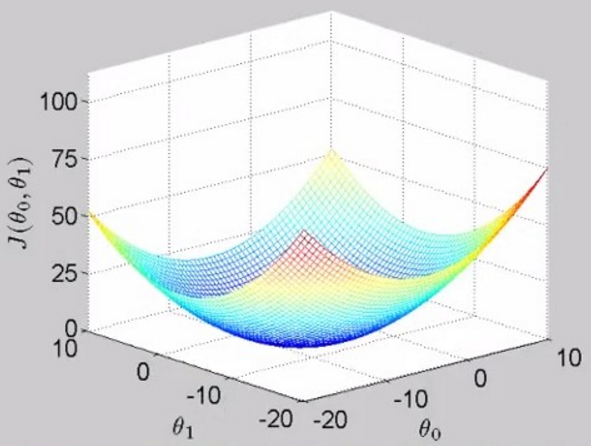
下图的右边是上面三维图像的二维展示,那一圈一圈的椭圆被称为“等高线”(类似地理上的等高线),每一个椭圆上的不同点的 J 值都是相等的,
如图中绿色椭圆上的三个点,越靠近中心的椭圆 J 值越小。
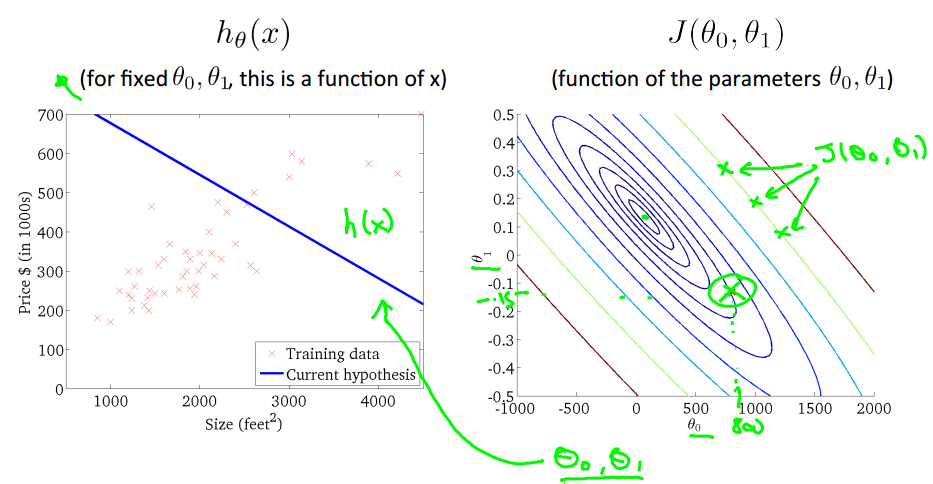
上面左图对应的是右图中用绿色圆圈标注的点(theta1=800,theta0=-1.5),对应的模型h(x)的图像,右图中每一个不同的点,
都会在左图中对应一个不同的图像,如下:
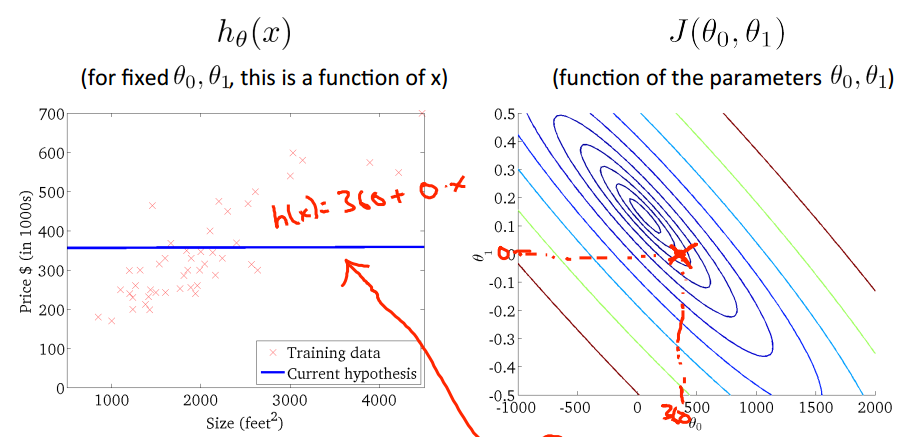
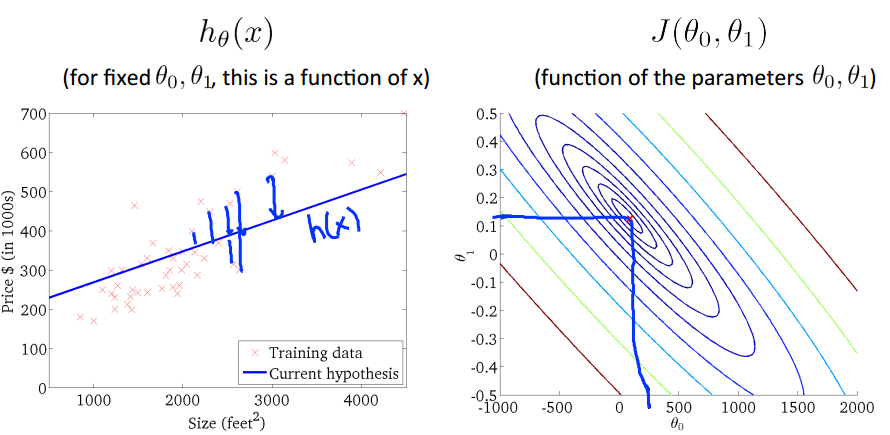
当然,我们理想的情况是类似上图的情况,我们取的(theta1,theta0)出现图中的中心theta0=450,theta1=0.12,
在这个点可以是损失函数达到最小,趋近于0.这样我们就求得了模型参数theta0和theta1,进而得到最佳的假设h(x)。
参数估计:
Gradient Descent(梯度下降)
我们有了假设模型h(x),和损失函数 J,现在来讨论如何求得theta1和theta0的方法,梯度下降。我们的问题描述如下:

需要不断迭代,求得使损失函数 J 达到最小的theta1和theta0.
关于梯度下降的理解:
假设你现在站在两座山包上的其中一座,你需要以最快的速度下到山的最低处。每到达一个新的地方,
都选择在该点处梯度最大的方向下山即可。如图:
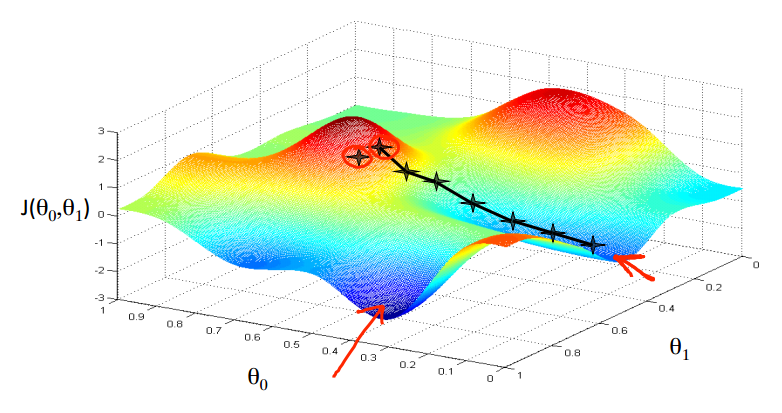
梯度下降算法表示如下:其中标出了梯度(蓝框内)和学习率(α > 0),梯度在这里通俗的说就是函数 J 的偏导数。
注意:梯度下降算法对局部最小值敏感,梯度下降可能收敛在局部最小,不能保证收敛到全局最小值。

说明:在计算机科学中,x:=x+y表示,先计算x+y的结果再赋值给变量x,类似先计算a=x+y,然后使x的值等于a。
下图为梯度为正、负的情况,theta的更新是不一样的:
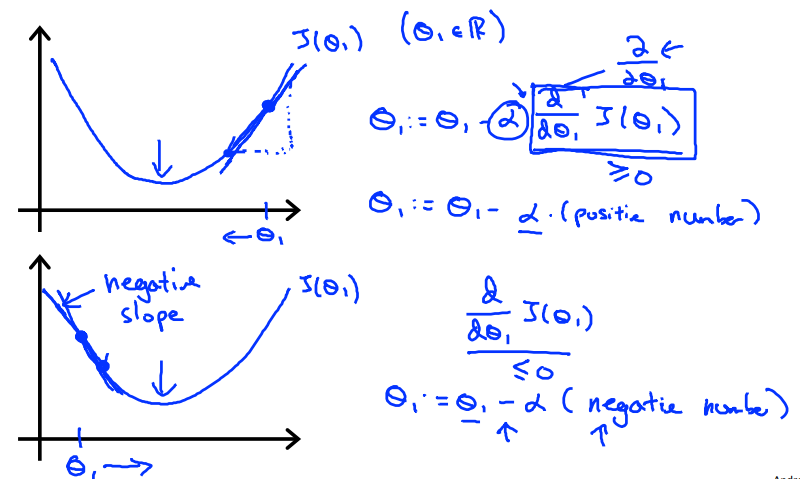
关于参数更新的问题,theta1和theta2必须同时更新,下图左边为正解,即不能使用更新过后的theta0来进一步更新theta1
(这将是后面要讲到了另一种算法)。

关于学习率α的问题:
当a过小的时候,迭代步长太小,梯度下降得太慢;
当a过大的时候,迭代步长过大,梯度无法收敛到最小值,而发生左右震荡的现象。
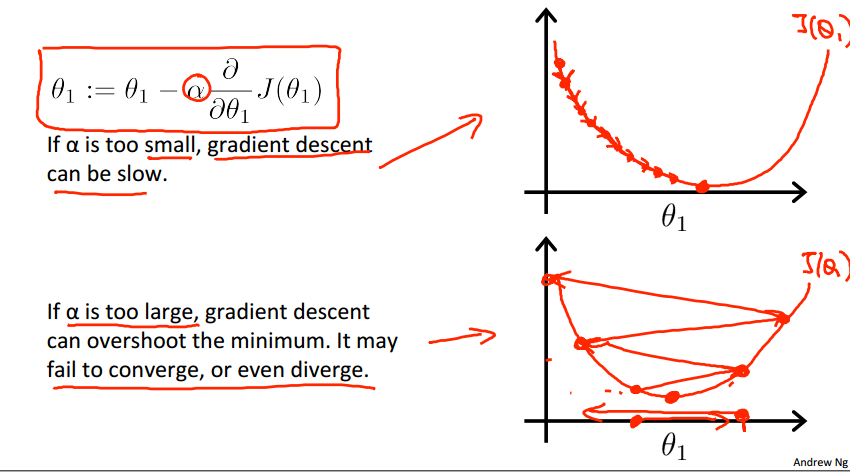
当固定a时,梯度下降法依然可以收敛到最小值(局部),
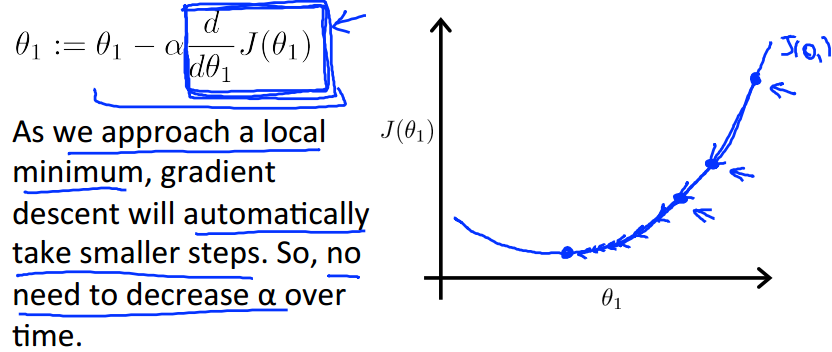
因为,当我们越靠近最小值时,我们的 梯度 越小,反应在上图就是越来越平缓,所以上面蓝色方框中的表达式会越来越小,
然后乘上a也越来越小,证明我们迭代的步长会逐步变小,即使我们使用的是固定不变的学习率a。
Gradient Descent For Linear Regression
(在线性回归中使用梯度下降)

其推导过程如下,分别对 J 求 关于theta0和theta1的偏导数:
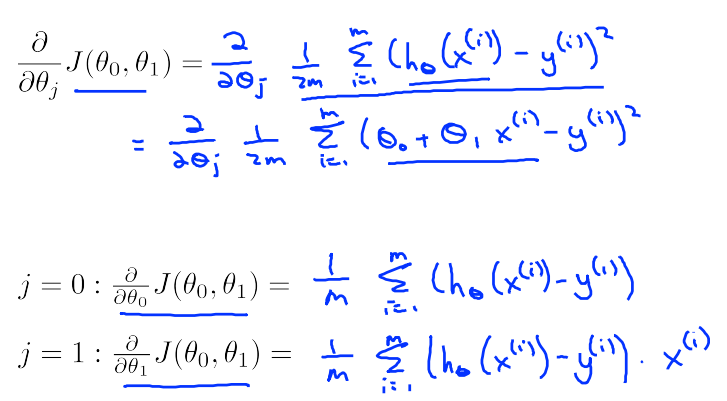
得到下面应用于线性回归的梯度下降算法:

通过对以上算法的不断迭代,我们求得了最好的假设h(x),其中红色“x”的轨迹,就是算法迭代的过程。

在参数估计这部分,视频中主要介绍了梯度下降的方法。在周志华老师《机器学习》这本书中还提到了另一种常用方法:“最小二乘法”
最小二乘法
最小二乘:它的主要思想就是找到一组参数,使得理论值与观测值之差的平方和达到最小:
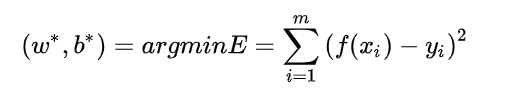
最小二乘法的参数求解:

与梯度下降方法比,最小二乘法的计算量是很大的,其局限性,主要表现在以下几个方面:
① 最小二乘法需要计算 的逆矩阵,有可能它的逆矩阵不存在,这样就没有办法直接用最小二乘法了(在这种情况下就要用到梯度下降法)。当然,还可以通过对样本数据进行整理,去掉冗余特征。让 行列式不为0,然后继续使用最小二乘法。
② 当样本特征n非常的大的时候,计算 的逆矩阵是一个非常耗时的工作,甚至不可行。此时以梯度下降为代表的迭代法仍然可以使用。但可以通过主成分分析降低特征的维度后再用最小二乘法。
③ 如果拟合函数不是线性的,这时无法使用最小二乘法,需要通过一些技巧转化为线性才能使用,此时梯度下降仍然可以用。
④ 当样本量m很少,小于特征数n的时候,这时拟合方程是欠定的,常用的优化方法都无法去拟合数据。当样本量m等于特征说n的时候,用方程组求解就可以了。当m大于n时,拟合方程是超定的,在这种情况下,最小二乘法是最常用的。
下面是我作为一个Python初学者,用Python的Scipy库照着求解最小二乘法的求解代码模板敲的:
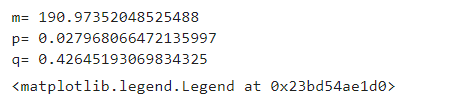
from math import e # 引入自然数e import numpy as np # 科学计算库 import matplotlib.pyplot as plt # 绘图库 from scipy.optimize import leastsq # 引入最小二乘法算法 # 样本数据(Xi,Yi),需要转换成数组(列表)形式 ti = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10]) yi = np.array([8, 11, 15, 19, 22, 23, 22, 19, 15, 11]) # 需要拟合的函数func :指定函数的形状,即n(t)的计算公式 def func(params, t): m, p, q = params fz = (p * (p + q) ** 2) * e ** (-(p + q) * t) # 分子的计算 fm = (p + q * e ** (-(p + q) * t)) ** 2 # 分母的计算 nt = m * fz / fm # nt值 return nt # 误差函数函数:x,y都是列表:这里的x,y更上面的Xi,Yi中是一一对应的 # 一般第一个参数是需要求的参数组,另外两个是x,y def error(params, t, y): return func(params, t) - y # k,b的初始值,可以任意设定, 一般需要根据具体场景确定一个初始值 p0 = [100, 0.3, 0.3] # 把error函数中除了p0以外的参数打包到args中(使用要求) params = leastsq(error, p0, args=(ti, yi)) params = params[0] # 读取结果 m, p, q = params print('m=', m) print('p=', p) print('q=', q) # 有了参数后,就是计算不同t情况下的拟合值 y_hat = [] for t in ti: y = func(params, t) y_hat.append(y) # 接下来我们绘制实际曲线和拟合曲线 # 由于模拟数据实在太好,两条曲线几乎重合了 fig = plt.figure() plt.scatter(ti, yi, color='r', label='true') plt.plot(ti, y_hat, color='b', label='predict') plt.title('BASS model') plt.legend()
以下是该程序的运行结果(我在jupyter notebook上运行的):