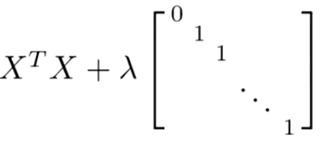过度拟合问题

• Underfitting (欠拟合）
• Overfitting (过拟合）
• 解决拟合的方法
• 线性回归正则化

欠拟合/高偏差（high bias）

过拟合/高方差（high variance）

过拟合与欠拟合也可以用 Bias 与 Variance 的角度来解释，欠拟合会导致高 Bias ，过拟合会导致高 Variance ，所以模型需要在 Bias 与 Variance 之间做出一个权衡。

特征过多但是训练集很小，就和容易出现过度拟合的问题。

过拟合的缺点就是不能够很好地泛化到新样本。

解决欠拟合的方法：

 

添加新的域特有特征和更多特征笛卡尔积，并更改特征处理所用的类型 (例如，增加 n 元大小)

减少使用的正则化数量

解决过拟合的方法：

特征选择：考虑使用更少的特征组合，减少 n 元大小。

模型选择算法

增加使用的正则化数量。

线性回归正则化

正则化项即罚函数，该项对模型向量进行“惩罚”，从而避免单纯最小二乘问题的过拟合问题。

对于线性回归(的求解)，我们之前运用了两种学习算法，一种基于梯度下降，一种基于正规方程。

1

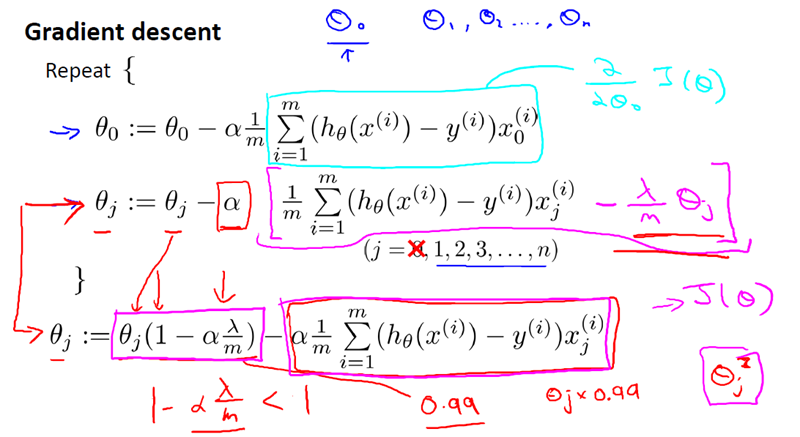
梯度下降，如下：

2

正规方程，如下：

3

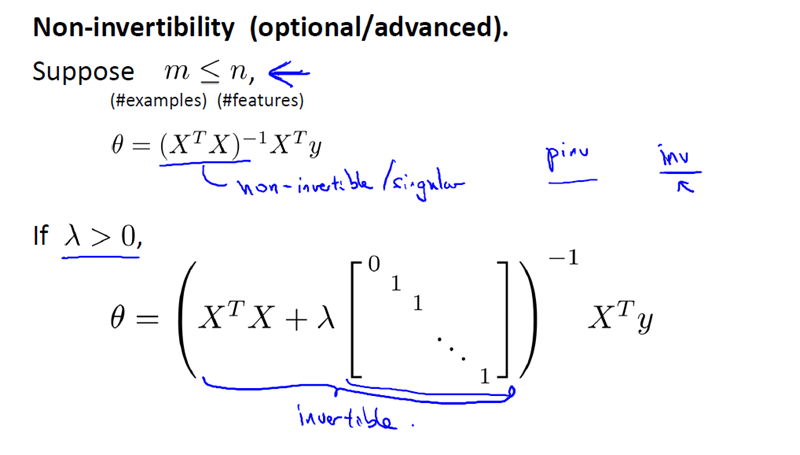
现在考虑 M（即样本量）， 比 N（即特征的数量）小或等于N。

当只有较少的样本，导致特征数量大于样本数量，那么矩阵 X^TX 将是不可逆矩阵或奇异（singluar）矩阵，或者用另一种说法是这个矩阵是退化（degenerate）的，那么我们就没有办法使用正规方程来求出 θ 。

幸运的是，正规化也为我们解决了这个问题，具体的说只要正则参数是严格大于零，实际上，可以证明如下矩阵：

将是可逆的。因此，使用正则还可以照顾任何 X^TX 不可逆的问题。

所以，你现在知道如何实现岭回归，利用它，你就可以避免过度拟合，即使你在一个相对较小的训练集里有很多特征。这应该可以让你在很多问题上更好的运用线性回归。

在接下来的视频中，我们将把这种正则化的想法应用到 Logistic 回归，这样我们就可以让 logistic 回归也避免过度拟合，从而表现的更好。

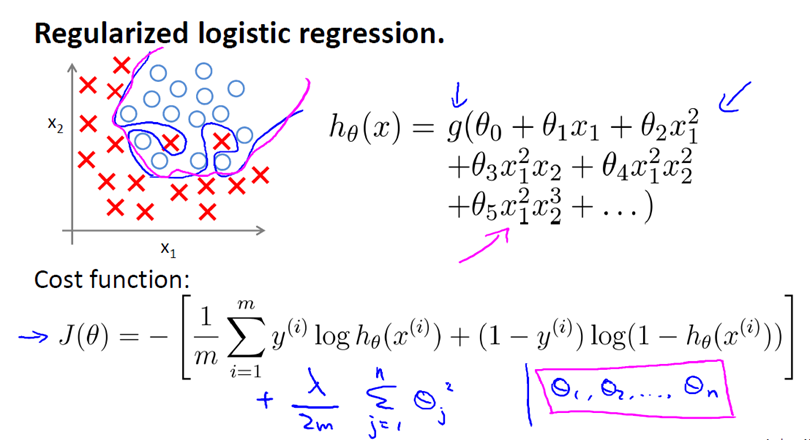
逻辑回归正则化

Regularized Logistic Regression 实际上与 Regularized Linear Regression 是十分相似的。

同样使用梯度下降：