主要内容:
一、感知机模型
二、感知机学习策略(线性可分)
三、感知机学习算法
(疑问:对偶形式比原始形式更优吗?但为何从”判断误分类点“这一步骤对比,对偶形式的时间复杂度似乎更高呢?)
一、感知机模型
1.所谓感知机,其实就是一个在n维空间内的超平面(n-1维),这个超平面将整个空间分为两部分。
2.该超平面S被定义为:w*x + b = 0。其中,w*x + b >= 0 的那部分空间被定义为正,w*x + b < 0 的那部分空间被定义为负,即:
![]()
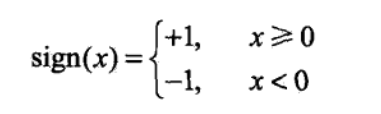
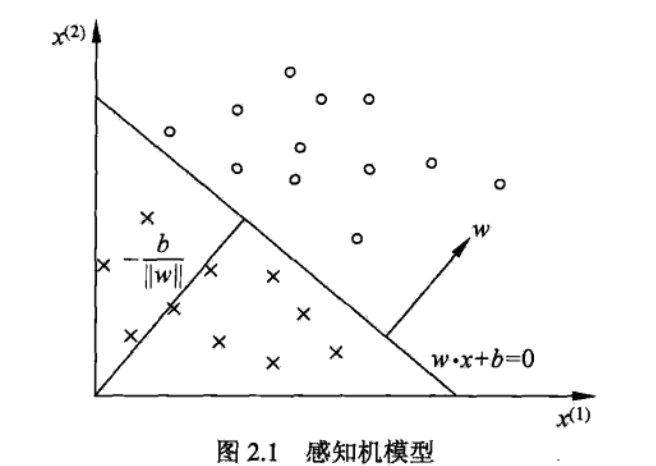
3.超平面S又称为分离超平面,如下图:
二、感知机学习策略(线性可分)
1. 对于一个线性可分的训练集,我们能够找到(至少)一个分离超平面,该超平面能把训练集的正、负实例点完全地分离开。为了找到该平面,需要确定一个学习策略,即定义经验损失函数。
2.感知机采用的损失函数是:误分类点到超平面的距离,即:![]() 。而又因为其是误分类点,yi与w*xi+b异号,即
。而又因为其是误分类点,yi与w*xi+b异号,即![]() ,所以误分类点到超平面的距离又为:
,所以误分类点到超平面的距离又为:![]() 。
。
3. 若超平面S的误分类点集合为M,则所有误分类点到超平面的总距离为:![]() ,如果如考虑1/||w||(对损失函数乘上一个非0常数并不会影响极值点的取值),那么就得到感知机的损失函数:
,如果如考虑1/||w||(对损失函数乘上一个非0常数并不会影响极值点的取值),那么就得到感知机的损失函数:
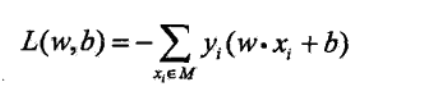
三、感知机学习算法
1. 感知机学习算法的原始形式:该算法使用的是梯度下降,但在极小化的过程中并非一次使得M中的误分类点的梯度下降,而是一次随机选取一个误分类点进行梯度下降。


2. 算法的收敛性:在训练集线性可分的时候,感知机学习算法的原始形式会收敛,而不可能一直迭代下去。即经过有限次迭代,可以得到一个将训练集完全正确划分的分离超平面及感知机模型。且有以下定理:

3.感知机学习算法的对偶性形式:


