HDU1560 DNA sequence —— IDA*算法

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=1560

DNA sequence

Time Limit: 15000/5000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 2999    Accepted Submission(s): 1462

Problem Description

The twenty-first century is a biology-technology developing century. We know that a gene is made of DNA. The nucleotide bases from which DNA is built are A(adenine), C(cytosine), G(guanine), and T(thymine). Finding the longest common subsequence between DNA/Protein sequences is one of the basic problems in modern computational molecular biology. But this problem is a little different. Given several DNA sequences, you are asked to make a shortest sequence from them so that each of the given sequence is the subsequence of it.

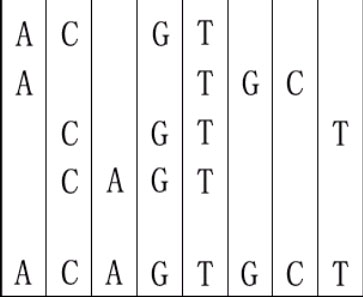
For example, given "ACGT","ATGC","CGTT" and "CAGT", you can make a sequence in the following way. It is the shortest but may be not the only one.

 

Input

The first line is the test case number t. Then t test cases follow. In each case, the first line is an integer n ( 1<=n<=8 ) represents number of the DNA sequences. The following k lines contain the k sequences, one per line. Assuming that the length of any sequence is between 1 and 5.

 

Output

For each test case, print a line containing the length of the shortest sequence that can be made from these sequences.

 

Sample Input

1 4 ACGT ATGC CGTT CAGT

 

Sample Output

8

 

Author

LL

 

Source

HDU 2006-12 Programming Contest

题解：

一开始以为是直接用回溯的方法，结果TLE。看了题解是用IDA*（迭代加深搜），其实自己不太了解迭代加深搜为什么比较快，而且什么时候用合适？下面是自己对迭代加深搜的一些浅薄的了解：

1.首先迭代加深搜适合用在：求最少步数（带有BFS的特点）并且不太容易估计搜索深度的问题上，同时兼有了BFS求最少步数和DFS易写、无需多开数组的特点。

2.相对于赤裸裸的回溯，迭代加深搜由于限制了搜索深度，所以也能适当地剪枝。

3.我编不下去了……

代码一：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <vector>
#include <queue>
#include <stack>
#include <map>
#include <string>
#include <set>
#define ms(a,b) memset((a),(b),sizeof((a)))
using namespace std;
typedef long long LL;
const int INF = 2e9;
const LL LNF = 9e18;
const int MOD = 1e9+7;
const int MAXN = 10+10;

int n;
char dna[MAXN][MAXN];
int len[MAXN], pos[MAXN];
char s[4] = {'A', 'G', 'C', 'T'};

bool dfs(int k, int limit)  //k为放了几个， k+1才为当前要放的
{
    int maxx = 0, cnt = 0;  //maxx为最长剩余的dna片段， cnt为剩余的片段之和（核苷酸链？好怀念啊）
    for(int i = 0; i<n; i++)
    {
        cnt += len[i]-pos[i];
        maxx = max(maxx, len[i]-pos[i]);
    }
    if(cnt==0) return true;    //如果片段都放完，则已得到答案
    if(cnt<=limit-k) return true;   //剪枝：片段之和小于等于剩余能放数量，肯定能够得到答案
    if(maxx>limit-k) return false;  //剪枝：最小的估计值都大于剩余能放数量，肯定不能得到答案

    int tmp[MAXN];
    for(int i = 0; i<4; i++)
    {
        memcpy(tmp, pos, sizeof(tmp));
        bool flag = false;
        for(int j = 0; j<n; j++)
            if(dna[j][pos[j]]==s[i])
                pos[j]++, flag = true;

        //k+1<=limit：在限制范围内
        if(k+1<=limit && flag && dfs(k+1, limit) )
            return true;
        memcpy(pos, tmp, sizeof(pos));
    }
    return false;
}

int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d",&n);
        int limit = 0;
        for(int i = 0; i<n; i++)
        {
            scanf("%s",dna[i]);
            len[i] = strlen(dna[i]);
            limit = max(limit, len[i]);
        }

        ms(pos, 0);
        while(!dfs(0, limit))
            limit++;
        printf("%d
", limit);
    }
}

代码二：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <vector>
#include <queue>
#include <stack>
#include <map>
#include <string>
#include <set>
#define ms(a,b) memset((a),(b),sizeof((a)))
using namespace std;
typedef long long LL;
const int INF = 2e9;
const LL LNF = 9e18;
const int MOD = 1e9+7;
const int MAXN = 10+10;

int n;
char dna[MAXN][MAXN];
int len[MAXN], pos[MAXN];
char s[4] = {'A', 'G', 'C', 'T'};

bool dfs(int k, int limit)  //k为放了几个， k+1才为当前要放的
{
    if(k>limit) return false;

    int maxx = 0, cnt = 0;  //maxx为最长剩余的dna片段， cnt为剩余的片段之和（核苷酸链？好怀念啊）
    for(int i = 0; i<n; i++)
    {
        cnt += len[i]-pos[i];
        maxx = max(maxx, len[i]-pos[i]);
    }
    if(cnt==0) return true;    //如果片段都放完，则已得到答案
    if(cnt<=limit-k) return true;   //剪枝：片段之和小于等于剩余能放数量，肯定能够得到答案
    if(maxx>limit-k) return false;  //剪枝：最小的估计值都大于剩余能放数量，肯定不能得到答案

    int tmp[MAXN];
    for(int i = 0; i<4; i++)
    {
        memcpy(tmp, pos, sizeof(tmp));
        bool flag = false;
        for(int j = 0; j<n; j++)
            if(dna[j][pos[j]]==s[i])
                pos[j]++, flag = true;

        if(flag && dfs(k+1, limit) )
            return true;
        memcpy(pos, tmp, sizeof(pos));
    }
    return false;
}

int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d",&n);
        int limit = 0;
        for(int i = 0; i<n; i++)
        {
            scanf("%s",dna[i]);
            len[i] = strlen(dna[i]);
            limit = max(limit, len[i]);
        }

        ms(pos, 0);
        while(!dfs(0, limit))
            limit++;
        printf("%d
", limit);
    }
}