Uvalive 4043 Ants —— 二分图最大权匹配 KM算法

题目链接：https://vjudge.net/problem/UVALive-4043

题意：

给出n个白点和n个黑点的坐标， 要求用n条不相交的线段把他们连接起来，其中每条线段恰好连接一个白点和黑点，每个点恰好连接到一条线段。输出每个白点与其相连的黑点的编号。

题解：

1.首先随便配对。然后，如果存在两对黑白点的线段是相交的，那么就交换他们的配对对象。交换之后重新形成的线段就不会相交了（画画图就可看出）。而且可以推出一个结论：交换之后，两条线段之和必定变小。这是因为根据三角形定理：

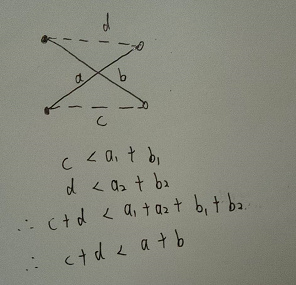
2.有了上述结论之后，我们就能推出：对于当前配对，如果线段总和还能继续变小，那么就可能存在交叉；但如果线段总和不能再小了，即已经达到最小，那么就不存在交叉了。所以我们只需要求最大权匹配（边权取反），就能满足要求了。

代码如下：

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int INF = 2e9;
const LL LNF = 9e18;
const double EPS = 1e-8;
const int MOD = 1e9+7;
const int MAXN = 1e2+10;

struct Node{
    double x, y;
}black[MAXN], white[MAXN];

int nx, ny;
double  g[MAXN][MAXN];
int linker[MAXN];
double lx[MAXN], ly[MAXN], slack[MAXN];
bool visx[MAXN], visy[MAXN];

bool DFS(int x)
{
    visx[x] = true;
    for(int y = 1; y<=ny; y++)
    {
        if(visy[y]) continue;
        double tmp = lx[x] + ly[y] - g[x][y];
        if(tmp<EPS)
        {
            visy[y] = true;
            if(linker[y]==-1 || DFS(linker[y]))
            {
                linker[y] = x;
                return true;
            }
        }
        else
            slack[y] = min(slack[y], tmp);
    }
    return false;
}

void KM()
{
    memset(linker, -1, sizeof(linker));
    memset(ly, 0, sizeof(ly));
    for(int i = 1; i<=nx; i++)
    {
        lx[i] = -INF;
        for(int j = 1; j<=ny; j++)
            lx[i] = max(lx[i], g[i][j]);
    }

    for(int x = 1; x<=nx; x++)
    {
        for(int i = 1; i<=ny; i++)
            slack[i] = INF;
        while(true)
        {
            memset(visx, 0, sizeof(visx));
            memset(visy, 0, sizeof(visy));

            if(DFS(x)) break;
            double d = INF;
            for(int i = 1; i<=ny; i++)
                if(!visy[i])
                    d = min(d, slack[i]);

            for(int i = 1; i<=nx; i++)
                if(visx[i])
                    lx[i] -= d;
            for(int i = 1; i<=ny; i++)
            {
                if(visy[i]) ly[i] += d;
                else slack[i] -= d;
            }
        }
    }
}

int main()
{
    int kase = 0, n;
    while(scanf("%d", &n) != EOF)
    {
        if(kase++) printf("
");

        nx = ny = n;
        for (int i = 1; i <= n; i++)
            scanf("%lf%lf", &black[i].x, &black[i].y);
        for (int i = 1; i <= n; i++)
            scanf("%lf%lf", &white[i].x, &white[i].y);

        for (int i = 1; i <= n; i++)
        {
            double x1 = white[i].x, y1 = white[i].y;
            for (int j = 1; j <= n; j++)
            {
                double x2 = black[j].x, y2 = black[j].y;
                g[i][j] = -sqrt( (x1-x2)*(x1 - x2) + (y1-y2)*(y1-y2) );
            }
        }

        KM();
        for(int i = 1; i<=n; i++)
            printf("%d
", linker[i]);
    }
}