HDU4990 Reading comprehension —— 递推、矩阵快速幂

题目链接：https://vjudge.net/problem/HDU-4990

Reading comprehension

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 2329    Accepted Submission(s): 954

Problem Description

Read the program below carefully then answer the question.
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include <cstdio>
#include<iostream>
#include <cstring>
#include <cmath>
#include <algorithm>
#include<vector>

const int MAX=100000*2;
const int INF=1e9;

int main()
{
  int n,m,ans,i;
  while(scanf("%d%d",&n,&m)!=EOF)
  {
    ans=0;
    for(i=1;i<=n;i++)
    {
      if(i&1)ans=(ans*2+1)%m;
      else ans=ans*2%m;
    }
    printf("%d ",ans);
  }
  return 0;
}

 

Input

Multi test cases，each line will contain two integers n and m. Process to end of file.
[Technical Specification]
1<=n, m <= 1000000000

 

Output

For each case，output an integer，represents the output of above program.

 

Sample Input

1 10 3 100

 

Sample Output

1 5

 

Source

BestCoder Round #8

 

Recommend

heyang

题解：

当n为奇数时，f[n] = 2*f[n-1]+1，f[n-1] = 2*f[n-2]，所以：f[n] = f[n-1] + 2*f[n-2] + 1;

当n为偶数时，f[n] = 2*f[n-1]，f[n-1] = 2*f[n-2] + 1，所以：f[n] = f[n-1] + 2*f[n-2] + 1;

综上：f[n] = f[n-1] + 2*f[n-2] + 1，构造矩阵：

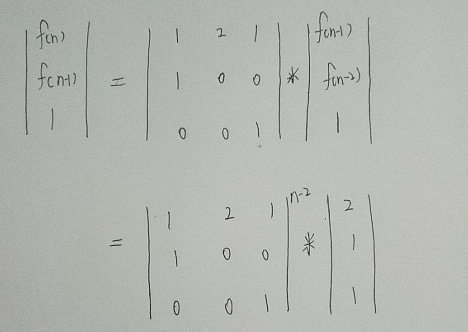
代码如下：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>
#include <cmath>
#include <queue>
#include <stack>
#include <map>
#include <string>
#include <set>
using namespace std;
typedef long long LL;
const int INF = 2e9;
const LL LNF = 9e18;
//const int MOD = 10000007;
const int MAXN = 1e6+100;

LL MOD;
const int Size = 3;
struct MA
{
    LL mat[Size][Size];
    void init()
    {
        for(int i = 0; i<Size; i++)
        for(int j = 0; j<Size; j++)
            mat[i][j] = (i==j);
    }
};

MA mul(MA x, MA y)
{
    MA ret;
    memset(ret.mat, 0, sizeof(ret.mat));
    for(int i = 0; i<Size; i++)
    for(int j = 0; j<Size; j++)
    for(int k = 0; k<Size; k++)
        ret.mat[i][j] += (1LL*x.mat[i][k]*y.mat[k][j])%MOD, ret.mat[i][j] %= MOD;
    return ret;
}

MA qpow(MA x, LL y)
{
    MA s;
    s.init();
    while(y)
    {
        if(y&1) s = mul(s, x);
        x = mul(x, x);
        y >>= 1;
    }
    return s;
}

MA tmp = {
    1, 2, 1,
    1, 0, 0,
    0, 0, 1
};

int main()
{
    LL n, m;
    while(scanf("%lld%lld",&n,&m)!=EOF)
    {
        MOD = m;
        if(n<=2)
        {
            printf("%lld
", n%MOD);
            continue;
        }

        MA s = tmp;
        s = qpow(s, n-2);

        LL ans = ((2LL*s.mat[0][0]%MOD + s.mat[0][1])%MOD+s.mat[0][2])%MOD;
        printf("%lld
", ans);
    }
}