主要内容:
一.模型介绍
二.算法过程
三.算法性能评估及ε(threshold)的选择
四.Anomaly detection vs Supervised learning
五.Multivariate Gaussian
一.模型介绍
如何检测一个成品是否异常?
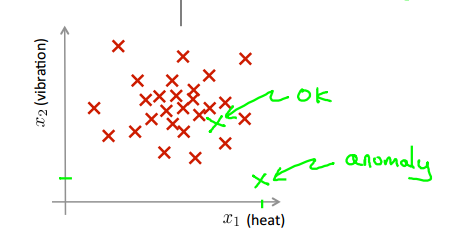
假设红交叉表示正常的样本点,如果抽取到的成品其位于正常样本点的范围之内,则可认为其正常;如果成品的位置远离正常样本点,则可认为其出现异常。
为了更加明确“正常样本点”的范围,我们添加圈圈以划定区域,如:
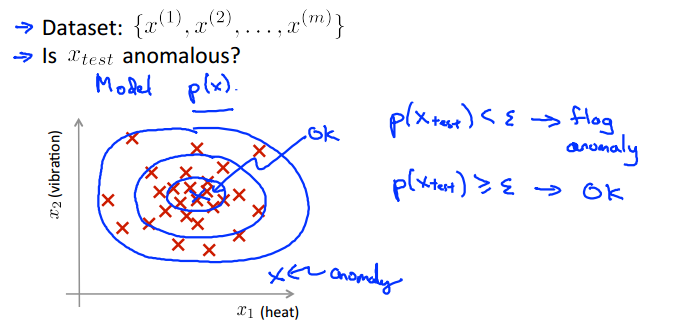
此时,选择一个threshold,即ε,以划定正常与异常的边界。
当p(Xtest) >= ε,可认为是正常;
当p(Xtest) < ε,可认为是异常。
而这个p()就是高斯分布函数,即正态分布函数。
二.算法过程

注意,此限制是:所有特征都必须相互独立,才满足公式:P(AB) = P(a)*P(B)。
三.算法性能评估及ε(threshold)的选择


四.Anomaly detection vs Supervised learning
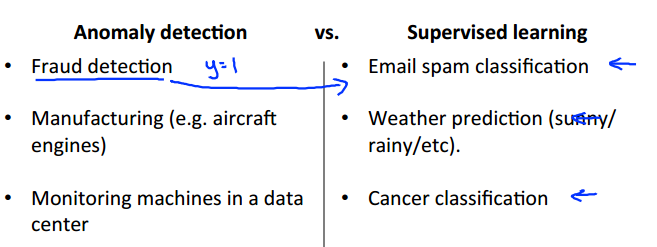
貌似利用高斯分布函数来检测异常的方法跟Logistic回归进行二分类的方法十分相似。确实如此,但两者有不同的使用场合:

五.Multivariate Gaussian
之前使用的高斯分布函数都要求各个特征相互独立,而现实往往并非如此。因此需要使用Multivariate Gaussian(不知道中文应该怎么叫,就先叫做多维正态分布吧),它适用于特征不独立的条件。
而讲到多维正态分布,就离不开讲协方差矩阵。
1) 当各个特征相互独立时,其协方差矩阵为对角矩阵,其中对角线元素即为其每个特征的方差。而分布图其实“随坐标轴”的。

2) 当各个特征不相互独立时,其协方差矩阵就不是对角矩阵了。而其分布图是“不随坐标轴”的。
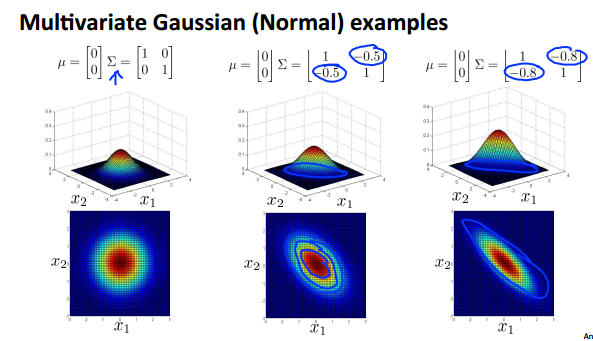
有关协方差的含义,可看此博客:终于明白协方差的意义了
了解多维正态分布后,就可以用它来改进检测方法了:

虽然改进后的多维正态分布适用性更强了,但却不一定处处体现出优势。因此以下列出了原始模型与改进模型的使用条件:
