主要内容:
一.算法概述
二.距离度量
三.k值的选择
四.分类决策规则
五.利用KNN对约会对象进行分类
六.利用KNN构建手写识别系统
七.KNN之线性扫描法的不足
八.KD树
一.算法概述
1.k近邻算法,简而言之,就是选取k个与输入点的特征距离最近的数据点中出现最多的一种分类,作为输入点的类别。
2.如下面一个例子,有六部电影,可用“打斗镜头”和“接吻镜头”作为每一部电影的特征值,且已知每一部电影的类别,即“爱情片”还是“动作片”。此外,还有一部电影,只知道其特征,但不知道其类别。如下:

为了方便研究,可以将其放到二维平面上:

为了得出?的类别,可以选择与之距离最近的k部电影,然后将这k部电影中出现次数最多的类别作为该部电影的类别。
?与每一部电影的距离为:
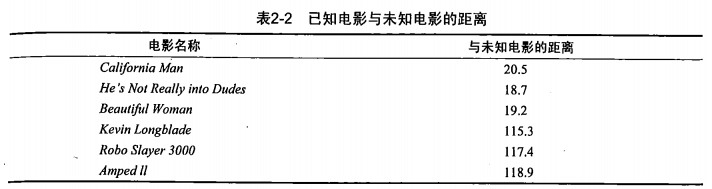
假如选取k为3,而前面3部电影的类别均为爱情片,所以可以认为?的类别为爱情片。
3.通过例子可以看出,KNN算法的三个基本要素为:距离度量、k值的选择、分类决策规则,下面将一一讲解。
二.距离度量
1.特征空间中两个实例点的距离反应了两个实例点的相似程度,k近邻模型的特征空间是n维的实数向量空间。其中使用的距离是欧式距离,即我们平常所说的“直线距离”,但也可以是其他距离。或者可以归于一个类别,即Lp距离。其基本介绍如下:
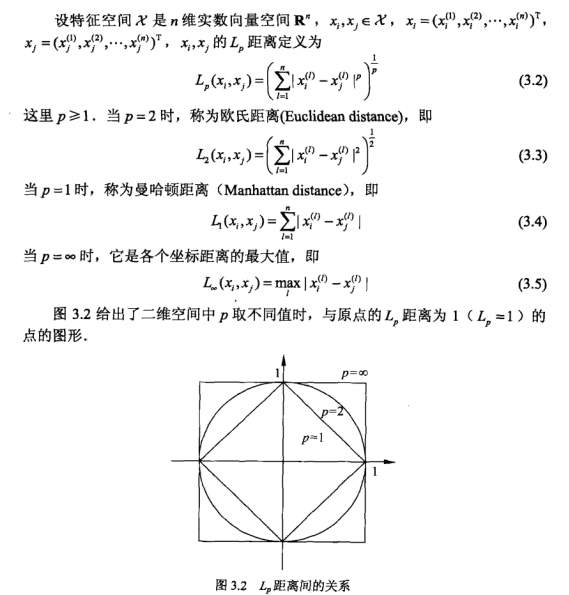
三.k值的选择
从直觉上可得出:k值的选择对模型的有效性影响很大。
1.如果k值选得比较小,那么预测结果会对临近的点十分敏感。假如附近的点刚好是噪声,那么预测结果就会出错。总体而言,容易发生过拟合。
2.假如k值选得比较大,那么预测结果就很容易受到数量大的类别的干扰,特别地,当k=N时,那么类别就永远为数量最大的那个类别,算法就没有意义的。
3.综上,k过大或者过小,预测结果都可能变得糟糕。所以可以通过交叉验证法来选取最优值k。
思考:在选取了k个最近点之后,每个点对于预测结果的影响所占的权值都是一样的,即都是“一票”,但可不可以设置权值:越靠近的点权值越大呢?这样做会不会好一点?不过这个问题好像归类于下面一节的。
四.分类决策规则
分类决策规则,即得到k个最近点之后,通过什么方式去决定最终的分类。从直觉上可感觉到选取数量最多的那个类别作为输入点的类别或许是比较合理的。下面是具体的数学解释:

五.利用KNN对约会对象进行分类
海伦最近在约会网站上寻找适合自己的约会对象。经过一番总结,她将约会对象分为三种类别:
...不喜欢的人
...魅力一般的人
...极具魅力的人
此外,每个约会对象还有三种特征,分别是:
...每年获得的飞行常客里程数
...玩视频游戏所消耗时间百分比
...每周消费的冰淇淋公升数
为了帮助海伦预测她没有约会过的对象属于那种类别,我们需要根据已有的数据(即已经约会过的对象),利用KNN算法来构建一个预测系统。
基本流程如下:

Python代码:

1 # coding:utf-8
2 from numpy import *
3 import operator
4 from os import listdir
5
6 def file2matrix(filename): #从文件中提取数据
7 fr = open(filename)
8 numberOfLines = len(fr.readlines()) #数据的条数
9 returnMat = zeros((numberOfLines,3)) #特征数组X
10 classLabelVector = [] #每条数据对应的分类Y
11 fr = open(filename)
12 index = 0
13 for line in fr.readlines(): #读取每一条数据
14 line = line.strip()
15 listFromLine = line.split(' ')
16 returnMat[index,:] = listFromLine[0:3] #读取特征x
17 classLabelVector.append(int(listFromLine[-1])) #读取分类y
18 index += 1
19 return returnMat,classLabelVector #返回特征数组X和分类数组Y
20
21 def autoNorm(dataSet): #特征归一化,作用是:使得每个特征的权重相等。范围[0,1]
22 minVals = dataSet.min(0)
23 maxVals = dataSet.max(0)
24 ranges = maxVals - minVals
25 normDataSet = zeros(shape(dataSet))
26 m = dataSet.shape[0]
27 normDataSet = dataSet - tile(minVals, (m,1))
28 normDataSet = normDataSet/tile(ranges, (m,1))
29 return normDataSet, ranges, minVals #返回归一化矩阵、范围、最小值
30
31
32 def classify0(inX, dataSet, labels, k): #使用KNN进行分类
33 dataSetSize = dataSet.shape[0] #训练数据集的大小
34 diffMat = tile(inX, (dataSetSize,1)) - dataSet #从此步起到第四步为计算欧氏距离
35 sqDiffMat = diffMat**2
36 sqDistances = sqDiffMat.sum(axis=1)
37 distances = sqDistances**0.5
38 sortedDistIndicies = distances.argsort() #对距离进行排序,得到的是排序后的下标,而不是数据本身
39 classCount={} #记录k近邻中每种类别出现的次数
40 for i in range(k): #枚举k近邻
41 voteIlabel = labels[sortedDistIndicies[i]] #获取该数据点的类别
42 classCount[voteIlabel] = classCount.get(voteIlabel,0) + 1 #累加
43 sortedClassCount = sorted(classCount.iteritems(), key=operator.itemgetter(1), reverse=True) #排序
44 return sortedClassCount[0][0] #返回数量最多的类别
45
46 def datingClassTest(): #使用KNN对约会对象进行分类的测试
47 hoRatio = 0.50 #用于测试的数据所占的比例
48 datingDataMat,datingLabels = file2matrix('datingTestSet2.txt') #读取数据
49 normMat, ranges, minVals = autoNorm(datingDataMat) #特征归一化
50 m = normMat.shape[0] #数据总量:训练数据+测试数据
51 numTestVecs = int(m*hoRatio) #训练数据的总量
52 errorCount = 0.0 #分类错误的总数
53 for i in range(numTestVecs): #利用KNN为每个测试数据进行分类
54 classifierResult = classify0(normMat[i,:],normMat[numTestVecs:m,:],datingLabels[numTestVecs:m],3) #得到分类结果
55 print "the classifier came back with: %d, the real answer is: %d" % (classifierResult, datingLabels[i]) #输出结果
56 if (classifierResult != datingLabels[i]): errorCount += 1.0 #如果分类错误,则累计
57 print "the total error rate is: %f" % (errorCount/float(numTestVecs)) #最后计算错误率
58 print "the total error count is: %d"%errorCount
59
60 if __name__ == "__main__":
61 datingClassTest()
运行结果如下:

错误率为6.4%,效果还是挺好的。
六.利用KNN构建手写识别系统
KNN算法还可用于识别手写字。为了方便,这里构造的识别系统自能识别0~9的的数字。
首先,我们可以将手写字投影到一个矩阵中,有墨水的地方就设为1,空白的地方设为0,如图:
 (分别是:9 2 7)
(分别是:9 2 7)
这是一个32*32的矩阵,我们将其转换为1*1024的一维向量以方便操作。之后,就可以利用KNN进行识别了,这里选取的k为3。
Python代码:

1 # coding:utf-8
2 from numpy import *
3 import operator
4 from os import listdir
5
6 def file2matrix(filename): # 从文件中提取数据
7 fr = open(filename)
8 numberOfLines = len(fr.readlines()) # 数据的条数
9 returnMat = zeros((numberOfLines, 3)) # 特征数组X
10 classLabelVector = [] # 每条数据对应的分类Y
11 fr = open(filename)
12 index = 0
13 for line in fr.readlines(): # 读取每一条数据
14 line = line.strip()
15 listFromLine = line.split(' ')
16 returnMat[index, :] = listFromLine[0:3] # 读取特征x
17 classLabelVector.append(int(listFromLine[-1])) # 读取分类y
18 index += 1
19 return returnMat, classLabelVector # 返回特征数组X和分类数组Y
20
21 def classify0(inX, dataSet, labels, k): # 使用KNN进行分类
22 dataSetSize = dataSet.shape[0] # 训练数据集的大小
23 diffMat = tile(inX, (dataSetSize, 1)) - dataSet # 从此步起到第四步为计算欧氏距离
24 sqDiffMat = diffMat ** 2
25 sqDistances = sqDiffMat.sum(axis=1)
26 distances = sqDistances ** 0.5
27 sortedDistIndicies = distances.argsort() # 对距离进行排序,得到的是排序后的下标,而不是数据本身
28 classCount = {} # 记录k近邻中每种类别出现的次数
29 for i in range(k): # 枚举k近邻
30 voteIlabel = labels[sortedDistIndicies[i]] # 获取该数据点的类别
31 classCount[voteIlabel] = classCount.get(voteIlabel, 0) + 1 # 累加
32 sortedClassCount = sorted(classCount.iteritems(), key=operator.itemgetter(1), reverse=True) # 排序
33 return sortedClassCount[0][0] # 返回数量最多的类别
34
35 def img2vector(filename): # 将32*32的二维数组转换成1*1024的一维数组
36 returnVect = zeros((1, 1024))
37 fr = open(filename)
38 for i in range(32):
39 lineStr = fr.readline()
40 for j in range(32):
41 returnVect[0, 32 * i + j] = int(lineStr[j])
42 return returnVect
43
44 def handwritingClassTest():
45 hwLabels = []
46 trainingFileList = listdir('trainingDigits') # 读取训练数据
47 m = len(trainingFileList) # m为数据的条数
48 trainingMat = zeros((m, 1024)) # 特征矩阵X
49 for i in range(m):
50 fileNameStr = trainingFileList[i]
51 fileStr = fileNameStr.split('.')[0]
52 classNumStr = int(fileStr.split('_')[0])
53 hwLabels.append(classNumStr) # 读取类别y
54 trainingMat[i, :] = img2vector('trainingDigits/%s' % fileNameStr) # 读取特征x
55 testFileList = listdir('testDigits') # 读取测试数据
56 errorCount = 0.0
57 mTest = len(testFileList)
58 for i in range(mTest):
59 fileNameStr = testFileList[i]
60 fileStr = fileNameStr.split('.')[0]
61 classNumStr = int(fileStr.split('_')[0])
62 vectorUnderTest = img2vector('testDigits/%s' % fileNameStr) # 读取特征x
63 classifierResult = classify0(vectorUnderTest, trainingMat, hwLabels, 3) # 利用KNN进行分类
64 print "the classifier came back with: %d, the real answer is: %d" % (classifierResult, classNumStr)
65 if (classifierResult != classNumStr): errorCount += 1.0 # 如果分类错误,则累加
66 print "
the total number of errors is: %d" % errorCount
67 print "
the total error rate is: %f" % (errorCount / float(mTest)) # 最后输出错误率
68
69 if __name__ == "__main__":
70 handwritingClassTest()
运行结果如下:

七.KNN之线性扫描法的不足
KNN最简单的实现方法就是线性扫描。但是,该做法需要求出输入点与每个训练点的距离,且还需要进行排序、统计。假如训练集很大,且特征的维度很高,那么计算量将会变得十分庞大,这时,线性扫描法将不可行。为了提高k近邻的搜索效率,可以使用特殊的数据结构来存储训练集,以减少计算距离的次数,于是就引入了KD树。下一篇博客进行详细介绍。
八.KD树
1.KD树的构造


例子:
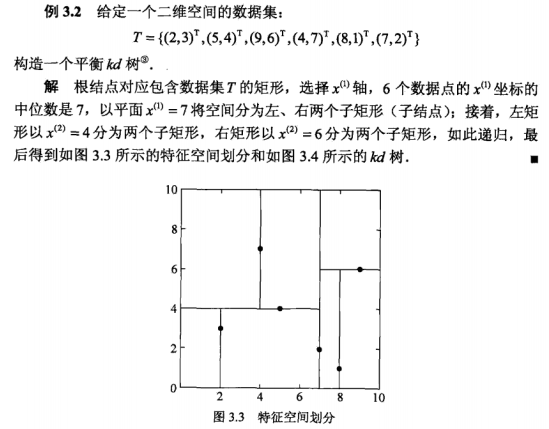
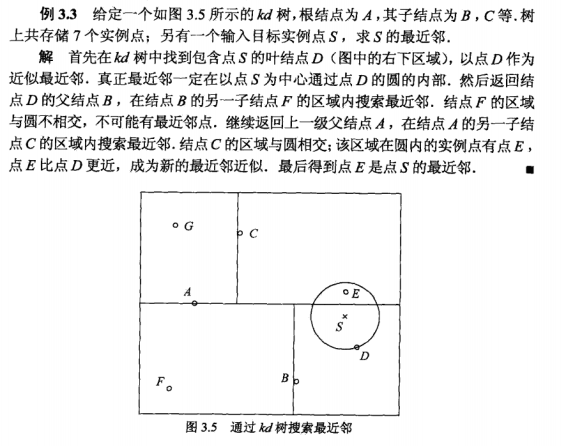
2.搜索KD树


例子:
3.KD树Python代码实现(来自《机器学习—K近邻,KD树算法python实现》)
代码:

1 # -*- coding: utf-8 -*- 2 """ 3 Created on Thu Dec 14 17:46:52 2017 4 5 @author: Q 6 """ 7 import numpy as np 8 import matplotlib.pyplot as plt 9 10 def createKDTree(dataSet,depth): #构造kd树 11 n = np.shape(dataSet)[0] 12 if n == 0: #列表为空,则返回空值 13 return None 14 15 treeNode = {} #当前节点 16 n, m = np.shape(dataSet) #n为实例点的个数,m为维度 17 split_axis = depth % m #轮流选取特征,作为空间切割的依据 18 treeNode['split'] = split_axis #记录切割空间的特征 19 dataSet = sorted(dataSet, key=lambda a: a[split_axis]) #在选取特征数对实例点进行排序 20 num = n // 2 21 treeNode['median'] = dataSet[num] #选取特征是中位数的实例点作为该节点 22 treeNode['left'] = createKDTree(dataSet[:num], depth + 1) #递归左右子树继续进行切割空间、构造kd树 23 treeNode['right'] = createKDTree(dataSet[num + 1:], depth + 1) 24 return treeNode 25 26 27 def searchTree(tree,point): #在KD树中搜索point的最近邻 28 k = len(point) #k为维度 29 if tree is None: #如果当前节点为空,则直接返回“距离无限大”表示不可能 30 return [0]*k, float('inf') 31 32 '''在切割特征上,根据大小进入相应的子树''' 33 split_axis = tree['split'] #获取切割特征 34 median_point = tree['median'] #获取该节点的实例点 35 if point[split_axis] <= median_point[split_axis]: #在切割特征上,根据大小进入相应的子树 36 nearestPoint,nearestDistance = searchTree(tree['left'],point) 37 else: 38 nearestPoint,nearestDistance = searchTree(tree['right'],point) 39 nowDistance = np.linalg.norm(point-median_point) #计算point与当前实例点的距离 40 if nowDistance < nearestDistance: #如果两者距离小于最近距离,则更新 41 nearestDistance = nowDistance 42 nearestPoint = median_point.copy() 43 44 '''检测最近点是否可能出现在另外一颗子树所表示的超平面''' 45 splitDistance = abs(point[split_axis] - median_point[split_axis]) #计算point与另一个子树所表示的超平面的距离 46 if splitDistance > nearestDistance: #如果两者距离小于当前的最近距离,则最近点必定不可能落在另一棵子树所表示的平面上,直接返回 47 return nearestPoint,nearestDistance 48 else: #否则,最近点有可能落在另一棵子树所表示的平面上,继续搜索 49 if point[split_axis] <= median_point[split_axis]: 50 nextTree = tree['right'] 51 else: 52 nextTree = tree['left'] 53 nearPoint,nearDistanc = searchTree(nextTree,point) #进入另一棵子树继续搜索 54 if nearDistanc < nearestDistance: #更新 55 nearestDistance = nearDistanc 56 nearestPoint = nearPoint.copy() 57 return nearestPoint,nearestDistance #返回当前结果 58 59 60 def loadData(fileName): 61 dataSet = [] 62 with open(fileName) as fd: 63 for line in fd.readlines(): 64 data = line.strip().split() 65 data = [float(item) for item in data] 66 dataSet.append(data) 67 dataSet = np.array(dataSet) 68 label = dataSet[:,2] 69 dataSet = dataSet[:,:2] 70 return dataSet,label 71 72 73 if __name__ == "__main__": 74 '''加载数据,并绘制离散图''' 75 dataSet,label = loadData('testSet.txt') 76 fig = plt.figure() 77 ax = fig.add_subplot(1,1,1) 78 ax.scatter(dataSet[:,0],dataSet[:,1],c = label,cmap = plt.cm.Paired) 79 '''构造KD树''' 80 tree = createKDTree(dataSet, 0) 81 '''搜索最近邻''' 82 point = [3,9.8] 83 nearpoint,neardis = searchTree(tree,point) 84 '''将结果标示于离散图上''' 85 ax.scatter(point[0],point[1],c = 'g',s=50) 86 ax.scatter(nearpoint[0],nearpoint[1],c = 'r',s=50) 87 plt.show()
训练数据:

-0.017612 14.053064 0 -1.395634 4.662541 1 -0.752157 6.538620 0 -1.322371 7.152853 0 0.423363 11.054677 0 0.406704 7.067335 1 0.667394 12.741452 0 -2.460150 6.866805 1 0.569411 9.548755 0 -0.026632 10.427743 0 0.850433 6.920334 1 1.347183 13.175500 0 1.176813 3.167020 1 -1.781871 9.097953 0 -0.566606 5.749003 1 0.931635 1.589505 1 -0.024205 6.151823 1 -0.036453 2.690988 1 -0.196949 0.444165 1 1.014459 5.754399 1 1.985298 3.230619 1 -1.693453 -0.557540 1 -0.576525 11.778922 0 -0.346811 -1.678730 1 -2.124484 2.672471 1 1.217916 9.597015 0 -0.733928 9.098687 0 -3.642001 -1.618087 1 0.315985 3.523953 1 1.416614 9.619232 0 -0.386323 3.989286 1 0.556921 8.294984 1 1.224863 11.587360 0 -1.347803 -2.406051 1 1.196604 4.951851 1 0.275221 9.543647 0 0.470575 9.332488 0 -1.889567 9.542662 0 -1.527893 12.150579 0 -1.185247 11.309318 0 -0.445678 3.297303 1 1.042222 6.105155 1 -0.618787 10.320986 0 1.152083 0.548467 1 0.828534 2.676045 1 -1.237728 10.549033 0 -0.683565 -2.166125 1 0.229456 5.921938 1 -0.959885 11.555336 0 0.492911 10.993324 0 0.184992 8.721488 0 -0.355715 10.325976 0 -0.397822 8.058397 0 0.824839 13.730343 0 1.507278 5.027866 1 0.099671 6.835839 1 -0.344008 10.717485 0 1.785928 7.718645 1 -0.918801 11.560217 0 -0.364009 4.747300 1 -0.841722 4.119083 1 0.490426 1.960539 1 -0.007194 9.075792 0 0.356107 12.447863 0 0.342578 12.281162 0 -0.810823 -1.466018 1 2.530777 6.476801 1 1.296683 11.607559 0 0.475487 12.040035 0 -0.783277 11.009725 0 0.074798 11.023650 0 -1.337472 0.468339 1 -0.102781 13.763651 0 -0.147324 2.874846 1 0.518389 9.887035 0 1.015399 7.571882 0 -1.658086 -0.027255 1 1.319944 2.171228 1 2.056216 5.019981 1 -0.851633 4.375691 1 -1.510047 6.061992 0 -1.076637 -3.181888 1 1.821096 10.283990 0 3.010150 8.401766 1 -1.099458 1.688274 1 -0.834872 -1.733869 1 -0.846637 3.849075 1 1.400102 12.628781 0 1.752842 5.468166 1 0.078557 0.059736 1 0.089392 -0.715300 1 1.825662 12.693808 0 0.197445 9.744638 0 0.126117 0.922311 1 -0.679797 1.220530 1 0.677983 2.556666 1 0.761349 10.693862 0 -2.168791 0.143632 1 1.388610 9.341997 0 0.317029 14.739025 0
