主要内容:
一. FP-growth算法简介
二.构建FP树
三.从一颗FP树中挖掘频繁项集
一. FP-growth算法简介
1.上次提到可以用Apriori算法来提取频繁项集,但是Apriori算法有个致命的缺点,那就是它对每个潜在的频繁项集都需要扫描数据集判定其是否频繁,因而在时间消耗上是巨大的。据说在实际应用上一般都不用Apriori算法,那用什么呢?FP-growth算法。
2.FP算法的核心就是将数据集存储在一个特定的称作FP树的结构当中,FP树与Trie树(字典树)十分相似,一样是共用“前缀”。构建完FP树之后,就可以递归地在FP树上挖掘频繁项集。FP-growth算法只需要对数据集进行两次扫描(第一次扫描在建树时,第二次扫描在哪里?惭愧,真看不出在哪里。),且利用到了类似Trie树这种节省“空间”的结构,运行起来比Apriori算法快了不少。
二.构建FP树
1.算法描述:
1)假设有六条数据,如下

2)为了将这些数据插进类似Trie树的结构中,且为了树的规模尽可能小(这样树的表示效率才高),可以想到:将集合型的数据通过按照字母出现频率降序排序,形成列表型的数据。因为将经常出现的字母都放在了每条数据的前面,在插入FP树中,公共前缀就更多了,即公共节点多了,树的规模就小了,所以树的表示效率就是高效的。

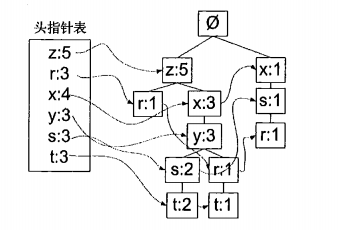
3)将每条数据重新调整后,就将数据插入到FP树中,其过程与Trie树无异。在建树的同时,还需要维护一个字母表,字母表需要记录字母的出现次数以及在FP树中出现的位置(位置通过链表维护)。
2.代码注释:
1 class treeNode: #树结点 2 def __init__(self, nameValue, numOccur, parentNode): 3 self.name = nameValue #这个结点所存的字母 4 self.count = numOccur #结点计数器 5 self.nodeLink = None #指向下一个同字母的结点的指针 6 self.parent = parentNode # 指向父节点的指针,用于上溯 7 self.children = {} #儿子结点的指针集 8 9 def inc(self, numOccur): #更新结点计数器 10 self.count += numOccur 11 12 def createTree(dataSet, minSup=1): #根据数据创建FP树,minSup为出现次数的阈值 13 headerTable = {} #字母表,需要存储两个信息:1.该字母的出现次数,2.指向该字母出现在FP树上的头指针 14 # 统计每个字母出现的次数 15 for trans in dataSet: #枚举每一条数据 16 for item in trans: #枚举该条数据的每一个字母 17 headerTable[item] = headerTable.get(item, 0) + dataSet[trans] #累加 18 for k in headerTable.keys(): # 枚举每一个字母,去除掉那些出现次数低于阈值的字母 19 if headerTable[k] < minSup: 20 del (headerTable[k]) 21 freqItemSet = set(headerTable.keys()) #将符合条件的字母放到一个set中,即freqItemSet 22 if len(freqItemSet) == 0: return None, None # if no items meet min support -->get out 23 for k in headerTable: #为headerTable开辟多一个位置,存放头指针 24 headerTable[k] = [headerTable[k], None] # reformat headerTable to use Node link 25 26 retTree = treeNode('Null Set', 1, None) # 创建根节点 27 for tranSet, count in dataSet.items(): # 将每一条数据插进FP树中,期间需要去除掉数据中出现次数低于阈值的字母,且数据中字母需要按出现次数进行降序排序 28 localD = {} #用于存放该数据中符合条件的字母 29 for item in tranSet: # 枚举这条数据的每个字母 30 if item in freqItemSet: #如果该字母符合条件,则放进localD中 31 localD[item] = headerTable[item][0] 32 if len(localD) > 0: 33 orderedItems = [v[0] for v in sorted(localD.items(), key=lambda p: p[1], reverse=True)] #将符合条件的字母按出现次数进行降序排序 34 updateTree(orderedItems, retTree, headerTable, count) # 然后将其插入FP树中 35 return retTree, headerTable # 返回FP树和字母表 36 37 def updateTree(items, inTree, headerTable, count): #将一条数据插进FP树中,类似于将一条字符串插进Trie树中 38 if items[0] in inTree.children: # 若首字母的结点存在,则直接更细该节点的计数器 39 inTree.children[items[0]].inc(count) # incrament count 40 else: # 否则 41 inTree.children[items[0]] = treeNode(items[0], count, inTree) #创建新结点,之后需要将该结点放进字母表的链表中 42 if headerTable[items[0]][1] == None: # 如果该字母首次出现,则直接将字母表的头指针指向该结点 43 headerTable[items[0]][1] = inTree.children[items[0]] 44 else: #否则,需要将其插入到合适的位置,书本的做法是尾插法 45 updateHeader(headerTable[items[0]][1], inTree.children[items[0]]) 46 if len(items) > 1: # call updateTree() with remaining ordered items 47 updateTree(items[1::], inTree.children[items[0]], headerTable, count) 48 49 def updateHeader(nodeToTest, targetNode): # 将新建的字母结点加入到字母表链的链尾,但个人认为头插法更优 50 while (nodeToTest.nodeLink != None): # Do not use recursion to traverse a linked list! 51 nodeToTest = nodeToTest.nodeLink 52 nodeToTest.nodeLink = targetNode
三.从一颗FP树中挖掘频繁项集
1.算法步骤
初始化:将“当前频繁项集合的前缀”设为空。
枚举生成FP树时附带生成的字母表:
1)将枚举到的字母添加到“当前频繁项集合的前缀”的末尾,这时我们就挖掘到了一个频繁项集,把它存起来。
2)在FP树中寻找该字母所有的前缀被称为“条件模式基”(管他叫什么呢),接着利用这些前缀构建一棵FP树,同时也得到了字母表。
3)如果树不为空,则对这棵新的FP树进行挖掘(此时更新的参数有:FP树、字母表、“当前频繁项集合的前缀”),这是一个递归的形式。
2.算法详解:
1)关于递归地创建FP树:
假如在递归的第一层,当前枚举到的字母为A,A在树中出现了几次,且都在树的内部。这是我们实质上是挖掘到了一个频繁项集的,那就是{}+A,而这个{}就是“当前频繁项集合的前缀”。之后在FP树中将字母A的所有前缀都取出来,对于其中一条被取出来的前缀,它的实际就是“某条数据的子集”,之后将他们组成另一棵FP树。在构建FP树的过程中,需要重新“统计”、“剔除”、“排序”,因为原本在旧FP树中某些字母的出现频率符合要求,但在新的FP树由于只是选出了部分路径而漏了其他,所以可能导致字母的频率低于阈值,或者字母的排位发生了变化。对于新构建的FP树,我们可知其是在“共有频繁项集A”的情况下的FP树,即这个FP树是有“前提条件”或者说是有“状态”的。在这棵新的FP树,我们继续枚举字母表的字母,假设枚举到字母B,那么我们又挖掘到了一个频繁项集,那就是{A}+B。以此递归地枚举下去,就可以挖掘出所有的频繁项集了。
2)关于挖掘到的频繁项集是否有重复的问题:
由于形成FP树的“数据条”里面的字母是排序过的,所在FP树中,祖先与子孙的关系是严格确定了的。出现频率高的为祖先,低的为子孙,所以在一条从根节点到叶子结点的路径中,如果A出现在B的前面,那么在B的后面,A是绝对不会出现的。简而言之:假如A的频率高于B的频率,那么所有的A必定出现在B的上面。这一点就保证了频繁项集不会有重复。
3.代码注释:
1 def updateHeader(nodeToTest, targetNode): # 将新建的字母结点加入到字母表链的链尾,但个人认为头插法更优 2 while (nodeToTest.nodeLink != None): # Do not use recursion to traverse a linked list! 3 nodeToTest = nodeToTest.nodeLink 4 nodeToTest.nodeLink = targetNode 5 6 def ascendTree(leafNode, prefixPath): #在FP树,从一个结点开始,上溯至根节点,并记录路径。这样就找到了频繁项的一个前缀路径 7 if leafNode.parent != None: 8 prefixPath.append(leafNode.name) 9 ascendTree(leafNode.parent, prefixPath) 10 11 def findPrefixPath(treeNode): # 在FP树,找出某个字母所有的前缀路径,即找到对应的条件模式基 12 condPats = {} #存储前缀路径,为何要用字典的形式?因为还要记录每条前缀路径的出现次数,然后又用来创建FP树 13 while treeNode != None: 14 prefixPath = [] #保存当前的前缀路径 15 ascendTree(treeNode, prefixPath) 16 if len(prefixPath) > 1: #因为该节点也被加进了路径当中,所以需要路径的长度大于1 17 condPats[frozenset(prefixPath[1:])] = treeNode.count #将前缀路径并其出现次数存起来 18 treeNode = treeNode.nodeLink #沿着字母表链,走向下一个结点,继续寻找前缀路径 19 return condPats 20 21 '''递归地从FP树中挖掘频繁项集,headerTable为字母表,preFix为当前频繁项集合的前缀, freqItemList用于存储频繁项集''' 22 def mineTree(inTree, headerTable, minSup, preFix, freqItemList): 23 bigL = [v[0] for v in sorted(headerTable.items(), key=lambda p: p[1])] # 对字母表进行排序(根据出现次数),但为什么 要排序呢? 24 for basePat in bigL: # 枚举字母表中的每一个字母 25 newFreqSet = preFix.copy() 26 newFreqSet.add(basePat) #将该字母加入到“当前频繁项集合的前缀”中,形成新的频繁项集 27 freqItemList.append(newFreqSet) #保存新的频繁项集 28 condPattBases = findPrefixPath(headerTable[basePat][1]) #在当前FP树中找到该字母的条件模式基 29 myCondTree, myHead = createTree(condPattBases, minSup) # 然后利用条件模式基创建新的FP树 30 if myHead != None: # 如果裁剪过后的FP树仍不为空,则将新的频繁项集作为“当前频繁项集合的前缀”,然后在新的FP树上继续挖掘频繁项集 31 mineTree(myCondTree, myHead, minSup, newFreqSet, freqItemList)