问题 L: 超超的中等意思

题目描述

已知p,q,k和一个难搞得多项式(px+qy)^k。想知道在给定a和b的值下计算多项式展开后x^a*y^b得系数s。

输入

多组输入，每组数据一行输入p,q,k,a,b。其中保证k = a+b，所有输入都为非负数且不大于50000

输出

输出系数s对2^61-1取模后的值

样例输入 Copy

1 1 2 1 1

样例输出 Copy

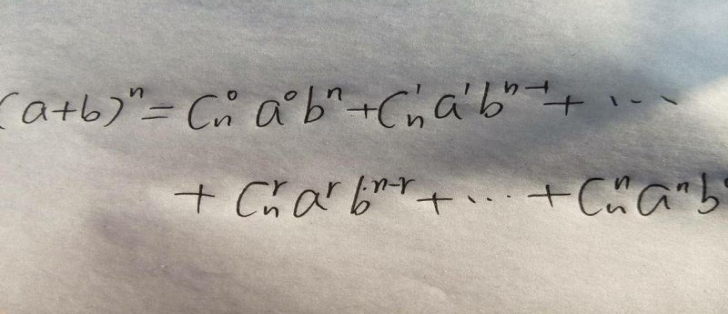
式子我们很容易就可以得知我们要求的是那个系数，答案也就是求组合数*x 的系数的 a 次方*y 的系数的 b 次方，

根据这个

我们在计算次方的时候可以用快速幂节约时间，组合数也可以由 C（m+1,n+1）

=C(m,n)+C(m+1,n)递推打表

 1 #include<iostream>
 2 #include<cmath>
 3 //using namespace std;
 4 //#include <iostream>
 5 #include<string.h>
 6 #include <stdio.h>
 7 #define ll long long
 8 typedef __int128 lll;
 9 const lll MOD = 2305843009213693951;
10 using namespace std;
11 const int N = 10000;
12 lll nn[N],mm[N];
13 
14 
15  lll dp[50020][50020];
16 void D()
17 {
18   lll n, k;
19     dp[1][1] = 1;
20     for(int i = 1; i < 50010; i++)
21     {
22         dp[i][0] = 1;
23     }
24     for(int i = 2; i < 50010; i++)
25     {
26         for(int j = 1; j <= i; j++)
27             dp[i][j] = dp[i - 1][j] + dp[i - 1][j - 1];
28     }
29     //int n, k;
30     //while(scanf("%d %d", &n, &k) == 2)
31    // {
32         //printf("%d
", dp[n][k]);
33    // }
34    return ;
35   //  return 0;
36 }
37 lll C(lll n,lll m)
38 {
39     if(m==0||n==m) return 1;
40     lll sb=min(m,n-m);
41     lll f=1,f1;
42     for(lll i=1;i<=sb;i++)
43     {
44         f1=f*(n-i+1)/(i);
45         f=f1;
46     }
47     return f1;
48 }
49 lll pow64(lll x, lll y) {
50      
51     if(!y) return 1;
52     if(x >= MOD) x %= MOD;
53     lll ans = 1;
54     while(y) {
55          
56         if(y & 1) ans = ans * x % MOD;
57         x = x * x % MOD;
58         y >>= 1;
59          
60     }
61     return ans;
62      
63 }
64 int main()
65 {
66     int p,q,k,a,b;
67 //    D();
68         while(scanf("%d%d%d%d%d",&p,&q,&k,&a,&b)!=EOF){
69     
70    // long long m,n;
71 //    while(cin>>m>>n)///C(m,n)
72 //    {
73        // cout<<C[m][n]<<endl;
74 //    }
75 //int c = (int)C(m,n);
76 //int l = (int)pow(p,b);
77 //int f = (int)pow(q,n);
78 //prlong longf("%lld",(long long)pow(p,b));
79 printf("%lld
",ll(pow64(p, a) * pow64(q, b) % MOD * C(k, a) % MOD));
80    // return 0;
81 }
82 }

View Code