不用说这两位都是冷门算法……毕竟O(n^3)的时间复杂度算法在算法竞赛里基本算是被淘汰了……而且也没有在这个算法上继续衍生出其他的算法…
有兴趣的话:click here..
话说学离散的时候曾经有个把warshall算法简化到1/2时间的想法……不过懒得去翻了,现在想想本来这两个不用矩阵而用位运算的话速度不知道比我那个方法快多少倍……
嘛,切入正题吧,先讲warshall算法,其用来计算有向图的传递闭包,不知道概念的请去百度(躺
之前在学离散的时候还是花了点时间来研究这个算法的,但是仔细看了下书上的就发现和书上写的有些不一样,下面讲讲我知道的那种和书上的那种:
我知道的那种:
将有向图的邻接矩阵进行相乘操作,每乘一次保存结果,原本的矩阵称为R(1),再乘以R(1)称为R(2),再乘以R(1)称为R(3)…直到取到R(n-1)为止。将R1….Rn-1取并,得出相连矩阵结果。
原理,易证,将邻接矩阵相乘所得为比当前路线高一阶的相连矩阵,假设R1为所有路径为1的通路,那么R2就是所有路径为2的通路。。。Rn-1就是所有路径为n-1的通路。因为只有n个节点,假设求得路线不存在环,那最多为n-1长度,可从之前结果获得,假设存在环,那么环的结果再之前便已经取得。无论怎样,其并结果绝对包含所有节点的链接关系。
书上新看到的:
for k in vertex
for i in row
for j in col
如果点i,k.col存在相连关系,k.row,j存在相连关系,那么这个点就是可以被连上的。
同样的,floyd也是这个尿性,不过里面得改一下:
若能相连,看看是不是比现在的值小,小的就换上。
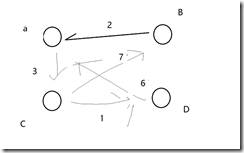
嘛,怎么说肯定不是很理解,所以我就用例子说明一下把:
这样的一张图,邻接矩阵的样式为:
a b c d
a 0 n 3 n
b 2 0 n n
c n 7 0 1
d 6 n n 0
布尔值的样式是:
a b c d
a 0 n 1 n
b 1 0 n n
c n 1 0 1
d 1 n n 0
那么,warshall的做法是,先统计第1行和第1列,发现(d,c)列对应的(a,c)(第一行),和(d,a)(第一列)都为1,则(d,c)变为1,同理,(b,c)变为1,那么第一轮的结果是:
a b c d
a 0 n 1 n
b 1 0 1 n
c n 1 0 1
d 1 n 1 0
第二轮:
a b c d
a 0 n 1 n
b 1 0 1 n
c 1 1 1 1
d 1 n 1 0
第三轮:
a b c d
a 1 1 1 1
b 1 1 1 1
c 1 1 1 1
d 1 1 1 1
至此,已经没有进行第四轮的必要,故这是一个全通图。floyd的思路与其类似,不过是判断是否两个关联值加起来是否小于当前值,小于的话那就更新,不然不更新。