今天的考试有结束了,又一次被右边的同桌虐了(额,排名第三的大佬)但是考试还是进步了一名,算是有进步吧
成绩:
那个12名就是我,一个AC都没有,太难受了。
T1:
题目链接:http://hzoi.com/contest/39/ranklist/1(内部题库,不确保能进入)
题目:
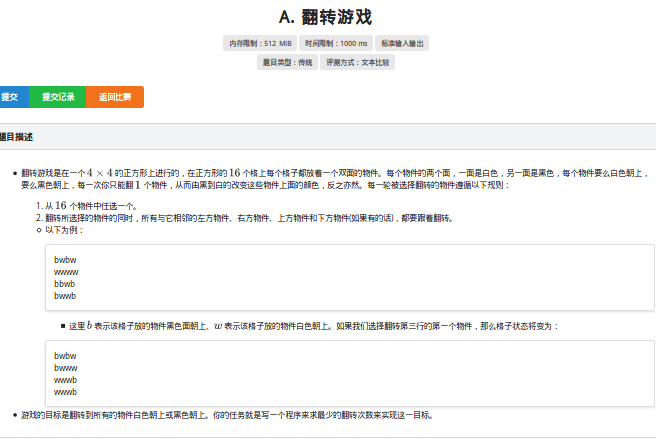
题目是一个简化版,很水,直接2的16次方枚举就完了。
当时不知到咋回事居然TLE 60(尬);
直接看代码吧:
#include <cstdio>
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
//monsters;
int a[5][5],data[5][5];
int lowbit(int x){
return x&-x;
}
int get(int x){
int num=0;
for(int j=x;j>0;j-=lowbit(j)){
num++;
}
return num;
}
void gai(int x,int y){
a[x][y]^=1;
a[x+1][y]^=1;
a[x-1][y]^=1;
a[x][y-1]^=1;
a[x][y+1]^=1;
}
void clear(){
for(int i=1;i<=4;i++){
for(int j=1;j<=4;j++){
a[i][j]=data[i][j];
}
}
}
bool pan(){
int c=a[1][1];
for(int i=1;i<=4;i++){
for(int j=1;j<=4;j++){
if(a[i][j]!=c)return 0;
}
}
return 1;
}
int main(){
// freopen("a.in","r",stdin);
std::ios::sync_with_stdio(false);//cin cout 的优化
std::cin.tie(0);
for(int i=1;i<=4;i++){//预处理
for(int j=1;j<=4;j++){
char c;cin>>c;
if(c=='b')a[i][j]=data[i][j]=1;
else a[i][j]=0;
}
}
int ans=110;
for(int i=0;i<(1<<16);i++){//暴力枚举每个点是否翻转 1翻转 0 不反转
int cnt=get(i);
int num=0;
int j=i;
while(i>0){
if((i&1)==1){
int x=num/4+1;int y=(num+4)%4+1;//计算出点的坐标
gai(x,y);
}
num++;
i=i>>1;
}
if(pan()){
//printf("%d ",cnt);
ans=min(ans,cnt);
}
clear();
i=j;
}
if(ans==110){
cout<<"Impossible";return 0;
}
cout<<ans;
return 0;
}
当然还有更加优化的做法,详见洛谷P1764
T2:
题目来自于洛谷P3627[APIO2009] 题目链接:https://www.luogu.com.cn/problem/P3627
题目: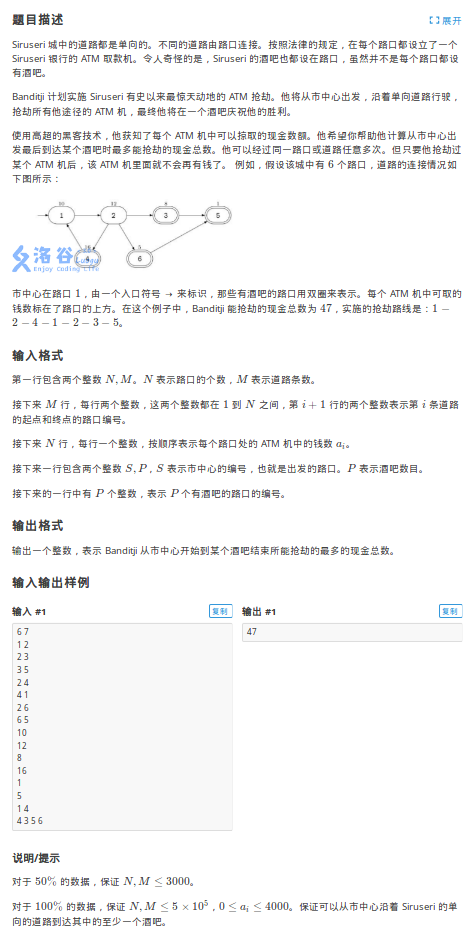
这题太水了,一眼救出思路:Tarjan+最短路
当时我忘了跑最短路,直接爆搜的,TLE 80pts.
几个注意点:
1.最短路能用Dij ,不符合DIj 原理。
2.实际上是个最长路,可以点权变负再跑。
OK 代码:
#include<cstdio>
#include<algorithm>
#include<queue>
using namespace std;
const int maxn=500005;
struct edge{
int from,to,next;
}e[500005];
struct node{
int to,next;
}v[500005];
int vhead[maxn],cnt;
int head[maxn],ans,shu[maxn];
void insert(int x,int y){
e[++ans].from=x;e[ans].to=y;e[ans].next=head[x];head[x]=ans;
}
int dfn[maxn],low[maxn],dfs_clock;
int sta[maxn],top,belong[maxn],scc_cnt,siz[maxn];
void dfs(int u){
dfn[u]=low[u]=++dfs_clock;
sta[++top]=u;
for(int i=head[u];i;i=e[i].next){
int v=e[i].to;
if(!dfn[v]){
dfs(v);
low[u]=min(low[u],low[v]);
}else if(!belong[v])low[u]=min(low[u],dfn[v]);
}
if(dfn[u]==low[u]){
++scc_cnt;
while(1){
int x=sta[top--];
belong[x]=scc_cnt;
siz[scc_cnt]+=shu[x];
if(x==u)break;
}
}
}
int dis[500005],scnt[500005],ing[500005];
queue<int> q;
bool SPFA(int s,int n){
for(int i=1;i<=n;i++){
dis[i]=0x3f3f3f3f;scnt[i]=0;
}
scnt[s]=1;dis[s]=siz[s];q.push(s);ing[s]=1;
while(!q.empty()){
int u=q.front();q.pop();ing[u]=0;
for(int i=vhead[u];i;i=v[i].next){
int t=v[i].to;
if(dis[t]>dis[u]+siz[t]){
dis[t]=dis[u]+siz[t];
if(!ing[t]){
if(++scnt[t]>=n)return 0;
ing[t]=1;q.push(t);
}
}
}
}
return 1;
}
int main(){
int n,m;scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++){
int x,y;scanf("%d%d",&x,&y);
insert(x,y);
}
for(int i=1;i<=n;i++){
int x;scanf("%d",&x);
shu[i]=-x;
}
int s,p;scanf("%d%d",&s,&p);
dfs(s);
for(int i=1;i<=m;i++){
int x=e[i].from,y=e[i].to;
if(belong[x]!=belong[y]){
v[++cnt].to=belong[y];
v[cnt].next=vhead[belong[x]];
vhead[belong[x]]=cnt;
}
}
int flag=SPFA(belong[s],scc_cnt);
int Max=-1;
for(int i=1;i<=p;i++){
int x;scanf("%d",&x);
Max=max(Max,-dis[belong[x]]);
}
printf("%d",Max);
return 0;
}
T3:
题目来源:洛谷P2933 [USACO09JAN]The Baric Bovine G 链接:https://www.luogu.com.cn/problem/P2933

这道题其实挺难的。
一开始首先想DFS暴搜,后来算一下100!发现不现实。
那么只能想 DP 了
首先只能定义状态:
f[i][j]为前i个书选择j个的最小误差。
显然的f[i][j]=min(f[i][j],f[k][j-1]+?);
那么?是啥?
我们可以预处理出数组pre[i][j] 表示 原序列 中 Mi ,Mj 是所选的的相邻的两个元素,则i 到 j 之间元素对误差的贡献 ,显然我们可以n3暴力枚举 轻松得出
我们用pre[i][0] 表示如果Mi 是序列第一个数,则M1 ——Mi-1 的误差之和,同理pre[i][n+1] 表示Mi 作为最后一个元素的情况。
然后就可以转移了。
f[i][j]=min(f[i][j],f[k][j-1]-pre[k][n+1]+pre[i][n+1]+pre[k][i]);
然后有一些细节代码中展示
代码:
#include <cstdio>
#include <cmath>
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int maxn=105;
int n,m;
int a[maxn],pre[maxn][maxn];
int f[maxn][maxn];
int cnt=101,Max=0x3f3f3f3f;
int main(){
//freopen("a.in","r",stdin);
std::ios::sync_with_stdio(false);
std::cin.tie(0);
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>a[i];
}
for(int i=1;i<=n;i++){
for(int j=i+1;j<=n;j++){
for(int k=i+1;k<j;k++){
pre[i][j]+=abs(2*a[k]-a[i]-a[j]);
}
}
}
for(int i=1;i<=n;i++){
for(int k=1;k<i;k++){
pre[i][0]+=2*abs(a[k]-a[i]);
}
}
for(int i=1;i<=n;i++){
for(int k=i+1;k<=n;k++){
pre[i][n+1]+=2*abs(a[k]-a[i]);
}
}
for(int i=1;i<=n;i++){
f[1][i]=pre[i][0]+pre[i][n+1];
if(f[1][i]<=m){
cnt=1;Max=min(Max,f[1][i]);
}
}
if(cnt==1){
cout << cnt <<' '<< Max;return 0;
}
for(int i=2;i<=n;i++){
for(int j=i;j<=n;j++){
f[i][j]=0x3f3f3f3f;
for(int k=i-1;k<j;k++){
f[i][j]=min(f[i][j],f[i-1][k]-pre[k][n+1]+pre[j][n+1]+pre[k][j]);
}
if(f[i][j]<=m){
if(i>cnt)continue;
if(i<cnt){
cnt=i;Max=f[i][j];
}
else if(i==cnt)Max=min(Max,f[i][j]);
}
}
}
cout<<cnt<<' '<<Max;
return 0;
}
T4 :
原题来自于洛谷P3963 [TJOI2013] 奖学金 题目链接:https://www.luogu.com.cn/problem/P3963
题目:
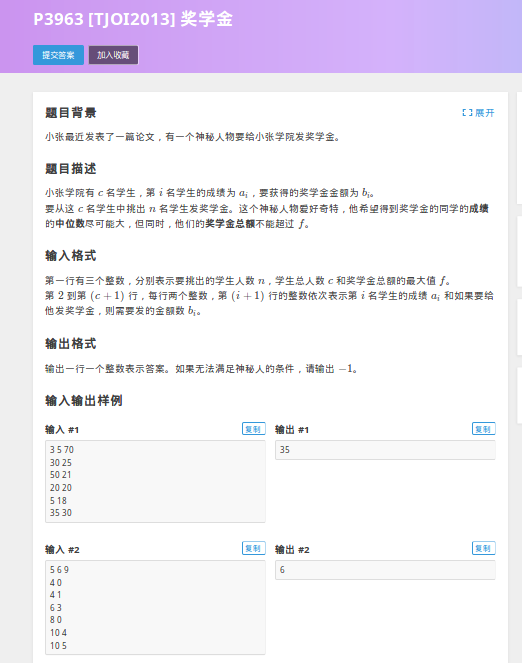
题目很好理解:我当时最先想出来了二分答案,
其实二分答案是不对的,错误样例请自己证明
那么这道题该如何做,
大家可以参考一下 洛谷上黑匣子一题
应该就会找到思路。
下面是代码:
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
#include <queue>
#define ll long long
using namespace std;
const int maxn=200005;
int n,m;ll p;
struct node{
ll dis,money;
}e[maxn];
bool cmp(node a,node b){
return a.dis<b.dis;
}
priority_queue<ll> q;
ll f[maxn],d[maxn];
int main(){
//freopen("a.in","r",stdin);
std::ios::sync_with_stdio(false);
std::cin.tie(0);
cin>>n>>m>>p;
for(int i=1;i<=m;i++){
cin>>e[i].dis>>e[i].money;
}
sort(e+1,e+m+1,cmp);
ll sum=0;
for(int i=1;i<=n/2;i++){
q.push(e[i].money);
sum+=e[i].money;
}
for(int i=n/2+1;i<=m;i++){
f[i]=sum;
int x=e[i].money;
int top=q.top();
if(top>e[i].money){
q.pop();
sum-=top;
sum+=e[i].money;
q.push(e[i].money);
}
}
sum=0;
while(q.size())q.pop();
for(int i=m;i>=m-n/2+1;i--){
q.push(e[i].money);
sum+=e[i].money;
}
for(int i=m-n/2;i>=1;i--){
d[i]=sum;
int top=q.top();
if(top>e[i].money){
q.pop();
sum-=top;
sum+=e[i].money;
q.push(e[i].money);
}
}
for(int i=m-n/2;i>=1+n/2;i--){
if(f[i]+d[i]+e[i].money<=p){
cout<<e[i].dis;return 0;
}
}
cout<<"-1";
return 0;
}
OK 今天总结到此结束了。
希望明天能冲进前十