线图
题目描述
九条可怜是一个热爱出题的女孩子。
今天可怜想要出一道和图论相关的题。在一张无向图 $G$ 上,我们可以对它进行一些非常有趣的变换,比如说对偶,又或者说取补。这样的操作往往可以赋予一些传统的问题新的活力。例如求补图的连通性、补图的最短路等等,都是非常有趣的问题。
最近可怜知道了一种新的变换:求原图的线图 (line graph)。对于无向图 $G = ⟨V, E⟩$,它的 线图 $L(G)$ 也是一个无向图:
- 它的点集大小为 $|E|$,每个点唯一对应着原图的一条边。
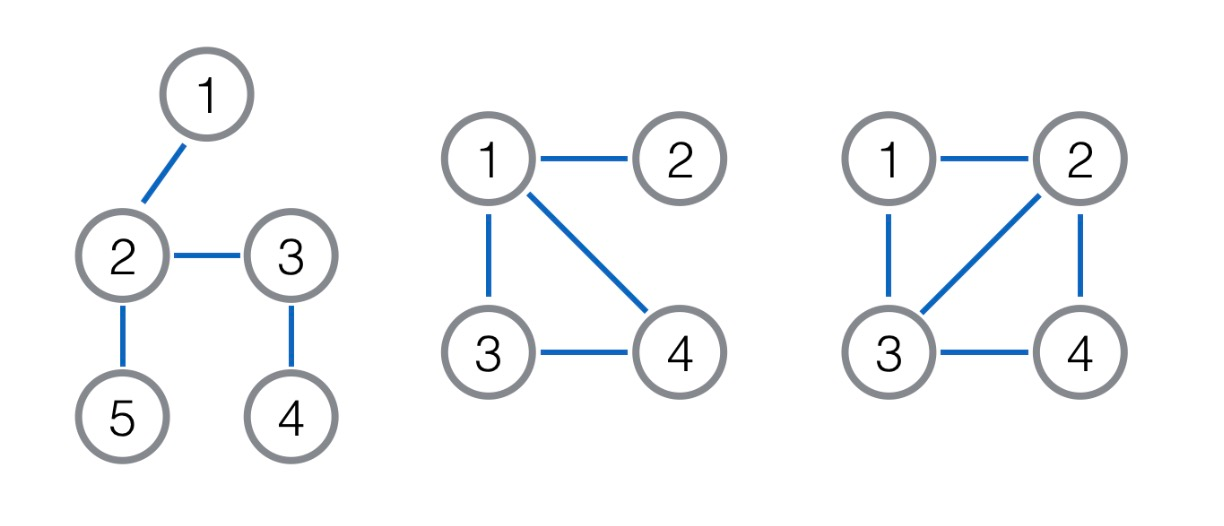
- 两个点之间有边当且仅当这两个点对应的边在原图上有公共点(注意不会有自环)。 下图是一个简单的例子,左图是原图,右图是它对应的线图。其中点 $1$ 对应原图的边 $(1, 2)$,点 $2$ 对应 $(1, 4)$,点 $3$ 对应 $(1, 3)$,点 $4$ 对应 $(3, 4)$。

经过一些初步的摸索,可怜发现线图的性质要比补图复杂很多,其中突出的一点就是补图 的补图会变回原图,而 $L(L(G))$ 在绝大部分情况下不等于 $G$ ,甚至在大多数情况下它的点数和 边数会以很快的速度增长。
因此,可怜想要从最简单的入手,即计算 $L^{k}(G)$ 的点数(其中 $L^{k}(G)$ 表示对 $G$ 求 $k$ 次线图)。 然而遗憾的是,即使是这个问题,对可怜来说还是太困难了,因此她进行了一定的弱化。她给出了一棵 $n$ 个节点的树 $T$,现在她想让你计算一下 $L^{k}(T)$ 的点数。
输入输出格式
输入格式:
第一行输入两个整数 $n$,$k$,表示树的点数以及连续求线图的次数。
接下来 $n − 1$ 行每行两个整数 $u$, $v$ 表示树上的一条边。
输出格式:
输出一行一个整数,表示答案对 $998244353$ 取模后的值。
样例一
input
5 3
1 2
2 3
2 5
3 4
output
5
explanation
如下图所示,左图为原树,中图为 $L(G)$,右图为 $L^{2}(G)$。这儿并未画出 $L^{3}(G)$,但是由于 $L^{2}(G)$ 有 $5$ 条边,因此 $L^{3}(G)$ 中有 $5$ 个点。
限制与约定
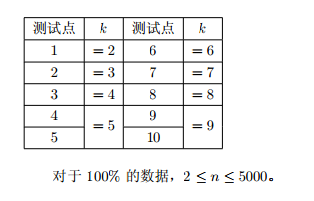
时间限制:3s
空间限制:512MB
这题的数据范围很有趣啊,谁叫标算的复杂度也是指数级的呢?
假如用人类智慧是容易做出前 30 分的,高水平的选手再发现一些性质能拿到 50 分,而显然我并不是,因为我在考场上只有 20 分。
那我们来看一看线图的高妙之处:
考虑 $L^{k}(G)$ 中的每一个点在 $G$ 中代表的形状。
- 显然,$L(G)$ 的点数对应了原图中的一条边。
- 容易发现,$L^{2}(G)$ 的点数对应了原图中的一条折线(即一对相邻的两条边)。
- 稍加推敲得到,$L^{3}(G)$ 的点数对应了原图中的一条长度为三的链或一组相互相邻的三条边。
以此类推不难发现,在 $L^{k}(G)$ 中的每一个点对应的是 $G$ 中的一个不超过 $k$ 条边的联通导出子图。由于原图 $G$ 是棵树,所以 $L^{k}(G)$ 中每一个点对应的是 $G$ 中的一颗边数不超过 $k+1$ 的子树。一个简单的结论是:两个结构相同(即同构)的导出子图,它们在 $L^{k}(G)$ 中对应的节点个数一定也是相同的。
于是我们考虑了一个初步的做法:
- 枚举所有的边数不超过 $k+1$ 的无根树,假设为 $T_{i}$,算出 $T_{i}$ 在 $L^{k}(G)$ 中对应的点数 $w_{i}$。
- 算出 $T_{i}$ 在 $G$ 中出现了的次数 $t_{i}$。
- $Ans = sumlimits_{T_{i}}^{} w_{i} * t_{i}$。
枚举不同构的有根树可以枚举括号序列然后用树哈希来去重,因此主要考虑给定 $T_{i}$,如何 求解 $w_{i}$ 和 $t_{i}$。
求解 $w_{i}$ :
因为 $T_{i}$ 的大小很小,我们能够求解 $L^{k}(T_{i})$ 的点数。但是这并不是我们要求的 $w_{i}$,因为这中的每一个点对应了 $T_{i}$ 中的每一个联通子图,也就是说这中间有 $T_{i}$ 的子图的贡献,我们需要减掉它们,我们可以 $O(2^{|T_{i}|})$ 枚举 $T_{i}$ 的子图,减掉它们的贡献,计算出 $w_{i}$ 的值。
容斥的复杂度并不是瓶颈,关键在于现在考虑如何求出 $L^{k}(T_{i})$ 的点数,如果暴力做的话,复杂度大概是 $O(k^{k})$,不太行。
我们可以沿用之前做部分分时的做法:
- $L(T_{i})$ 的点数是 $m$。
- $L^{2}(T_{i})$ 的点数是 $sumlimits_{i in V}^{} C_{d_{i}}^{2}$,其中 $d_{i}$ 为 $i$ 的度数。
- $L^{3}(T_{i})$ 的点数是 $sumlimits_{(u,v) in E}^{} (d_{u}-1)(d_{v}-1) + sumlimits_{i in V}^{} C_{d_{i}}^{3}$
- $L^{4}(T_{i})$ 的点数同样也可以用人类智慧直接算出来。
这样我们就只需要算 $L^{k-4}(T_{i})$ 就可以了。
这里有一个可以剪枝的地方,就是曾经算过的无根树与当前有同构时,就不必再算了。
求解 $t_{i}$:
想要直接把 $T_{i}$ 当无根树计算出它在另一个无根树 $G$ 中出现的次数是很难的,毕竟无根树的计数比有根树更复杂。
我们可以发现,如果我们把两颗无根树都当成有根树来做,即枚举有根树,却也是对的。因为无根树在另一颗无根树上一个成功的匹配,我们把某一棵无根树拉成有根树,另一棵无根树此时呈现出的有根形态一定会被枚举到恰好一次。于是问题得到了简化。
我们可以用树形dp直接解决它,由于 $T_{i}$ 的大小很小,用状压dp就可以了。
令 $f_{i,j}$ 为 $G$ 上第 $i$ 个点为第 $j$ 种有根树的根的嵌入方案数。
由于 $j$ 的孩子中可能存在两棵同构的子树,由于是没有标号的,故答案只能算一次,这是在dp时要注意的。然而我的实现方法并不优越,我的做法是,暴力合并所有同构的子树,每次dp时枚举之前所有状态中不包含这些同构子树中任意一个的状态。于是我就枚举子集了,复杂度变劣了一点。
然而在dp中有很多可以剪枝的地方,比如很显然,$i$ 的孩子数肯定不会少于 $j$ 的儿子数,或者在 $T_{i}$ 中存在一个子树和 $j$ 的子树同构,那可以不用重复计算了。
最后还有一个优化,就是当 $j$ 的亲生儿子中有叶子节点时,可以不用状压进去,直接用组合数算就可以啦。
于是我们就解决的这道题了,我在UOJ上勉强卡过去了,UOJ跑得还挺快的呢!反正我本地T飞了

1 #include <cstdio> 2 #include <map> 3 #include <cmath> 4 #include <cstdlib> 5 #include <cstring> 6 #include <vector> 7 #include <iostream> 8 #include <algorithm> 9 using namespace std; 10 11 typedef long long LL; 12 typedef pair<int, int> Pair; 13 #define fir first 14 #define sec second 15 #define Mp make_pair 16 typedef vector<int>::iterator Vecit; 17 typedef vector<Pair>::iterator Vecpa; 18 19 const int N = 5005, MOD = 998244353, M = 11, NM = 110005; 20 21 int Ans; 22 int n, K; 23 int fa[N], A[1<<23], pd[M][M], C[N][23]; 24 int dg[NM], dgr[NM], dgs[NM]; 25 int dp[N][M], gp[2][1<<M]; 26 27 vector<Pair> E, B[NM]; 28 vector<int> G[N], T[N]; 29 inline void Add(int a, int b) { 30 G[a].push_back(b); 31 } 32 33 inline void Ad(int &a, int b) { 34 a+=b; 35 (a>=MOD)? (a-=MOD):(0); 36 } 37 inline int Last_pos(int x, int res=0) { 38 for (x&=(-x); x; x>>=1) ++res; return res; 39 } 40 inline int Count(int x, int res=0) { 41 for (; x; x>>=1) res+=x&1; return res; 42 } 43 #define Sqr(x) ((LL)(x)*(x)) 44 #define _c2(x) ((LL)(x)*((x)-1)/2) 45 46 inline int Calc(int n, int m, int K, int res=0) { 47 if (K==1) return m; 48 memset(dg, 0, sizeof(int)*(n+1)); 49 memset(dgr, 0, sizeof(int)*(n+1)); 50 memset(dgs, 0, sizeof(int)*(n+1)); 51 for (Vecpa p=E.begin(); p!=E.end(); ++p) ++dg[(*p).fir], ++dg[(*p).sec]; 52 if (K==2) { 53 for (int *i=dg+1; i<=dg+n; ++i) res=(res+_c2(*i))%MOD; 54 return res; 55 } 56 if (K==3) { 57 for (Vecpa p=E.begin(); p!=E.end(); ++p) 58 res=(res+_c2(dg[(*p).fir]+dg[(*p).sec]-2))%MOD; 59 return res; 60 } 61 if (K==4) { 62 for (Vecpa p=E.begin(); p!=E.end(); ++p) { 63 int u=(*p).fir, v=(*p).sec, X=dg[u]+dg[v]-2; 64 dgr[u]=(dgr[u]+(LL)X*X)%MOD; 65 dgr[v]=(dgr[v]+(LL)X*X)%MOD; 66 Ad(dgs[u], X); 67 Ad(dgs[v], X); 68 } 69 for (int i=1; i<=n; ++i) { 70 int sqr=dgr[i], sum=dgs[i], deg=dg[i]; 71 res=(res+(LL)sum*sum-sqr+(LL)sqr*(deg-1)-(LL)5*(deg-1)*sum+(LL)6*_c2(deg))%MOD; 72 } 73 return (LL)res*(MOD+1)/2%MOD; 74 } 75 int cnt=0; 76 for (int i=0; i<=n; ++i) B[i].clear(); 77 for (Vecpa p=E.begin(); p!=E.end(); ++p) { 78 B[(*p).fir].push_back(Mp((*p).sec, ++cnt)); 79 B[(*p).sec].push_back(Mp((*p).fir, cnt)); 80 } 81 E.clear(); 82 for (int i=1; i<=n; ++i) 83 for (int j=0; j<(int)B[i].size(); ++j) 84 for (int k=0; k<j; ++k) 85 E.push_back(Mp(B[i][j].sec, B[i][k].sec)); 86 return Calc(m, (int)E.size(), K-1); 87 } 88 89 inline void Get_dp(int x, int Fa, int K) { 90 for (Vecit p=G[x].begin(); p!=G[x].end(); ++p) if (*p!=Fa) { 91 Get_dp(*p, x, K); 92 } 93 for (int i=1; i<=K; ++i) { 94 int flg=0; 95 for (int j=1; j<i; ++j) if (pd[i][j]) { 96 dp[x][i]=dp[x][j]; flg=1; break; 97 } 98 if (flg) continue; 99 int cnt=0; 100 vector<int> L; 101 for (Vecit p=T[i].begin(); p!=T[i].end(); ++p) if (*p!=fa[i]) { 102 if ((int)T[*p].size()==1) ++cnt; 103 else L.push_back(*p); 104 } 105 if (cnt+(int)L.size() > (int)G[x].size()-(x!=1)) continue; 106 int ST=1<<(int)L.size(), ls=0, no=1; 107 memset(gp[0], 0, sizeof(int)*(ST)); 108 memset(gp[1], 0, sizeof(int)*(ST)); 109 gp[no][0]=1; 110 for (Vecit v=G[x].begin(); v!=G[x].end(); ++v) if (*v!=Fa) { 111 int ns=0; 112 for (int j=0; j<(int)L.size(); ++j, ns=0) if (dp[*v][L[j]]){ 113 for (int k=0; k<j; ++k) if (pd[L[j]][L[k]]) ns|=1<<k; 114 int U=(ST-1)^ns^(1<<j); 115 for (int sub=U; sub; sub=(sub-1)&U) { 116 Ad(gp[ls][sub|ns|(1<<j)], (LL)dp[*v][L[j]]*gp[no][sub|ns]%MOD); 117 } 118 Ad(gp[ls][ns|(1<<j)], (LL)dp[*v][L[j]]*gp[no][ns]%MOD); 119 } 120 for (int st=0; st<ST; ++st) { 121 Ad(gp[ls][st], gp[no][st]), gp[no][st]=0; 122 } 123 no^=1; ls^=1; 124 } 125 dp[x][i]=(LL)gp[no][ST-1]*C[(int)G[x].size()-(int)L.size()-(x!=1)][cnt]%MOD; 126 } 127 } 128 129 string Hash_tree(int x, int st, int Fa) { 130 vector<string> v; 131 for (Vecit p=T[x].begin(); p!=T[x].end(); ++p) { 132 if (*p!=Fa && (st>>(*p-1))&1) v.push_back(Hash_tree(*p, st, x)); 133 } 134 sort(v.begin(), v.end()); 135 string res=""; 136 for (int i=0; i<(int)v.size(); ++i) res+='1'+v[i]+'0'; 137 return res; 138 } 139 140 inline int Hash_to_int(string s) { 141 int res=0, le=s.length(); 142 for (int i=0; i<le; ++i) res=(res<<1)|(s[i]=='1'); 143 return res; 144 } 145 146 inline int Build_tree(string tree, int K) { 147 int x=1, cnt=1, le=tree.length(); 148 for (int i=0; i<le; ++i) 149 if (tree[i]=='0') { 150 x=fa[x]; 151 if (!x) return -1; 152 } else { 153 fa[++cnt]=x; 154 T[x].push_back(cnt); 155 T[cnt].push_back(x); 156 E.push_back(Mp(x, cnt)); 157 x=cnt; 158 if (x>K) return -1; 159 } 160 if (x!=1) { 161 cerr << tree << endl; 162 exit(13); 163 } 164 return cnt; 165 } 166 167 168 typedef unsigned long long ULL; 169 map<ULL, int> Map; 170 ULL get_hash(int n) { 171 ULL ret=0; 172 vector<int> v; 173 for (int i=1; i<=n; ++i) { 174 v.push_back(Hash_to_int(Hash_tree(i, (1<<n)-1, 0))); 175 } 176 sort(v.begin(),v.end()); 177 for (int i=0; i<n; ++i) ret=ret*19260817+v[i]; 178 return ret; 179 } 180 181 182 void DFS(string tree, int K) { 183 if ((int)tree.length() < 2*(K-1)) { 184 DFS(tree+'1', K); 185 DFS(tree+'0', K); 186 return; 187 } 188 E.clear(); 189 for (int i=0; i<=K; ++i) T[i].clear(); 190 if (Build_tree(tree, K) != K) return; 191 int ss=Hash_to_int(Hash_tree(1, (1<<K)-1, 0)); 192 if (~A[ss]) return; 193 ULL haha=get_hash(K); 194 A[ss]=(Map.count(haha)? Map[haha] : Map[haha]=Calc(K, K-1, ::K)); 195 196 for (int st=0; st<(1<<K)-1; ++st) { 197 string gt=Hash_tree(Last_pos(st), st, 0); 198 if ((int)gt.length() != 2*(Count(st)-1)) continue; 199 A[ss]=(A[ss]-A[Hash_to_int(gt)]+MOD)%MOD; 200 } 201 memset(pd, 0, sizeof pd); 202 for (int i=1; i<=K; ++i) 203 for (int j=i+1; j<=K; ++j) 204 pd[i][j]=pd[j][i]=(Hash_tree(i, (1<<K)-1, fa[i]) == Hash_tree(j, (1<<K)-1, fa[j])); 205 for (int i=1; i<=n; ++i) 206 memset(dp[i], 0, sizeof(int)*(K+1));; 207 Get_dp(1, 0, K); 208 int res=0; 209 for (int i=1; i<=n; ++i) Ad(res, dp[i][1]); 210 Ad(Ans, (LL)A[ss]*res%MOD); 211 } 212 213 int main() { 214 memset(A, -1, sizeof A); 215 scanf("%d%d", &n, &K); 216 for (int i=1, x, y; i<n; ++i) { 217 scanf("%d%d", &x, &y); Add(x, y); Add(y, x); 218 } 219 220 for (int i=0; i<=n; ++i) { 221 C[i][0]=1; 222 for (int j=1; j<=i && j<=20; ++j) C[i][j]=(C[i-1][j]+C[i-1][j-1])%MOD; 223 } 224 225 for (int i=1; i<=K+1; ++i) DFS("", i); 226 printf("%d ", Ans); 227 228 return 0; 229 }
