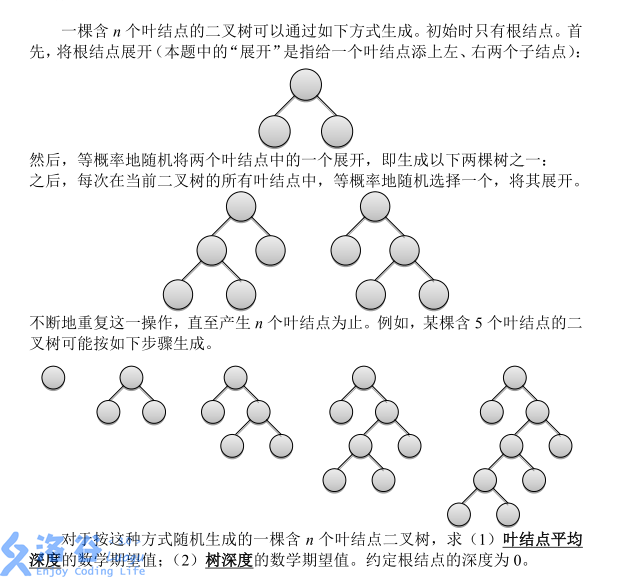
Description
(nle 100)
Solution
Problem 1
不难看出,答案就是:
[1+sum_{i=1}^{n-1} 2/(i+1)
]
Problem 2
这个问真的很仙。
可(bu)以(neng) 想到,我们可以设 (f_{i,j}) 表示有 (i) 个叶子时深度 (ge j) 的概率,可以得到转移式:
[f_{i,j}=frac{1}{i-1}sum_{k=1}^{i-1} (f_{k,j-1}+f_{i-k,j-1}-f_{k,j-1} imes f_{i-k,j-1})
]
可以直接除以 (i-1) 是因为可以证明把两颗子树合并,只要总大小相同,那么方案就相同。这里就不赘述了。
然后我们就可以得到答案就是:
[sum_{i=1}^{n-1} (f_{n,i}-f_{n,i+1}) imes i
]
Code
#include <bits/stdc++.h>
using namespace std;
#define Int register int
#define MAXN 105
template <typename T> inline void read (T &t){t = 0;char c = getchar();int f = 1;while (c < '0' || c > '9'){if (c == '-') f = -f;c = getchar();}while (c >= '0' && c <= '9'){t = (t << 3) + (t << 1) + c - '0';c = getchar();} t *= f;}
template <typename T,typename ... Args> inline void read (T &t,Args&... args){read (t);read (args...);}
template <typename T> inline void write (T x){if (x < 0){x = -x;putchar ('-');}if (x > 9) write (x / 10);putchar (x % 10 + '0');}
double f[MAXN][MAXN];
signed main(){
int q,up;read (q,up);
if (q == 1){
double d = 1;
for (Int n = 2;n < up;++ n) d += 2.0 / (n + 1);
printf ("%.6f
",d);
}
else{
for (Int i = 1;i <= up;++ i) f[i][0] = 1;
for (Int i = 2;i <= up;++ i)
for (Int j = 1;j < i;++ j){
for (Int k = 1;k < i;++ k) f[i][j] += f[k][j - 1] + f[i - k][j - 1] - f[k][j - 1] * f[i - k][j - 1];
f[i][j] /= (i - 1);
}
double d = 0;
for (Int i = 1;i < up;++ i) d += (f[up][i] - f[up][i + 1]) * i;
printf ("%.6f
",d);
}
return 0;
}