题目描述
你在一家 IT 公司为大型写字楼或办公楼(offices)的计算机数据做备份。然而数据备份的工作是枯燥乏味的,因此你想设计一个系统让不同的办公楼彼此之间互相备份,而你则坐在家中尽享计算机游戏的乐趣。
已知办公楼都位于同一条街上。你决定给这些办公楼配对(两个一组)。每一对办公楼可以通过在这两个建筑物之间铺设网络电缆使得它们可以互相备份。
然而,网络电缆的费用很高。当地电信公司仅能为你提供 K 条网络电缆,这意味着你仅能为 K 对办公楼(或总计 2K 个办公楼)安排备份。任一个办公楼都属于唯一的配对组(换句话说,这 2K 个办公楼一定是相异的)。
此外,电信公司需按网络电缆的长度(公里数)收费。因而,你需要选择这 K对办公楼使得电缆的总长度尽可能短。换句话说,你需要选择这 K 对办公楼,使得每一对办公楼之间的距离之和(总距离)尽可能小。
下面给出一个示例,假定你有 5 个客户,其办公楼都在一条街上,如下图所示。这 5 个办公楼分别位于距离大街起点 1km, 3km, 4km, 6km 和 12km 处。电信公司仅为你提供 K=2 条电缆。
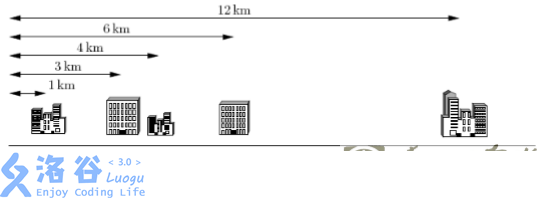
上例中最好的配对方案是将第 1 个和第 2 个办公楼相连,第 3 个和第 4 个办公楼相连。这样可按要求使用 K=2 条电缆。第 1 条电缆的长度是 3km―1km = 2km,第 2 条电缆的长度是 6km―4km = 2 km。这种配对方案需要总长 4km 的网络电缆,满足距离之和最小的要求。
<br/ >
解析
首先,容易想到最优解一定只能是相邻的办公楼两两连接构成的。理由很简单,任意的跨过某些办公楼连接的电缆一定不如只连接其跨过的任意两个相邻电缆。
那么,我们就只用分析如何处理相邻的两两办公楼之间连接电缆的问题,对于两两办公楼之间的距离,我们将其编号为(1sim n-1)。
我到这里是先想到一个dp,结果一看数据范围直接懵逼,(O(n^2))用脚趾头想都是过不了的。然后想了想似乎网络流也能做,不过复杂度貌似也过不去。。。
老夫掐指一算,(根据lyd的书)有了如下分析:
对于任意一对(相邻两个)办公楼(i,j),局部最优解只会有两种情况:
- 连接(i,j)。
- 连接(i-1,i)和(j,j+1)。
显而易见,1情况最优时(i-1,i)和(j,j+1)是不能选的。对于2情况,由于所有距离都是正数,故选择(i-1,i)和(j,j+1)两段一定比只选其中某一段更优。
但是我们发现如果直接贪心,也就是每次选择最小距离累加进答案,是有后效性的,因为这会导致最小距离两侧的距离不可选择,但最优解仍然有可能包含它们两个。
注意到此处直接贪心的后效性产生的原因仅仅是因为其影响了当前状态下最短距离两侧的距离的选择,既然如此,那我们不妨考虑一个可以反悔并消除之前选择的影响的贪心。
那么我们可以得到一种贪心:建立链表(1sim n-1),对应所有距离,并映射到一个优先队列中。每次贪心选择最短距离(k_d)累加进答案,假设其所在位置为(d),把(d-1,d+1)两段打上标记,表示不能选择,再在链表中删除(d-1,d,d+1)的节点,在堆中也删除对应的节点,再在链表原来的位置加入新节点,其权值为(k_{d-1}+k_{d+1}-k_{d})(k为距离大小),同时也在堆中新增一个权值为(k_{d-1}+k_{d+1}-k_{d})的节点。这样一来,当我们在之后的状态中再次选择新节点时,就会消除之前选择(d)的影响,相当于选择了(d-1,d+1)而不选(d)。
下图中,黑色填充表示选择该段。
第一次选择位置(d)的点时,答案(ans=cdots+k_d)。
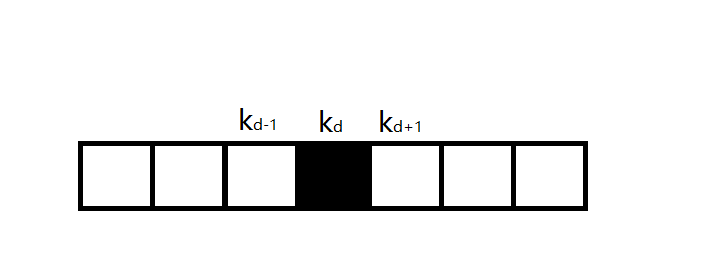
第二次选择该位置的点,答案(ans=cdots +k_d+k_{d-1}+k_{d+1}-k_{d}=cdots+k_{d-1}+k_{d+1})
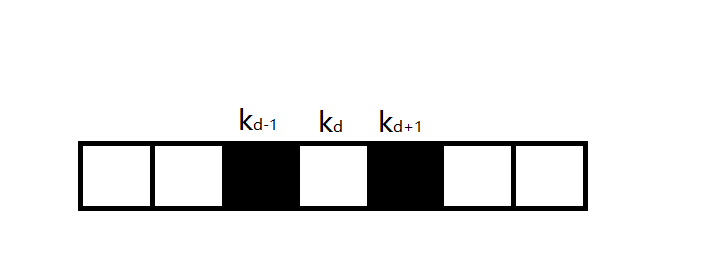
我们删除原节点并新增节点的操作实际上相当于对一个子问题做出了决策,并逐步解决规模更大的子问题。
下图中如果红框内表示当前状态的最优解,实际上他就是该子问题的最优解,在之后的决策中,我们可以直接使用这个子问题的最优解,而不用考虑其内部是如何构成的。
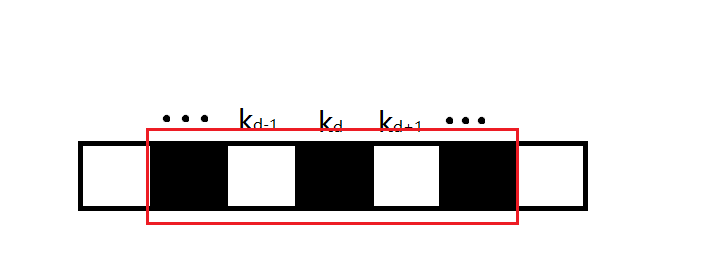
我们需要证明更一般的情况以解决整个问题,下面我们证明全局最优解也满足这个性质。
首先,显然我们的贪心具有决策包容性,任意的子问题一定包含了比它更小的所有子问题(这是一个区间上的问题)。
我们不妨使用微扰法和范围缩放法进行贪心正确性的证明。
尝试证明标记不可选择区域的操作的正确性,假设当前子问题状态如下:
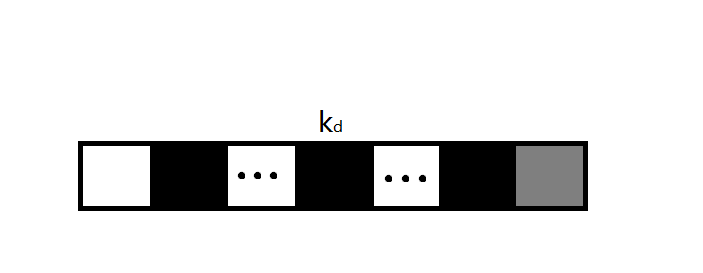
即,前一步时,子问题最优解为黑色区域,当前最短距离为灰色区域。如果此时我们选择了灰色区域,那么一定有所有距离(>)最右边的那段灰色距离,且已经选择的所有黑色区域的任意一个的距离(<)灰色区域的距离,因此在这个子问题中我们一旦选择了灰色区域,一定会减少一个比灰色区域更小的距离,增加一个比灰色区域更大的距离到答案中,这一定不是最优解。
显然这个性质可以扩展到任意子问题,即任意时刻做出如上贪心决策不会使得结果变差。
此外,我们还要注意一些细节:链表的上下界处理,我们要保证表头和表尾不被选择(它们不包含在任一子问题中),只需把初值赋为无穷大即可。
其它差不多的题:P1484 种树 P1792 [国家集训队]种树
参考代码
#include<cstdio>
#include<iostream>
#include<cmath>
#include<cstring>
#include<ctime>
#include<cstdlib>
#include<algorithm>
#include<queue>
#include<set>
#include<map>
#define N 500010
#define ll long long
#define INF 0x7fffffff
using namespace std;
inline ll read()
{
int f=1,x=0;char c=getchar();
while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}
return x*f;
}
struct node{
ll val;
int id;
bool operator<(const node &a)const{
return val>a.val;
}
node(){}
node(int _id,ll _val){id=_id,val=_val;}
};
ll a[N],n,k,sum[N];
bool v[N];
priority_queue<node> q;
struct link{
ll val;
int pre,next;
}g[N];
int main()
{
n=read(),k=read();
for(int i=1;i<=n;++i)
a[i]=read();
for(int i=1;i<n;++i){
g[i].pre=i-1,g[i].next=i+1;
sum[i]=a[i+1]-a[i];
g[i].val=sum[i];
q.push(node(i,sum[i]));
}
g[n].val=g[0].val=INF;
ll ans=0;
for(int i=1;i<=k;++i){
while(v[q.top().id]) q.pop();
node x=q.top();q.pop();ans+=g[x.id].val;
g[x.id].val=g[g[x.id].next].val+g[g[x.id].pre].val-g[x.id].val;
v[g[x.id].next]=v[g[x.id].pre]=1;
q.push(node(x.id,g[x.id].val));
g[x.id].next=g[g[x.id].next].next;
g[x.id].pre=g[g[x.id].pre].pre;
g[g[x.id].pre].next=x.id;
g[g[x.id].next].pre=x.id;
}
printf("%lld
",ans);
return 0;
}