窝当然不会ddp啦,要写这题当然是考虑优化裸dp啦,但是这题非常麻烦,于是变成了黑题。
首先,这个是没有上司的舞会模型,求图的带权最大独立集。
不考虑国王的限制条件,有
现在考虑限制条件,如果对每一个限制条件都做一次dp,复杂度达到(O(n^2)),无法承受。
显然,对于这些限制条件,每一次的变动不会影响其它大多数的状态。
对于一个限制条件,我们分开考虑,先考虑只对一个城市进行限制的情况。
若该城市被要求驻扎军队,那么如果在最优情况下它本来就需要军队,则没有影响;如果它本来不需要军队,由于此时所有子树都是最优解,那么它只会对从它到根节点的路径的最优解产生影响。
若该城市被要求不能驻扎,那么与上面的情况类似,如果它本来需要驻扎,那么会对它到根节点的路径造成影响。
综上所述,我们是否可以考虑对于每个限制条件,只对两个点到根节点之间的路径的某些状态进行修改呢?答案是肯定的。
假设待修改节点为(x)。首先,此时除了(xsim root)的路径上的节点所表示的状态,其它状态都是最优的。对于这条路径的更新,实际上就是又对这条路径做了一次dp,并强制(x)选或不选,从而限制转移。
显然这是可行的,但是复杂度仍为(O(n^2)),我们需要一些手段进行优化。
容易发现我们更新的是一条链,对于一条链,我们自然可以想到用倍增或者树剖(它们维护的都是树链)来处理每个点的转移。
以倍增为例。
首先考虑裸dp的步骤,一个一个跳,每次从儿子转移。那我们能不能一段一段地跳,每次从已有信息中转移呢?当然可以。
先考虑只有一个点的情况。
如果我们要对(x)进行限制,那么我们不妨把整个图变成这样,方便分析
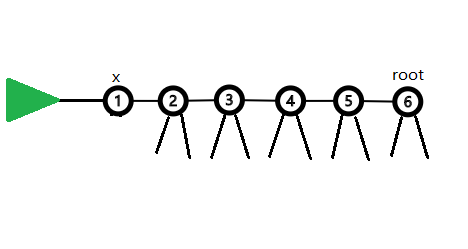
其中绿色的部分是(x)的子树的最优解。
显然我们在修改一个点之后,造成的对原最优解的影响是一定的,产生的新最优解是一定的,这意味着我们可以通过一些手段预处理出来。
不妨考虑通过倍增预处理出最优情况下每个点产生变动(选变成不选,不选变成选)在这条(xsim root)的链上产生的新最优解,也就是预处理出修改后dp时跳某一段的该段最优解。
然后从(x)树上倍增跳到(root),合并所得的新的最优解,就是这次限制条件下的答案。
实际上,我们的倍增预处理是在一次裸dp的基础上进行的。换句话说,倍增时用到的信息就是每个点表示的状态的原来的最优解,然后加一个限制条件,再做一个dp。
形象的讲,这个倍增预处理,就是dp套dp。
那这个倍增怎么做呢?
考虑状态的刻画,显然由几个较小的子问题合并成较大的子问题时,这些较小的子问题不能有交叉,否则无法基于二进制划分合并成更大的子问题。再者,子问题必须覆盖整个状态空间。也就是说,在状态定义时,我们要不重不漏。
既然如此,对于第一点,不难想到倍增时我们不仅要记录(x)的状态(0/1),还要记录它跳(2^k)步的祖先的状态。
对于第二点,不难想出状态包含的范围。
设(f[0/1][0/1][k][x])表示(x)节点变为0不可选、1可选时,向上(2^k)步的祖先(y)为0可选、1不可选时,(y)除去(x)以及(x)的子树的原最优解的其它所有子树的新最优解。
如下图,假设节点3是(x)的(2^k)祖先,状态为红色部分
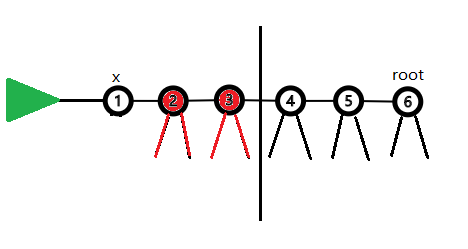
而3的(2^k)祖先(假设是(root))表示的状态就是蓝色部分。
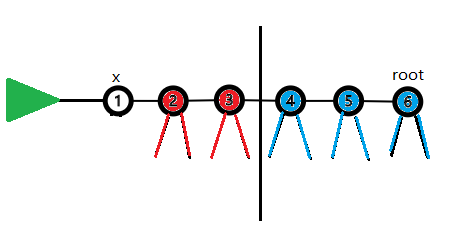
这样就可以很好的合并状态,之后统计答案的过程中,我们只需枚举(x)的状态并倍增跳即可。
对于节点(y),它的父节点为(x),有
得到转移(cao)
然后就是统计答案,当然是倍增统计答案。
从待修改点的两种不同状态开始往上倍增合并新最优解,直到根节点。
对于两个待修改点(x,y)的情况,我们像求LCA一样,先统计(xsim lca(x,y),ysim lca(x,y)),再统计(lca(x,y)sim root)即可。
注意一个细节,当(x,y)两点跳到(lca)的儿子处我们需要同时减去它们两个的原最优解,再往上跳。
复杂度降至(O(nlogn))。
树剖也是一个道理,预处理变动后最优解。
参考代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<string>
#include<cstdlib>
#include<queue>
#include<vector>
#define INF 0x3f3f3f3f
#define PI acos(-1.0)
#define N 100010
#define MOD 2520
#define E 1e-12
#define ll long long
using namespace std;
inline ll read()
{
ll f=1,x=0;char c=getchar();
while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}
return x*f;
}
struct rec{
int next,ver;
}g[N<<1];
int head[N],tot,n,m;
ll dp[2][N],f[2][2][21][N],gi[21][N],t,dep[N],w[N];
inline void add(int x,int y)
{
g[++tot].ver=y;
g[tot].next=head[x],head[x]=tot;
}
inline void dfs(int x,int fa)
{
dp[1][x]=w[x];dep[x]=dep[fa]+1;
f[0][0][0][x]=INF,gi[0][x]=fa;
for(int j=1;j<t;++j) gi[j][x]=gi[j-1][gi[j-1][x]];
for(int i=head[x];i;i=g[i].next){
int y=g[i].ver;
if(y==fa) continue;
dfs(y,x);
dp[0][x]+=dp[1][y];
dp[1][x]+=min(dp[1][y],dp[0][y]);
}
}
inline void init()
{
queue<ll> q;
q.push(1);
f[1][0][0][1]=dp[0][0]-dp[1][1];
f[0][1][0][1]=f[1][1][0][1]=dp[1][0]-min(dp[1][1],dp[0][1]);
while(q.size()){
ll x=q.front();q.pop();
for(int i=head[x];i;i=g[i].next){
int y=g[i].ver;
if(y==gi[0][x]) continue;
f[1][0][0][y]=dp[0][x]-dp[1][y];
f[0][1][0][y]=f[1][1][0][y]=dp[1][x]-min(dp[1][y],dp[0][y]);
for(int j=1;j<t;++j){
int fa=gi[j-1][y];
f[0][0][j][y]=min(f[0][0][j-1][y]+f[0][0][j-1][fa],f[0][1][j-1][y]+f[1][0][j-1][fa]);
f[0][1][j][y]=min(f[0][0][j-1][y]+f[0][1][j-1][fa],f[0][1][j-1][y]+f[1][1][j-1][fa]);
f[1][0][j][y]=min(f[1][0][j-1][y]+f[0][0][j-1][fa],f[1][1][j-1][y]+f[1][0][j-1][fa]);
f[1][1][j][y]=min(f[1][0][j-1][y]+f[0][1][j-1][fa],f[1][1][j-1][y]+f[1][1][j-1][fa]);
}
q.push(y);
}
}
}
inline ll get(ll x,int a,ll y,int b)
{
ll ans=0,lca;
if(dep[x]<dep[y]) swap(x,y),swap(a,b);
ll x0=INF,x1=INF,y0=INF,y1=INF,l0=INF,l1=INF;
a?x1=dp[1][x]:x0=dp[0][x],b?y1=dp[1][y]:y0=dp[0][y];
for(int j=t;j>=0;--j){
ll t0=x0,t1=x1;
if(dep[gi[j][x]]>=dep[y]){
x0=min(t0+f[0][0][j][x],t1+f[1][0][j][x]);
x1=min(t0+f[0][1][j][x],t1+f[1][1][j][x]);
x=gi[j][x];
}
}
if(x==y) lca=x,b?l1=x1:l0=x0;
else {
for(int j=t;j>=0;--j){
if(gi[j][x]!=gi[j][y]){
ll t0=x0,t1=x1,p0=y0,p1=y1;
x0=min(t0+f[0][0][j][x],t1+f[1][0][j][x]);
x1=min(t0+f[0][1][j][x],t1+f[1][1][j][x]);
y0=min(p0+f[0][0][j][y],p1+f[1][0][j][y]);
y1=min(p0+f[0][1][j][y],p1+f[1][1][j][y]);
x=gi[j][x],y=gi[j][y];
}
}
lca=gi[0][x];
l0=dp[0][lca]-dp[1][x]-dp[1][y]+x1+y1;
l1=dp[1][lca]-min(dp[0][x],dp[1][x])-min(dp[0][y],dp[1][y])+min(x1,x0)+min(y1,y0);
}
if(lca==1) ans=min(l0,l1);
else{
for(int j=t;j>=0;--j){
if(dep[gi[j][lca]]>1){
ll t0=l0,t1=l1;
l0=min(t0+f[0][0][j][lca],t1+f[1][0][j][lca]);
l1=min(t0+f[0][1][j][lca],t1+f[1][1][j][lca]);
lca=gi[j][lca];
}
}
ans=min(dp[0][1]-dp[1][lca]+l1,dp[1][1]-min(dp[0][lca],dp[1][lca])+min(l1,l0));
}
return ans<INF?ans:-1;
}
int main()
{
n=read(),m=read();
char op[5];
cin>>op;
t=log2(n)+1;
for(int i=1;i<=n;++i) w[i]=read();
for(int i=1;i<n;++i){
ll u=read(),v=read();
add(u,v),add(v,u);
}
dfs(1,0);
init();
while(m--){
ll x=read(),a=read(),y=read(),b=read();
if(a==0&&b==0&&(gi[0][x]==y||gi[0][y]==x)){
puts("-1");continue;
}
printf("%lld
",get(x,a,y,b));
}
return 0;
}