题目传送门
分析:
sb矩阵加速推一辈子。。。
想了1个小时,结果好像还和标准答案的方法不一样诶。。。
标算解法:
老套路,对于新加入的一列,考虑它与目前最后一列的关系
我们可以列出四种方案:
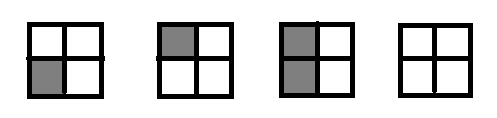
其中前两种我们知道一定使用了一个小块
但是后面两种就不知道是用过还是没用过了,用了就一定用了两个
所以再枚举两个状态0/1,表示用了或没用
然后就有了6个状态。。。
这6个状态可以互相胡乱转移一通,然后就可以得出答案2333
具体怎么转移其实不难,然后说一说自己的口胡写法2333
胡乱解法(自己的):
老套路,考虑新加入一行(假设两个碎块在前面已经用过)
此时考虑竖放和横放就是g ( i - 1 ) + g ( i - 2 )
然后考虑碎块放最后。。。
当确定两个碎块的间距后和相对位置时,摆放方式也就确定了
然后我们假设最后放的是包含碎块的几列,当列数为 j 时,前面的方案数就为Fib( i - j )
那么枚举 j 后的总方案就是SumFib ( i - 3 ) ,因为碎块长度最小为3
所以
g ( i ) = g ( i - 1 ) + g ( i - 2 ) + 2 * SumFib ( i - 3 )
前缀和我们推一下式子得到:
SumFib ( i ) = 2 * SumFib ( i - 1 ) - SumFib ( i - 3 )
然后这里有6个关键值,我们可以用5*5的矩阵维护

字很烂,原谅一下哈哈哈嗝。。。
然后矩阵加速就好了。。。

#include<cstdio> #include<cmath> #include<cstring> #include<algorithm> #include<queue> #define maxn 100005 #define MOD 1000000007 using namespace std; inline int getint() { int num=0,flag=1;char c; while((c=getchar())<'0'||c>'9')if(c=='-')flag=-1; while(c>='0'&&c<='9')num=num*10+c-48,c=getchar(); return num*flag; } struct node{ long long a[5][5]; friend node operator *(node x,node y) { node z;memset(z.a,0,sizeof z.a); for(int i=0;i<5;i++)for(int j=0;j<5;j++)for(int k=0;k<5;k++) (z.a[i][j]+=x.a[i][k]*y.a[k][j])%=MOD; return z; } }tr,I,A; int P[5][5]={{1,1,0,0,0},{1,0,0,0,0},{2,0,2,1,0},{0,0,0,0,1},{0,0,MOD-1,0,0}}; inline node ksm(node num,int k) { node ret=I; for(;k;k>>=1,num=num*num)if(k&1)ret=ret*num; return ret; } int main() { int T=getint(); for(int i=0;i<5;i++)I.a[i][i]=1; for(int i=0;i<5;i++)for(int j=0;j<5;j++)tr.a[i][j]=P[i][j]; A.a[0][0]=2,A.a[0][2]=2,A.a[0][3]=1; while(T--) { int n=getint()-3; if(n<0){printf("0 ");continue;} node tmp=A*ksm(tr,n); printf("%lld ",tmp.a[0][0]); } }

