Day 1 组合计数
1.组合数
（1）、C(n,m) 读作n选m，二项式系数 ：
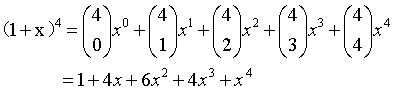
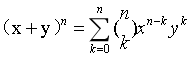
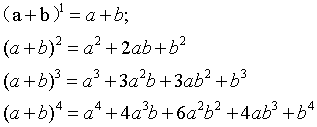
（2）、n个东西里选m个的方案数 不关心选的顺序:
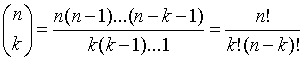
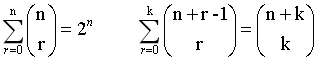
（3）、二项式系数--->多项式系数:
(x+y+z)^n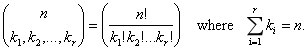 
2.组合数计算
（1）、递归、纯相加、带初始值的公式（递推：考虑选不选最后一个元素）：
（2）、初值（O(n^2)预处理）：
（3）、运算（复杂度O(n)）：
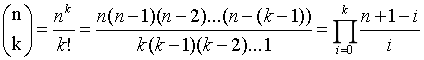
①可以保证每一步运算都是整数；
②保证单次O(n)计算组合数模任意数；
③可以记录组合数因子出现次数cnt(x)；
④若知道每个数x的最小质因子mnp(x)，从后往前扫 对于每个合数 将cnt(x/mnp(x))+=cnt(x) cnt(mnp(x))+=cnt(x)，最后可以得到质因数分解形式 由于质数个数O(n/ln(n)) 。
优化：(对于质数 可以O(n)预处理 O(1)求值 , N>INF, Lucas定理 注意模数必须是质数)
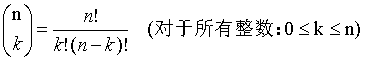
对于非负整数m, n和素数p，下面的同余关系成立:
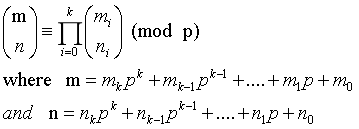
Ⅰ.如果模数也很大(n,m <= 1e9,P = 1e9+7)就分块打表，为了快速获得x!(x的阶乘)，设置B 打表B! (2B)! (3B)! …每次查询一个x!,只需要用表中最接近的值O(B)计算,表的长度O(P/B)
Ⅱ.如果模数不是定值，以后再说.......
3.组合数求前缀和
（1）、过程大致如下：
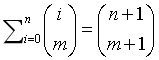
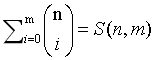
可以化简为：（S无法快速计算 但是可以递推）
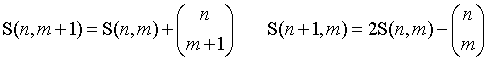
在多组询问的情况下可以使用莫队算法，也可以分块预处理出所有m是B的倍数的S
4.组合数组合意义
（1）、概念：
①共有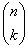
种方式从n元素中选取k项；
②共有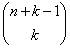
种方式从一个n元素中选取（容许重复选取）k元素建立多重集；
③共有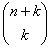
个字符串包含k个1和n个0；
④共有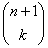
个字符串包含k个1和n个0，且没有两个1相邻；
⑤卡特兰数是：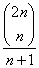
（2）、组合意义：
将n个可区分的元素放进r个可区分的容器里 第i个容器中放了k_i个的方案数
（3）、性质：
①一个没: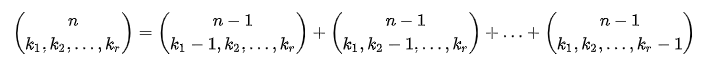
②对称性：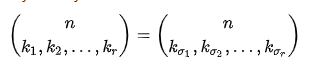
（4）、例题：
例1：一个网格纸 每次只能往右或往上走
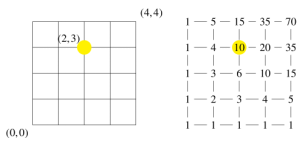
只向右或向上走的方案数为：C（n+m,m）或 C（n+m,n）;
证明：
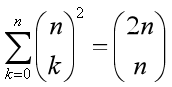
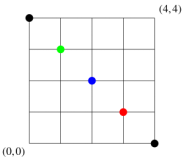
例2：
计算方程的整数解个数 一共有M个未知数要满足：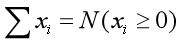
则：解的数量为C(N+M-1,M-1) (插板法).如果未知数有下限，直接将N减掉下限的和
5.组合数例题
例1：
一个正n边形 将其所有对角线连起来 一共有多少个交点（保证n是奇数 不存在三条对角线共点）。
∵4个点确定一个交点 ∴C(n,4) .
例2([AGC001E] BBQ Hard):
烧烤硬 问题陈述:
史努克正在举行另一场烧烤聚会。 这次，他要做一份烤串饭。他有一堆烤串饭盒。第i-th串肉套餐包含一个串，Ai片牛肉和Bi片青椒。这些包装里的所有串都是不同的，可以区分，而所有的牛肉片和青椒片，分别是不能区分的。为了做一顿串肉饭，他从他的串肉饭包里挑了两个，然后从选择的包里拿出所有的东西，也就是两个串和一些牛肉或青椒。(剩下的烤串套餐将不使用。)然后，所有的食物碎片都以任意顺序，一个一个地串在两根烤肉串上。
他可以用多少种不同的方法做一顿烤串饭?当且仅当所使用的串组不同或食物的顺序不同时，制作串餐的两种方法是不同的。因为这个数可以非常大，所以求它的模1e9+7。
问题简化：
给定a,b数组，要求下面式子模1000000007：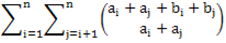
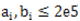
思路:
考虑把组合数描述成坐标。 那么这就是(−ai,−bi)到(aj,bj) ，中途只能向上或向左走的路径条数。 考虑在坐标系上点上所有点，直接来一波dp算方案:
f[i][j]=f[i][j]+f[i−1][j]+f[i][j−1];
如果本来就有一个点就初始化那个点为1。考虑这样算算重了自己的三象限坐标到自己一象限坐标的方案，所以要减去自己到自己的方案。 也就是说直接拿自己的组合数去减即可.
代码实现：
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<algorithm>
using namespace std;
typedef long long ll;
const int mod=1e9+7;
const int N=2e5+10;
const int M=2e3+10;
int n;
int a[N],b[N],f[M*2+1][M*2+1];
ll p[N],e[N],c[N];
ll ans;
inline int read() {
int n=0,f=1;char ch=getchar();
while (ch<'0' || ch>'9') {if(ch=='-') f=-1;ch=getchar();}
while (ch<='9' && ch>= '0') {n=(n<<3)+(n<<1)+ch-'0';ch=getchar();}
return n*f;
}
inline ll C(ll x,ll y) {
if(x<y) return 0;
if(x==y || !y) return 1;
return e[x]*c[y]%mod*c[x-y]%mod;
}
int main() {
n=read();
e[0]=p[1]=c[1]=c[0]=1,ans=0;
for(int i=1;i<=(M<<2)+100;++i) e[i]=e[i-1]*i%mod;
for(int i=2;i<=(M<<2)+100;++i) {
p[i]=(mod-(mod/i))*p[mod%i]%mod;
c[i]=c[i-1]*p[i]%mod;
}
for(int i=1;i<=n;++i) {
a[i]=read(),b[i]=read();
f[M-a[i]][M-b[i]]++;
ans=(ans-C(a[i]*2+b[i]*2,a[i]*2)%mod+mod)%mod;
}
for(int i=1;i<=(M<<1);++i) {
for(int j=1;j<=(M<<1);++j) {
f[i][j]=(f[i][j]+f[i-1][j])%mod;
f[i][j]=(f[i][j]+f[i][j-1])%mod;
}
}
for(int i=1;i<=n;++i) ans=(ans+f[a[i]+M][b[i]+M])%mod;
printf("%I64d\n",ans*p[2]%mod);
return 0;
}
/*
3
1 1
1 1
2 1
26
*/
例3:
问题描述：
给你一棵n个节点的有根树。你要给每个节点分配一个1~n的数字，使得每个节点分配的数字不同，并且每个节点分配的数字都是它子树内最小的，求方案数。
考虑树形dp，dp(i)表示i这个子树分配1~sz(i)的方案数,转移：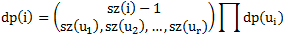
进一步推理可得：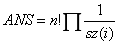
6.基础组合问题
（1）、基础概念：
①.加法原理 要么A 要么B A和B不相交,一个整数可以属于[1,3]或[4,6] 那么共有6种可能
②.乘法原理 AxB A和B中各选一个,第一个整数属于[1,3] 第二个整数属于[1,2] 共有6种可能.
③.n个可区分的元素选k个排成一列 排列方法有n(n-1)(n-2)…(n-k+1)=n!/(n-k)!种.
（2）、例题：
题目描述：
n个未知数，给定每个数的上限a_i，问你有多少种方法使得这些未知数都是正整数且互不相同。输出方案数模1e9+7。（n<=1e5 1<=a_i<=1e9 30）
思路：
考虑将a_i从小到大排序 依次确定未知数的值
ANS=a_1*(a_2-1)*(a_3-2)*…*(a_n-(n-1))
（3）、一个很有用的计数原则：
一个由计数对象组成的集合S，要计算它的大小|S|，考虑如果我们找到一个集合T，使得S的元素与T的元素一一对应，那么|S|=|T|
（4）、一个推广：
如果S的每个元素对应到a个T中的元素，T的每个元素对应到b个S中的元素，那么有：
a|S|=b|T| |S|=|T|*b/a
（5）、例题：
题目描述：
n个可区分的元素围成一排 有多少种方案？
思路：
S：n个元素的环排列 T：n个元素的排列
S->T：对于一个环排列 将其旋转 可以得到n个不同的排列 即对应到T中的n个元素
T->S：对于一个排列 只能被一个环排列旋转得到
n|S|=|T| |S|=|T|/n
7.Twelvefold way && 容斥原理
（1）、Twelvefold way 描述：
n个有标号/无标号的球分给m个有标号/无标号;盒子有三种限制：
A）无限制
B）每个盒子至少有一个球
C）每个盒子至多有一个球
共12种问题:
为了方便 将有标号记为L(labelled) 无标号记为U(unlabelled) 那么一个问题可以用缩写代替
（2）、Twelvefold way（①~⑦）
①(LLA)n个有标号的球分给m个有标号的盒子（m^n）
②(ULA)n个无标号的球分给m个有标号的盒子，等同于方程的整数解个数 C(n+m-1,m-1)
③(ULB)n个无标号的球分给m个有标号的盒子没有空盒，等同于方程整数解个数 C(n-1,m-1)
④(LLC)n个有标号的球分给m个有标号的盒子 每个盒子至多放一个球(m!/(m-n)!)
⑤(ULC)n个无标号的球分给m个有标号的盒子 每个盒子至多放一个球C(m,n)
⑥(LUC)n个有标号的球分给m个无标号的盒子 每个盒子至多放一个球[n<=m]
⑦(UUC) n个无标号的球分给m个无标号的盒子 每个盒子至多放一个球[n<=m]
（3）、容斥原理
①.基础：
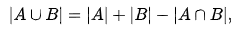
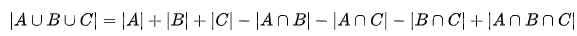
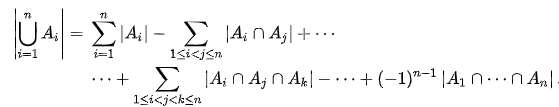
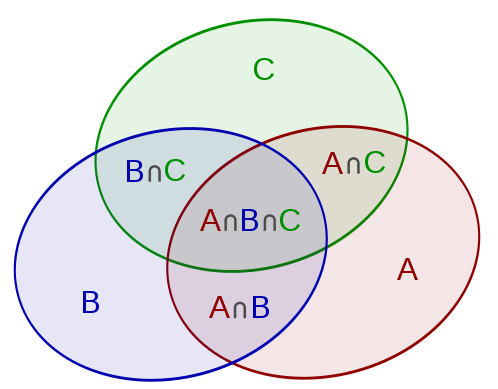
②.容斥原理基础应用(例题)：
1~100中既不被2整除也不被3整除也不被5整除的数有多少个？
A=被2整除的数的集合
B=被3整除的数的集合
C=被5整除的数的集合
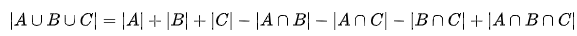
∴|A∪B∪C|=50+33+20-16-10-6+3=74 ∴100-74=26
（4）、Twelvefold way（⑧~⑨）
⑧(LLB)n个有标号的球划分给m个有标号的盒子 不能有空盒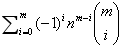
⑨(LUB) n个有标号的球划分给m个无标号的盒子 不能有空盒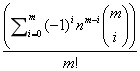 
8.Twelvefold way && 第二类斯特林数
（1）、第二类斯特林数简介：
就以（LUB）和（LLB）为例来简单说一下吧：
(LUB) 即n个有标号的球划分给m个无标号的盒子不能有空盒，(LLB) S(n,k)k!
（2）、递推式（考虑最后一个球是否独立给一个盒子）：
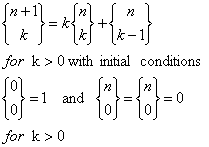
（3）、Twelvefold way （⑩）
(LUA)n个有标号的球划分给m个无标号的盒子，枚举有几个盒子被分配了
S(n,0)+S(n,1)+…+S(n,m)
9.Twelvefold way && 划分数
（1）、划分数(p(n,k))基础知识：
① n=x_1+x_2+…+x_k，将n划分为k个正整数的方案数 方案与x的顺序无关
② 递推式：p(n,k)=p(n-k,k)+p(n-1,k-1) （考虑最小的数是否为1）
（2）、Twelvefold way（最后两个）
11.(UUB)n个无标号的球划分给m个无标号的盒子 每个盒子至少有一个球 p(n,m)
12.(UUA)n个无标号的球划分给m个无标号的盒子，枚举有几个盒子被分配了，p(n,1)+p(n,2)+…+p(n,m) ，p(n+m,m).
（3）、Twelvefold way（完结篇）
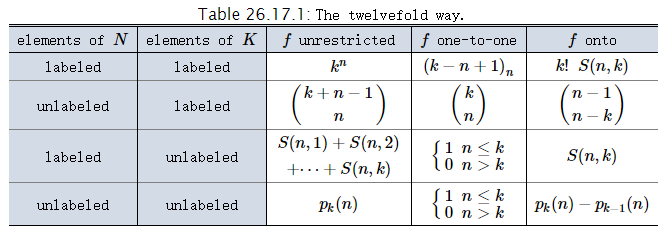
（PS：这里的p_k(n) 定义为至多划分为k个的划分数）
14.卡特兰数
（1）、基础：
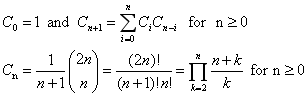
①.1,1,2,5,14,42,132,429,1430…
②.组合应用：
有2n个括号的合法括号序列个数(递推式相同)
如：C(3)=5 ((())) ()(()) ()()() (())() (()())
③.有n个非叶子节点的满二叉树的个数
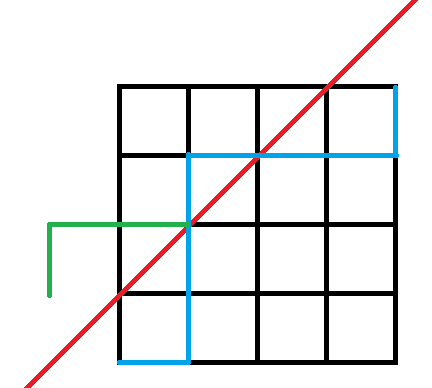
④.不超过对角线的NE 网格路径的个数(或算不经过y=x+1这条直线的路径个数)，具体来说，就是考虑碰到了这条直线的路径，我们将其之前的路径按照这条直线对称，那么可以对应到一个(-1,1)到(n,n)的路径， 又由于每个(-1,1)到(n,n)的路径都必然经过y=x+1这条直线，所以可以对应到一个(0,0)到(n,n)且碰到了y=x+1这条直线的路径；由之前提到的计数原则得到：(0,0)到(n,n)且碰到了y=x+1的路径条数与(-1,1)到(n,n)的路径条数相等，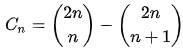
15.容斥原理进阶 && 容斥原理进阶练习
（1）、容斥原理可以与之前提到计数方法结合：
给定上界和下界的方程的整数解问题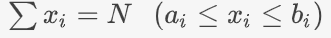
下界可以直接从N减掉,不满足X<=B X>=B+1,考虑容斥一个子集不满足上界后，所有变量只剩下界，可 以 直 接 组 合 数 计 算 方 案 数,由于最后方案数只和被减掉多少以及容斥系数有关，当未知数个数多但是上界小的时候，可以使用类似背包的动态规划优化.
（2）、例题：
例1：
题目描述：
问你有多少个n位数，满足以下要求：
1）这个数是回文串
2）奇数位的和等于偶数位的和
输出答案模1e9+7，n<=1e6
思路：
Ⅰ、位数是偶数 答案为10^(n/2)；
Ⅱ、位数是奇数：
解：设 abcdcba
则有：2a+2c=2b+d；
每个未知数的范围为[0,9].
移项后 得到：2x_1+2x_2+2x_3+….-2y_1-2y_2-2y_3-…-z=0
设有k1个正项 k2个负项
所有未知数的范围为[0,9]
首先z可以枚举
发现负项的取值范围为 [-9,0] 不妨将每个负项加9
这样式子就变成了
2x_1+2x_2+2x_3+…+2(9-y_1)+2(9-y_2)+…-z=18k2
此时除了z外所有未知数是等价的
问题就变成了 有k1+k2个值域在[0,9]的未知数 问他们的和为S有多少种方案
发现这是一个有上界的方程的整数解的问题
可以O(k1+k2)（即O(n)）枚举有几个数大于上界
最终复杂度O(10n)
例2：
题目描述：
给定n个障碍点(x_i,y_i) 求有多少条不经过障碍点的(0,0)到(X,Y)的NE 网格路径（n<=5000 0<=x_i,y_i,X,Y<=100000）。
思路：
dp(i)表示从(0,0)到(x_i,y_i)不经过除了终点外的障碍点的方案数
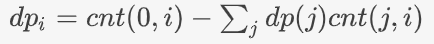
转移：枚举第一个碰到的障碍点将终点视为第n+1个障碍点 那么答案为dp(n+1)（PS：注意转移不会成环）
例3：
问题描述：
n种珠子，第i种有a_i个。将它们排成一列，要求相邻的两个珠子种类不同，问有多少种方案。
思路：
解：设S=a_1+a_2+…+a_n
原题条件：所有S-1对相邻的珠子种类不同难以直接容斥
转化：考虑某一种类的所有a_i个珠子 a_i-1对相对位置上相邻的珠子不相邻
对于某一种类 容斥后变为某些相对位置上相邻的珠子相邻 即这些珠子连成一段
不妨将这些珠子看做一个整体 那么我们可以把段数相同的情况合并 记录段数一定时 容斥系数的和记容斥后剩余x段的容斥系数的和为s_x
考虑如何计算对整体容斥的贡献
x段珠子与x个珠子在对排列方案数的贡献是相同的
每一类相当于变成：若看做1个珠子时 贡献系数为s_1 看做2个珠子时 贡献系数为s_2 …
总答案就是 枚举每类珠子被看做了几个珠子 计算排列成一列的方案数 将方案数乘上贡献系数s的积加入答案
可以使用类似背包的dp
例4：
问题描述：
n个不同的正整数排成一个序列，其中数字i出现次数为ci。对于每一个这样的序列，定义他的权值如下：
Ⅰ、将这个序列首尾相接放在一个圆上。把这些数字分成若干相邻的段，使得每段里都是在圆上相邻的数字，任意两段没有公共的元素，每一段中的数字都相同，相邻段中的数字不同。这个序列的权值定义为所有段的长度之积。求所有序列的权值和对1000000007取膜。（PS：虽然计算序列权值的时候是圆排列，但互为循环排列的不同序列仍然认为是不同的，如（1，2，1，2）和（2，1，2，1）就认为是不同的序列）
思路：
解：
先考虑序列上的问题，用之前介绍的方法做即可。
不同的是 我们不仅需要考虑容斥系数 还要考虑段的权值
可以使用dp计算出段数一定时 容斥系数乘权值的和 作为贡献系数
后面与之前介绍的方法完全一样
考虑如何处理环的问题
注意这题序列的开头与结尾如果数字相同 也视为同一段
可以考虑使用之前说的计数原则：
S：本题中描述的序列（代表一个环）包含d段数字1
T：一个开头为数字1，结尾不为数字1的序列 包含d段数字1
T->S：旋转n次，共对应到n个S中的元素
S->T：一共被d个T中的元素旋转到
所以得到n|T|=d|S| |S|=|T|*n/d
所以得到n|T|=d|S| |S|=|T|*n/d
由于我们计算的是T的集合里所有元素的代价和
并且S和T的对应关系并不会改变代价
所以我们只要算出所有T的元素的代价除以d（即数字1的段数）的和，再乘上n就可以得到S中所有元素的代价和，即最终答案
16.小练习（未完结...）
（1）、AGC018E
题目描述：
给定三个不相交的矩形A(X1,Y1)-(X2,Y2) B(X3,Y3)-(X4,Y4) C(X5,Y5)-(X6,Y6)，求有多少条NE lattice path从A中某个点出发 中途经过选定的B中的某个点 最终到达C中的某个点，ABC中选定的点不同 lattice path也视为不同（ 1<=X1<=X2<X3<=X4<X5<=X6<=1000000）.
（2）、某个题1：
题目描述：
飞机上有n个座位排成一列，共有m个乘客。你需要为每个乘客选定一个座位以及进入飞机的入口（要么从前门进 要么从后门进） 每个人会从指定的入口走向指定的座位，如果座位已经被占了，他就会继续向前走直到一个没有被占的座位，并占据那个座位。如果他直到飞机的一端都没有找到空座位，他就会生气。求有多少种分配的方案，使得没有人会生气。输出方案模1e9+7（n,m<=1e6）.
（3）、某个题2：
题目描述：
一共n+m个判断题，告诉你答案有n个YES m个NO。现在这n+m个题以随机的顺序依次给你，每道题你回答后就会告诉你答案是否正确。你使用最优策略回答问题。求期望你答对的题数。输出答案模1e9+7（n,m<=1e6）.