[Codeforces Round #433][Codeforces 853C/854E. Boredom]

题目链接：853C - Boredom/854E - Boredom

题目大意：在(n imes n)的方格中，每一行，每一列都恰有一个被标记的方格，称一个矩形为漂亮的当且仅当这个矩形有两个角是被标记的方格（这样的矩形有(frac{n(n-1)}{2})个）。给出(q)组询问，询问为一个二维区间，问有多少个漂亮的矩形与之相交。

题解：考虑每一个询问，将题中的方格分为如图所示9个区间

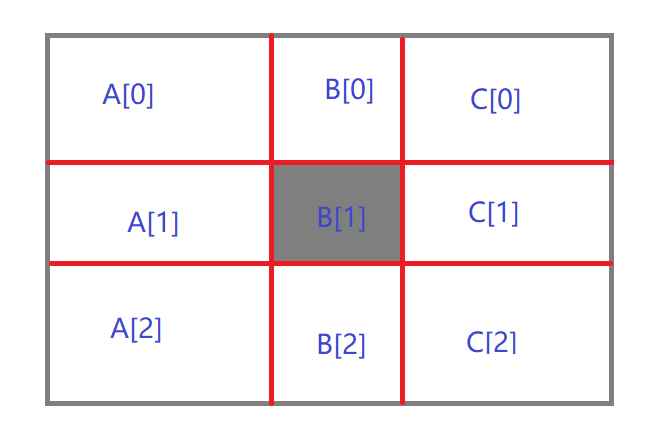
　　每个区间上的数字表示该区间内包含的被标记的点的个数，其中B[1]是询问的区域，为闭区间

　　将这些区间标记出来后，经过分类讨论即可得出答案

　　询问区间内点的个数可以通过二维树状数组来解决，但在这题里空间是肯定不够的，所以需要对询问离散化处理，然后离线做

#include<bits/stdc++.h>
using namespace std;
#define N 200001
struct rua{
    int l,u,r,d,id,a[3],b[3],c[3];
    void read(){scanf("%d%d%d%d",&l,&u,&r,&d);}
    long long get()
      {
      long long res=0;
      a[2]-=a[1],a[1]-=a[0];
      b[2]-=b[1],b[1]-=b[0];
      c[2]-=c[1],c[1]-=c[0];
      for(int i=0;i<3;i++)c[i]-=b[i],b[i]-=a[i];
      res+=1ll*a[0]*(b[1]+c[1]+b[2]+c[2]);
      res+=1ll*a[1]*(b[0]+c[0]+b[1]+c[1]+b[2]+c[2]);
      res+=1ll*a[2]*(b[0]+c[0]+b[1]+c[1]);
      res+=1ll*c[0]*(b[1]+b[2]);
      res+=1ll*c[1]*(b[0]+b[1]+b[2]);
      res+=1ll*c[2]*(b[0]+b[1]);
      res+=1ll*b[0]*(b[1]+b[2]);
      res+=1ll*b[2]*b[1];
      res+=1ll*b[1]*(b[1]-1)/2ll;
      return res;
      }
}q[N];
int n,m,p[N],t[N];
long long ans[N];
queue<int>Q;
int lowbit(int x){return x&(-x);}
bool cmp1(rua x,rua y){return x.l<y.l;}
bool cmp2(rua x,rua y){return x.r<y.r;}
void change(int x){while(x<N)t[x]++,x+=lowbit(x);}
int ask(int x){int res=0;while(x>0)res+=t[x],x-=lowbit(x);return res;}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
      scanf("%d",&p[i]);
    for(int i=1;i<=m;i++)
      q[i].read(),q[i].id=i;
    sort(q+1,q+m+1,cmp1);
    int cur=1;
    for(int i=1;i<=m;i++)
      {
      while(cur<q[i].l)change(p[cur]),cur++;
      q[i].a[0]=ask(q[i].u-1),
      q[i].a[1]=ask(q[i].d),
      q[i].a[2]=ask(N-1);
      }
    cur=0;
    sort(q+1,q+m+1,cmp2);
    memset(t,0,sizeof(t));
    for(int i=1;i<=m;i++)
      {
      while(cur<q[i].r)cur++,change(p[cur]);
      q[i].b[0]=ask(q[i].u-1),
      q[i].b[1]=ask(q[i].d),
      q[i].b[2]=ask(N-1);
      }
    for(int i=cur+1;i<=n;i++)change(p[i]);
    for(int i=1;i<=m;i++)
      q[i].c[0]=ask(q[i].u-1),
      q[i].c[1]=ask(q[i].d),
      q[i].c[2]=ask(N-1);
    for(int i=1;i<=m;i++)
      {
      int x=q[i].id;
      ans[x]+=q[i].get();
      }
    //for(int i=1;i<=m;i++)
      //for(int j=0;j<3;j++)
        //printf("%d %d %d
",q[i].a[j],q[i].b[j],q[i].c[j]);
    for(int i=1;i<=m;i++)
      printf("%I64d
",ans[i]);
}

在我的代码中，是先考虑了漂亮矩形的左边界在(l)左边的情况，然后加上整体在(l)的右边且右边界在(r)右边的漂亮矩形数，最后加上整体在([l,r])中的矩形个数