HDU

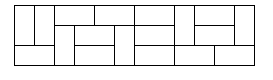
n how many ways can you tile a 3xn rectangle with 2x1 dominoes? Here is a sample tiling of a 3x12 rectangle.

Input
Input consists of several test cases followed by a line containing -1. Each test case is a line containing an integer 0 ≤ n ≤ 30.
Output
For each test case, output one integer number giving the number of possible tilings.
Sample Input
2
8
12
-1
Sample Output
3
153
2131

这道题的前身是若干个2×1的骨牌填满2×n。设当前填充长度为i，那么他只可能有下面两种情况：

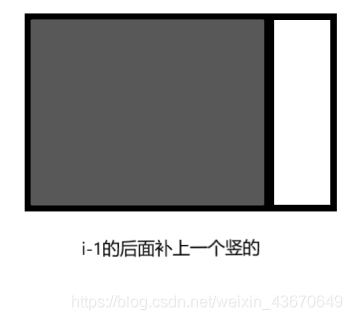
或者

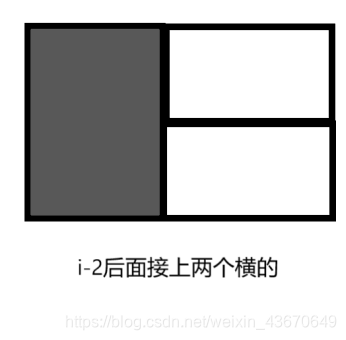
因此 f[i] = f[i-1] + f[i-2] ;

那么看 若干个2×1的骨牌填满3×n的情况，设当前填充长度为i，如果i为奇数必定无法填满（可以动手画）；如果i为偶数，那么i-2到i（长度为2的填法）有如下三种：

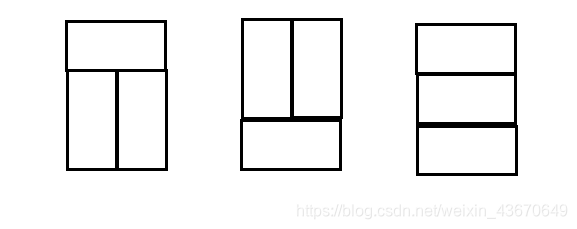
则 f[i]+=f[i-2]*3;（ f[i]初始为0 ）

上面是把 i 切割为 i - 2 和 2 的情况，那切割为 i - 4 和 4 呢？
便是这种情况 和 他的颠倒过来的情况。（共2种）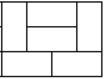
也许会产生疑问？？？
为什么没有下图的情况。

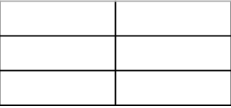
因为类似与之前的填充长度为二的情况我们已经考虑了
即 f[i] += f[i-2]* 3 => f[i-2] += f[i-4] * 3;
当为填充i-2的时候就已经算了三种，i 的时候又算三种，根据组合计数已经把类似于上图这种情况算进去了。
所以
f[i] += f[i-4] * 2;
同理

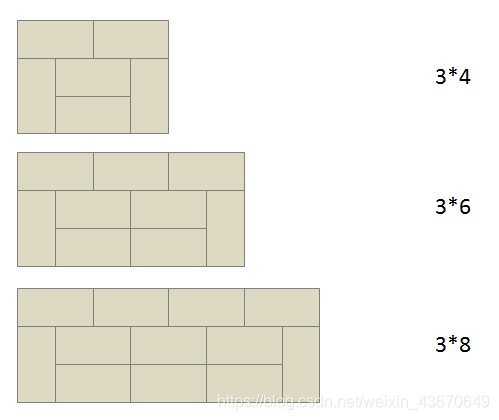
（该图片为百度搜得，若有雷同，还望口下留德 Orz ）
最终
f[n]= 3 * f[n-2] + 2 * f[n-4] + 2 * f[n-6] +…+ 2 * f [0];
由上式得出：
f[n-2] =3 * f[n-4] + 2 * f[n-6] + 2 * f[n-8]+…+ 2 * f[0];

化简得：f[n]=4*f[n-2]-f[n-4] ;

AC代码

#include<stdio.h>
#include<algorithm>
#include<math.h>
using namespace std;
typedef long long LL;
const int N=2e5+5;
int n;
LL f[35];
int main()
{
    f[0]=1; f[1]=0; f[2]=3;
    for(int i=3;i<=30;i++)
    {
        if(i&1) f[i]=0;
        else
            f[i]=f[i-2]*4-f[i-4];
    }
    while(scanf("%d",&n)==1&&n!=-1)
    {
        printf("%lld
",f[n] );
    }
    return 0;
}

另一种思路
f[i][0]=f[i-2][0]+f[i-1][1]+f[i-2][2];
f[i][1]=f[i-1][2];
f[i][2]=f[i][0]+f[i-1][1];
AC代码

#include<stdio.h>
#include<algorithm>
#include<math.h>
using namespace std;
typedef long long LL;
const int N=2e5+5;
int n,m;
LL f[35][3];
int main()
{
    f[0][0]=f[0][2]=1;
    for(int i=1;i<=30;i++)
    {
        if(i&1) f[i][0]=0;
        else
            f[i][0]=f[i-1][1]+f[i-2][2]+f[i-2][0];
        f[i][1]=f[i-1][2];
        f[i][2]=f[i][0]+f[i-1][1];
    }
    while(scanf("%d",&n)==1&&n!=-1)
    {
        printf("%lld
",f[n][0] );
    }
    return 0;
}

这种思路有点难理解，详见另一个大佬博客：
点此跳转