题目链接:传送门
题目思路:
显然,最长的偶权链的两个端点中,至少有一个是直径的端点。
简单证明一下,
若直径的权为偶,那么最长链肯定就是直径
若直径的权为奇,那么对于直径上任意一个点可以把直径分割为一段奇权链和一段偶权链。
那么可以使用反证法,假设最长的偶权链的两个端点都不是直径的端点。如下图所示:
首先明确一点:一个点在树上所能搜索出的最远的点一定是直径的端点(也可采用反证法证明)
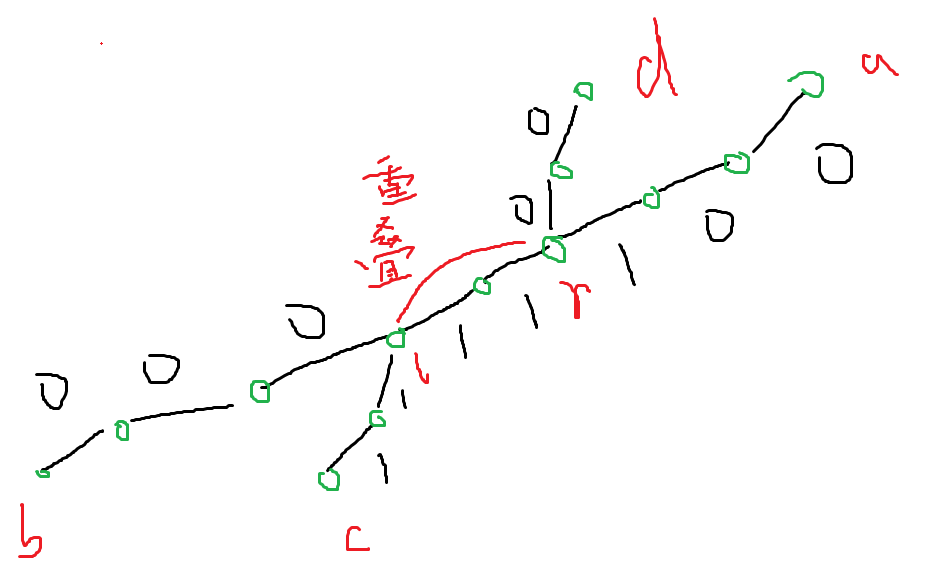
图中:ab是直径,cd是假定的答案(假定的最长偶权树链),lr是重叠部分;bl > cl , ra > rd (不满足的话c 或 d就是直径的端点了)
如果重叠部分lr为偶权,bl或ra为一偶一奇(按上图情况),那么cl和rd均为偶权,显然可以用bl去替换掉cl ,cd -> bd(按上图情况)
如果重叠部分lr为奇权,bl和ra均为偶权,那么cl和rd一个奇权 一个偶权,那么势必可以用bl 或者ar 对cl和rd中的偶权作替换;
证明完毕。
已知最长偶链端点一定是直径的某一端点,可以求出树的直径的两个端点,分别以这两个端点建树,用线段树维护其dfs序,每个点u维护的两个值,一个是根到u的奇权链长度,一个是根到u的偶权链长度,由于根到u的路径是唯一的,奇偶也是唯一的,所以偶权链或者奇权链的长度有一个为0,另一个则是u到根的距离。

1 #include<bits/stdc++.h> 2 /* 3 #include<cstdio> 4 #include<cmath> 5 #include<cstring> 6 #include<vector> 7 #include<cctype> 8 #include<queue> 9 #include<algorithm> 10 #include<map> 11 #include<set> 12 */ 13 //#pragma GCC optimize(2) 14 using namespace std; 15 typedef long long LL; 16 typedef unsigned long long uLL; 17 typedef pair<int,int> pii; 18 typedef pair<LL,LL> pLL; 19 typedef pair<double,double> pdd; 20 const int N=5e5+5; 21 const int M=8e5+5; 22 const int inf=0x3f3f3f3f; 23 const LL mod=1e8+7; 24 const double eps=1e-8; 25 const long double pi=acos(-1.0L); 26 #define ls (i<<1) 27 #define rs (i<<1|1) 28 #define fi first 29 #define se second 30 #define pb push_back 31 #define eb emplace_back 32 #define mk make_pair 33 #define mem(a,b) memset(a,b,sizeof(a)) 34 LL read() 35 { 36 LL x=0,t=1; 37 char ch; 38 while(!isdigit(ch=getchar())) if(ch=='-') t=-1; 39 while(isdigit(ch)){ x=10*x+ch-'0'; ch=getchar(); } 40 return x*t; 41 42 } 43 vector<pii> e[N]; 44 struct edge{int u,v,w;}a[N]; 45 int rt1,rt2,ma; 46 pii ma1[N],ma2[N]; 47 //建两颗树(一棵树需要c、lz、int、out、rk、deep数组;如果直接用数组名传参,参数表就太长了,不如直接做一个结构体) 48 struct node 49 { 50 int c[N<<2][2],lz[N<<2],in[N],out[N],rk[N],dep[N],col[N],tot; 51 inline void pushdown(int i) 52 { 53 swap(c[ls][0],c[ls][1]); 54 swap(c[rs][0],c[rs][1]); 55 lz[ls]^=1; lz[rs]^=1; 56 lz[i]=0; 57 } 58 inline void pushup(int i) 59 { 60 c[i][0]=max(c[ls][0],c[rs][0]); 61 c[i][1]=max(c[ls][1],c[rs][1]); 62 } 63 void build(int i,int l,int r) 64 { 65 c[i][0]=c[i][1]=lz[i]=0; 66 if(l==r) return (void)(c[i][col[rk[l]]]=dep[rk[l]]); 67 int mid=l+r>>1; 68 build(ls,l,mid); 69 build(rs,mid+1,r); 70 pushup(i); 71 } 72 void update(int i,int l,int r,int ll,int rr) 73 { 74 if(ll<=l&&r<=rr) return (void)(swap(c[i][0],c[i][1]),lz[i]^=1); 75 int mid=l+r>>1; 76 if(lz[i]) pushdown(i); 77 if(mid>=ll) update(ls,l,mid,ll,rr); 78 if(mid<rr) update(rs,mid+1,r,ll,rr); 79 pushup(i); 80 } 81 82 void dfs(int u,int pre) 83 { 84 in[u]=++tot; rk[tot]=u; 85 dep[u]=dep[pre]+1; 86 for(auto x:e[u]) 87 { 88 int v=x.fi,w=x.se; 89 if(v==pre) continue; 90 col[v]=col[u]^w; 91 dfs(v,u); 92 } 93 out[u]=tot; 94 } 95 }tr[2]; 96 void dfs2(int u,int pre) 97 { 98 ma1[u]=ma2[u]=mk(0,u); 99 for(auto x:e[u]) 100 { 101 int v=x.fi; 102 if(v==pre) continue; 103 dfs2(v,u); 104 pii t=ma1[v]; 105 if(t>ma1[u]) swap(t,ma1[u]); 106 if(t>ma2[u]) ma2[u]=t; 107 //f[u]=max(f[v],f[u]); 108 } 109 //printf("u = %d , fi = %d , se = %d ",u,ma1[u].fi,ma2[u].fi); 110 if(ma1[u].fi+ma2[u].fi>ma) ma=ma1[u].fi+ma2[u].fi,rt1=ma1[u].se,rt2=ma2[u].se; 111 ma1[u].fi++; ma2[u].fi++; 112 } 113 114 int main() 115 { 116 int n=read(); 117 for(int i=1;i<n;i++) 118 { 119 int x=read(),y=read(),z=read(); 120 a[i]=edge{x,y,z}; 121 e[x].eb(y,z); 122 e[y].eb(x,z); 123 } 124 dfs2(1,0); 125 // printf("%d %d ",rt1,rt2); 126 tr[0].dfs(rt1,0); 127 tr[0].build(1,1,n); 128 tr[1].dfs(rt2,0); 129 tr[1].build(1,1,n); 130 int m=read(); 131 for(int i=1;i<=m;i++) 132 { 133 int x=read(),y=a[x].u; 134 if(tr[0].dep[a[x].u]<tr[0].dep[a[x].v]) y=a[x].v; 135 tr[0].update(1,1,n,tr[0].in[y],tr[0].out[y]); 136 y=a[x].u; 137 if(tr[1].dep[a[x].u]<tr[1].dep[a[x].v]) y=a[x].v; 138 tr[1].update(1,1,n,tr[1].in[y],tr[1].out[y]); 139 printf("%d ",max(tr[0].c[1][0],tr[1].c[1][0])-1); 140 } 141 return 0; 142 }
每次翻转某一条边的权,实际上就是翻转整个子树所有点的权,对于单个点来说,就是奇权链变成偶权链,但是长度不变,只需要交换根到u 的奇权长度和偶权长度即可(延时标记处理)
代码:
