径向基神经网络简介
在上世纪 80 年代J.Moody 和 C.Darken 提出了神经网络结构模型,也被称作径向基函数网络,在这种结构模型中包含三层前馈神经网络。 这种神经网络结构的理论基础是:径向基是作为神经元的隐含基存在的,这些隐含基是构成隐含空间的主要元素,在隐含层可以改变输入的向量,这样就可以实现从低维度到高维度的转变,从而那些在低维度中不能解决的问题在高维度空间中便可以很容易的解决。
径向基函数网络在输入和输出上都具有不可比拟的优势,正是得益于这些优势,使得径向基函数在函数逼近、模式识别以及预测等领域得到广泛的应用。
径向基函数神经元模型
径向基函数网络是三层前馈神经网络,而其中负责接收外界信息的则是输入层,对于由空间层到隐含层的转换则是发生在隐含层,同时在隐含层还能实现非线性的转换。其第三层是起到输出的功能,是输入的最终结果。通过这种网络系统,信息就可以实现从空间层到隐含层,并且在隐含层发生非线性转变,最终以线性的形式传递到输出层。
在径向基函数中,函数是关于中心点对称的,而且对于远离中心点的神经元而言,他们表现出相当低的活性,所以他们随着距离的增加其活性会越来越低。径向基函数有多种形式,但是目前使用最普遍的形式是高斯函数。
如图 中所展示的是 RBF神经元模型,在这个模型中,|| dist||表示求取输入向量和权值向量的距离,神经元 radbas的输入为输入向量p和权值向量 w 的距离乘以阈值b ,斯函数 radbas 是典型的径向基函数,其表达式为:
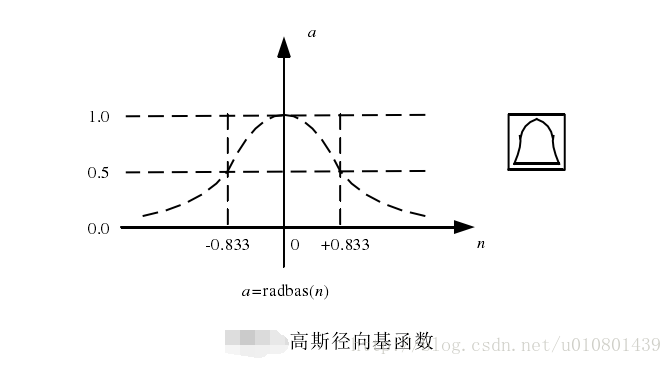
径向基函数的图形如图 所示,当 n =0 时,那么输出的结果最大为 1,同时随着权值向量 w 和输入向量 p 之间的距离缩小时,那么输出的结果就会变大。对此也可以这么解释,在径向基函数中,会在局部检测到输入信号,并作出响应。当输入信息出现在函数的中央区间时,将会在隐含层输出较高的值。所以说,网络能够表现出局部逼近的性能,因此也称
RBF 网络为局部感知场网络。而对于 RBF 神经元的灵敏度则可以通过阈值来调节,例如,假设神经元阈值为b =0.1,那么对于任意与权值向量 w 之间距离为 8.33 的输入向量 p ,其输出都是 0.5。
径向基函数还有很多不同的形式,常用径向基函数如表所示:
公式中的б称为基函数的扩展函数,影响函数的形状。б越小,基函数的选择性越大,函数逼近的越精确,但也存在适应过度的问题,反之б越大,则容易出误差较大的情况。