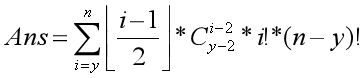【PKUWC2019模拟2019.1.15】Permutation

Description

Data Constraint

• 一个简单的计数。

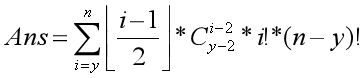
• 稍微化简一下发现我们需要求
• (i-1)/2*(i-2)!/(i-y)!
• 考场上的时候想到了这里，也想到了NTT，就是不会转换！！！？？
• 我们可以这样卷：
  • 设f[i]=(i-1)/2*(i-2)!,g[i]=1/(n-i)!
  • 那么那个式子就是
  • sigma(f[i]*g[j])[i+j==n+y]
  • 妙啊妙…
• 但这只是nlogn，还有O（n）的方法，然鹅nlogn也能勉强水过这题。。。

#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#define LL long long
#define maxn 2000005
#define mo 998244353
using namespace std;

int n,q,i,j,k,x,y,jc[maxn],ny[maxn];
int limit,a[maxn*2],b[maxn*2],bt[maxn*2];

LL ksm(LL x,LL y){
	LL s=1;
	for(;y;y/=2,x=x*x%mo) if (y&1) 
		s=s*x%mo;
	return s;
}

void ntt(int *a,int n,int sig){
	for(int i=0;i<n;i++) if (i<bt[i]) 
		swap(a[i],a[bt[i]]);
	for(int mid=1;mid<n;mid<<=1){
		int gn=ksm(3,(mo-1)/(mid<<1));
		if (sig<0) gn=ksm(gn,mo-2);
		for(int j=0;j<n;j+=(mid<<1)){
			int g=1;
			for(int k=0;k<mid;k++,g=(LL)g*gn%mo){
				int x=a[j+k],y=(LL)g*a[j+k+mid]%mo;
				a[j+k]=(x+y)%mo;
				a[j+k+mid]=(x-y+mo)%mo;
			}
		}
	}
}

int main(){
	freopen("permutation.in","r",stdin);
	freopen("permutation.out","w",stdout);
	scanf("%d%d",&n,&q);
	jc[0]=ny[0]=1;
	for(i=1;i<=n;i++) jc[i]=(LL)jc[i-1]*i%mo,ny[i]=(LL)ny[i-1]*ksm(i,mo-2)%mo;
	
	for(i=2;i<=n;i++) a[i]=(LL)(i-1)/2*jc[i-2]%mo,b[i]=ny[n-i];
	for(limit=1;limit<=n*2;limit<<=1);
	for(i=1;i<limit;i++) bt[i]=(bt[i>>1]>>1)|((i&1)?(limit>>1):0);
	ntt(a,limit,1),ntt(b,limit,1);
	for(i=0;i<limit;i++) a[i]=(LL)a[i]*b[i]%mo;
	ntt(a,limit,-1);
	int inv=ksm(limit,mo-2);
	for(i=0;i<limit;i++) a[i]=(LL)a[i]*inv%mo;
	
	for(i=1;i<=q;i++){
		scanf("%d%d",&x,&y);
		printf("%lld
",(LL)jc[n-y]*a[n+y]%mo);
	}
}