数据结构---图的邻接矩阵表示以及深度遍历

数据结构---图的邻接矩阵表示以及深度遍历

邻接矩阵表示

• 定义邻接矩阵的数据结构表示

  // 邻接矩阵
  typedef struct _graph
  {
  	char vexs[MAX];       // 顶点集合
  	int vexnum;           // 顶点数
  	int edgnum;           // 边数
  	int matrix[MAX][MAX]; // 邻接矩阵
  }Graph, *PGraph;
  

• 无向图的边的矩阵一定是一个对称矩阵，因为无向图只关心边是否存在，而不关心方向，V0和V1有边，那么V1和V0也有边。

• 找到每个点（ch）在邻接矩阵中的位置

  static int get_position(Graph g, char ch)
  {
      int i;
      for(i=0; i<g.vexnum; i++)
          if(g.vexs[i]==ch)
              return i;
      return -1;
  }
  

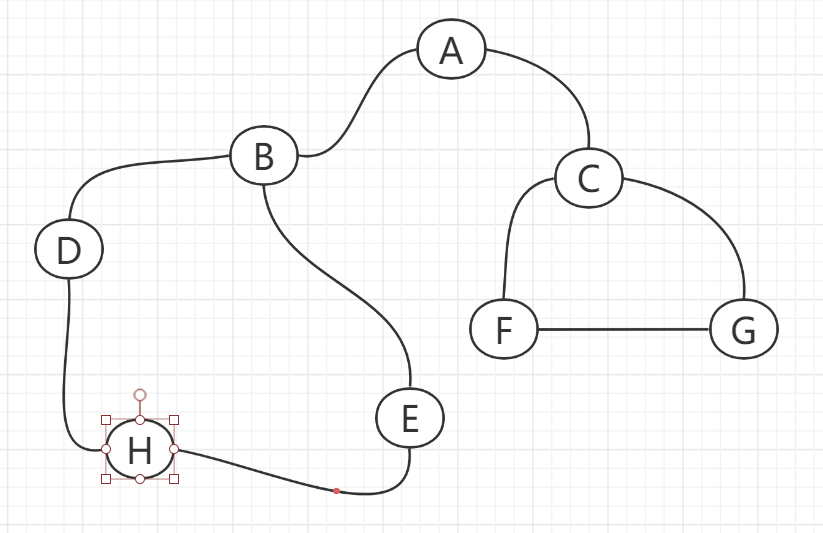
• 自定义一个图的连接方式 画出和中例子相同的图结构 用ABCDEFGH表示顶点

  

• 代码实现

  Graph* create_example_graph()
  {
  	char vexs[] = { 'A', 'B', 'C', 'D', 'E', 'F', 'G','H' };
  	char edges[][2] = {
  		{ 'A', 'B' },
  		{ 'A', 'C' },
  		{ 'B', 'D' },
  		{ 'B', 'E' },
  		{ 'C', 'F' },
  		{ 'C', 'G' },
  		{ 'D', 'H' },
          { 'E', 'H' },
          { 'F', 'G' }};
  	int vlen = LENGTH(vexs);
  	int elen = LENGTH(edges);
  	int i, p1, p2;
  	Graph* pG;
   
  	// 输入"顶点数"和"边数"
  	if ((pG = (Graph*)malloc(sizeof(Graph))) == NULL)
  		return NULL;
  	memset(pG, 0, sizeof(Graph));
   
  	// 初始化"顶点数"和"边数"
  	pG->vexnum = vlen;
  	pG->edgnum = elen;
  	// 初始化"顶点"
  	for (i = 0; i < pG->vexnum; i++)
  	{
  		pG->vexs[i] = vexs[i];
  	}
   
  	// 初始化"边"
  	for (i = 0; i < pG->edgnum; i++)
  	{
  		// 读取边的起始顶点和结束顶点
  		p1 = get_position(*pG, edges[i][0]);
  		p2 = get_position(*pG, edges[i][1]);
   
  		pG->matrix[p1][p2] = 1;
  		pG->matrix[p2][p1] = 1;
  	}
   
  	return pG;
  }
  

• 打印邻接矩阵

  void print_graph(Graph G)
  {
  	int i, j, k;
   
  	printf("Martix Graph:
  ");
  	for (i = 0; i < G.vexnum; i++)
  	{
  		for (j = 0; j < G.vexnum; j++)
  			printf("%d ", G.matrix[i][j]);
  		printf("
  ");
  	}
  }
  

深度遍历

• 图的深度优先搜索(Depth First Search)，和树的先序遍历比较类似。
• 假设初始状态是图中所有顶点均未被访问，则从某个顶点v出发，首先访问该顶点，然后依次从它的各个未被访问的邻接点出发深度优先搜索遍历图，直至图中所有和v有路径相通的顶点都被访问到。 若此时尚有其他顶点未被访问到，则另选一个未被访问的顶点作起始点，重复上述过程，直至图中所有顶点都被访问到为止。
• 深度优先搜索是一个递归的过程
• 过程对比书上的例子
• 代码实现

/*
 * 深度优先搜索遍历图
 */
void DFSTraverse(Graph G)
{
    int i;
    int visited[MAX];       // 顶点访问标记

    // 初始化所有顶点都没有被访问
    for (i = 0; i < G.vexnum; i++)
        visited[i] = 0;

    printf("DFS: ");
    for (i = 0; i < G.vexnum; i++)
    {
        //printf("
== LOOP(%d)
", i);
        if (!visited[i])
            DFS(G, i, visited);
    }
    printf("
");
}