定理.conjugate subgradient theorem
这个定理比较重要的一点在于指导如何求解对偶梯度,例如对于(y)存在(xinpartial f^*(y)),则(x)需要满足
[langle x,y
angle-f(x)=f^*(y)=max_{sup ilde{x}}(langle ilde x, y
angle-f( ilde x))
]
那么这时候我们只需要找到( ilde{x})即可求得对偶函数的梯度。
无约束条件下的算法
BB Algorithm
[egin{align}
x^{k+1}&=x^{k}-alpha_k
abla f(x^k)\
alpha_k&=frac{s_k^Ts_k}{s_k^Ty_k}
end{align}
]
where
[egin{align}
s^k&=x^k-x^{k-1}\
y_k&=
abla f(x^{k})-
abla f(x^{k-1})
end{align}
]
Proximal Point Method
[egin{align}
x^{k+1}&=argmin_{x}{f(x)+frac{1}{2alpha_k}Vert x-x^kVert}\
&= ext{prox}_{alpha_kf}(x^k)
end{align}
]
对 (x)进行求梯度
[x^{k+1}=x_k-alpha_k
abla f(x^{k+1})
]
Proximal Gradient Method
[min f(x)+g(x)
]
其中(f)凸光滑,(g)凸不光滑。对(f)函数进行展开逼近
[egin{align}x^{k+1}&=argmin_{x}f(x^k)+langle
abla f(x^k), x-x^k
angle+frac{1}{2alpha_k}Vert x-x^kVert +g(x)\
&= ext{prox}_{alpha_kg}(x^k-alpha_k
abla f(x^k))
end{align}
]
对偶视角
考虑一个线性凸约束问题
[egin{align}
min_x & f(x)\
ext{s.t.}&Ax=b
end{align}
]
构建Lagrange函数
[mathcal{L}(x, y)=f(x)+langle y, Ax-b
angle
]
令(d(y)=-min_{x}mathcal{L}(x, y)),则对偶问题为
[min_y d(y)
]
对偶梯度上升
利用梯度的方法得到
[y^{k+1}=y^k-alpha_kpartial d(y^k)
]
其中
[egin{align}
d(y)&=-min_xmathcal{L}(x,y)\
&=-min_x f(x)+y^TAx-y^Tb\
&=[-min_x -(-y^TAx-f(x)]+y^Tb\
&=f^*(-A^Ty)+y^Tb
end{align}
]
则
[egin{align}
partial d(y)=-A f^*(-A^Ty)+b label{eq:gradient of y}
end{align}
]
利用共轭函数的定理需求共轭函数的梯度,则此时的( ilde{x})需要满足
[egin{align} ilde{x}&=argmax_{ ilde{x}}{langle -A^Ty, ilde{x}
angle-f( ilde{x})}\
&=argmin_{ ilde{x}}{langle A^Ty, ilde{x}
angle+f( ilde{x})-y^Tb}\
&=argmin_xmathcal{L}(x, y)
end{align}
]
此时的更新方式为,也称对偶梯度上升
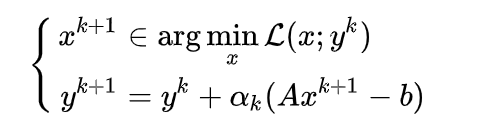
Dual Proximal point method
此时(y)的更新方式为
[y^{k+1}=y^{k}-alpha_kpartial d(y^{k+1})
]
由( ef{eq:gradient of y})可知
[egin{align}
partial d(y^k+1)&=-A partial f(-A^Ty^{k+1})+b\
&=-Aargmin_xmathcal{L}(x, y^{k+1})+b
end{align}
]
得(x^{k+1})为
[egin{align}
x^{k+1}&=argmin_x mathcal{L}(x, y^{k+1})\
&=argmin_x f(x)+langle y^{k+1}, A^Tx-b
angle\
&=argmin_x f(x)+langle y^k+alpha_k(A^Tx-b), A^Tx-b
angle\
&=argmin_x f(x)+langle y^k,(A^Tx-b)
angle +frac{alpha}{2}Vert A^Tx-b Vert^2\
end{align}
]
(x^{k+1})为增广拉格朗日,更新方式为
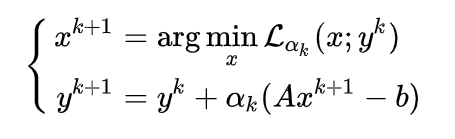
Dual Proximal Gradient Method
考虑问题
[egin{align}
min_x& f(x)+g(z)\
ext{s.t.}& Ax+Bz=b
end{align}
]
同样(f)凸光滑,(g)凸非光滑。Lagrange函数为
[mathcal{L}(x,z)=underbrace{f(x)+y^TAx}_{mathcal{L}_1(x, y)}+underbrace{g(z)+y^TBz-y^Tb}_{mathcal{L}_2(z,y)}
]
令(d_1(y)=-min_xmathcal{L}_1(x, y)),(d_2(y)=-min_zmathcal{L}_2(z,y))。对于对偶问题
[min_y d_1(y)+d_2(y)
]
利用Proximal Gradient Method更新(y)得到
[y^{k+1}= ext{prox}_{alpha_k d_2} (y^k-alpha_kpartial d_1(y^{k}))
]
令
[left{ egin{align} y^{k+1/2}&=y^k-alpha_kpartial d_1(y^k)& \
y^{k+1}&= ext{prox}_{alpha_k d_2}(y^{k+1/2})&end{align}
ight.
]
(y^{k+1/2})进行梯度下降,第二步进行proximal操作。其中
[partial d_1(y^{k})=-Ax^{k+1}
]
(x_{k+1}=argmin_x mathcal{L_1}(x, y))。第二步(y^{k+1})更新为
[egin{align}
y^{k+1} &= ext{prox}_{alpha_k d_2}(y^{k+1/2})\
&=y^{k+1/2}-alpha_k partial d_2(y^{k+1})
end{align}
]
(partial d_2(y^{k+1})=-Bz^{k+1}+b),而(z^{k+1}=argmin_z mathcal{L}_2(z,y^{k+1/2}))。最终的更新为
[left { egin{align} x^{k+1}&=argmin_x mathcal{L}_1(x, y^k)\
y^{k+1/2}&=y^{k}+alpha_kAx^{k+1}\
z^{k+1}&=argmin_z mathcal{L}_2(z,y^{k+1/2})\
y^{k+1}&=y^{k+1/2}+alpha_k(Bz^{k+1}-b)
end{align}
ight.
]
总结
我们只需要记住proximal操作是
[x^{k+1}=x^k-alpha
abla f(x^{k+1})
]
而对于有约束的问题我们需要求解对偶变量及其梯度。当求对偶变量梯度的时候使用共轭次梯度定理,满足定理条件的primal variable就是其当前次梯度。
[x=argmax_x{y^Tx-f(x)}
]
