2.4.5 堆排序
我们可以把任意优先队列变成一种排序方法。将所有元素插入一个查找最小元素的有限队列,然后再重复调用删除最小元素的操作来将他们按顺序删去。用无序数组实现的优先队列这么做相当于进行一次插入排序。用基于堆底优先队列这样做等同于哪种排序?一种全新的排序方法!我们就用堆来实现一种经典的排序算法——堆排序(Heap sort)。
堆排序可以分为两个阶段。在堆的构造阶段中,我们将原始数组重新组织安排进一个堆中;然后在下沉排序阶段,我们从堆中按递减顺序取出所有元素并得到排序结果。为了和我们已经学习过的代码保持一致,我们将使用一个面向大元素的优先队列并重复删除最大元素。为了排序的需要,我们不再将优先队列的具体表示隐藏,并将直接使用swim()和sink()操作。这样我们在排序时就可以将需要排序时就可以将需要排列的数组本身为堆,因此无需任何额外空间。
2.4.5.1 堆的构造
由N个给定的元素构造一个堆有多难?我们当然可以在与NlogN成正比的时间内完成这项任务,只需从左至右遍历数组,用swim()保证扫面指针左侧的所有元素已经是一棵堆有序的完全数即可,就像连续优先队列中插入元素一样。一个更聪明更高效的办法是从右至左用sink() 函数构造子堆。数组的每个位置都已经是一个子堆的根节点了,sink()对于这些子堆也适用。如果一个结点的两个子节点都已经是堆了,那么在该节点上调用sink()可以将它们变成一个堆。这个过程中会递归地建立起堆的只需。开始时我们只需要扫描数组中的一半元素,因为我们可以跳过大小为1的子堆。最后我们在位置1上调用sink()方法,扫描结束。在排序的第一阶段,堆的构造方法和我们的想象有所不同,因为我们的目标是构造一个堆有序的数组并使最大元素位于数组的开头(次大的元素在附近)而非构造函数结束的尾部。
命题R。用下沉操作由N个元素构造堆只需少于2N次比较以及少于N次交换。
证明。观察可知,构造过程中处理的堆都较小。例如,要构造一个127个元素的堆,我们会处理32个大小为3的堆,16个大小为7个堆,8个大小为15的堆,4个大小为31个堆,2个大小为63的堆和一个大小为127的堆,因此(最坏情况下)需要32*1+16*2+8*3+4*4+2*8+1*6= 120次交换(以及两倍的比较)。
1 /************************************************************************* 2 * Compilation: javac Heap.java 3 * Execution: java Heap < input.txt 4 * Dependencies: StdOut.java StdIn.java 5 * Data files: http://algs4.cs.princeton.edu/24pq/tiny.txt 6 * http://algs4.cs.princeton.edu/24pq/words3.txt 7 * 8 * Sorts a sequence of strings from standard input using heapsort. 9 * 10 * % more tiny.txt 11 * S O R T E X A M P L E 12 * 13 * % java Heap < tiny.txt 14 * A E E L M O P R S T X [ one string per line ] 15 * 16 * % more words3.txt 17 * bed bug dad yes zoo ... all bad yet 18 * 19 * % java Heap < words3.txt 20 * all bad bed bug dad ... yes yet zoo [ one string per line ] 21 * 22 *************************************************************************/ 23 24 /** 25 * The <tt>Heap</tt> class provides a static methods for heapsorting 26 * an array. 27 * <p> 28 * For additional documentation, see <a href="http://algs4.cs.princeton.edu/24pq">Section 2.4</a> of 29 * <i>Algorithms, 4th Edition</i> by Robert Sedgewick and Kevin Wayne. 30 * 31 * @author Robert Sedgewick 32 * @author Kevin Wayne 33 */ 34 public class Heap { 35 36 // This class should not be instantiated. 37 private Heap() { } 38 39 /** 40 * Rearranges the array in ascending order, using the natural order. 41 * @param pq the array to be sorted 42 */ 43 public static void sort(Comparable[] pq) { 44 int N = pq.length; 45 for (int k = N/2; k >= 1; k--) 46 sink(pq, k, N); 47 while (N > 1) { 48 exch(pq, 1, N--); 49 sink(pq, 1, N); 50 } 51 } 52 53 /*********************************************************************** 54 * Helper functions to restore the heap invariant. 55 **********************************************************************/ 56 57 private static void sink(Comparable[] pq, int k, int N) { 58 while (2*k <= N) { 59 int j = 2*k; 60 if (j < N && less(pq, j, j+1)) j++; 61 if (!less(pq, k, j)) break; 62 exch(pq, k, j); 63 k = j; 64 } 65 } 66 67 /*********************************************************************** 68 * Helper functions for comparisons and swaps. 69 * Indices are "off-by-one" to support 1-based indexing. 70 **********************************************************************/ 71 private static boolean less(Comparable[] pq, int i, int j) { 72 return pq[i-1].compareTo(pq[j-1]) < 0; 73 } 74 75 private static void exch(Object[] pq, int i, int j) { 76 Object swap = pq[i-1]; 77 pq[i-1] = pq[j-1]; 78 pq[j-1] = swap; 79 } 80 81 // is v < w ? 82 private static boolean less(Comparable v, Comparable w) { 83 return (v.compareTo(w) < 0); 84 } 85 86 87 /*********************************************************************** 88 * Check if array is sorted - useful for debugging 89 ***********************************************************************/ 90 private static boolean isSorted(Comparable[] a) { 91 for (int i = 1; i < a.length; i++) 92 if (less(a[i], a[i-1])) return false; 93 return true; 94 } 95 96 97 // print array to standard output 98 private static void show(Comparable[] a) { 99 for (int i = 0; i < a.length; i++) { 100 StdOut.println(a[i]); 101 } 102 } 103 104 /** 105 * Reads in a sequence of strings from standard input; heapsorts them; 106 * and prints them to standard output in ascending order. 107 */ 108 public static void main(String[] args) { 109 String[] a = StdIn.readAllStrings(); 110 Heap.sort(a); 111 show(a); 112 } 113 }
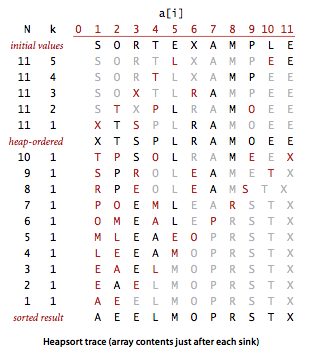
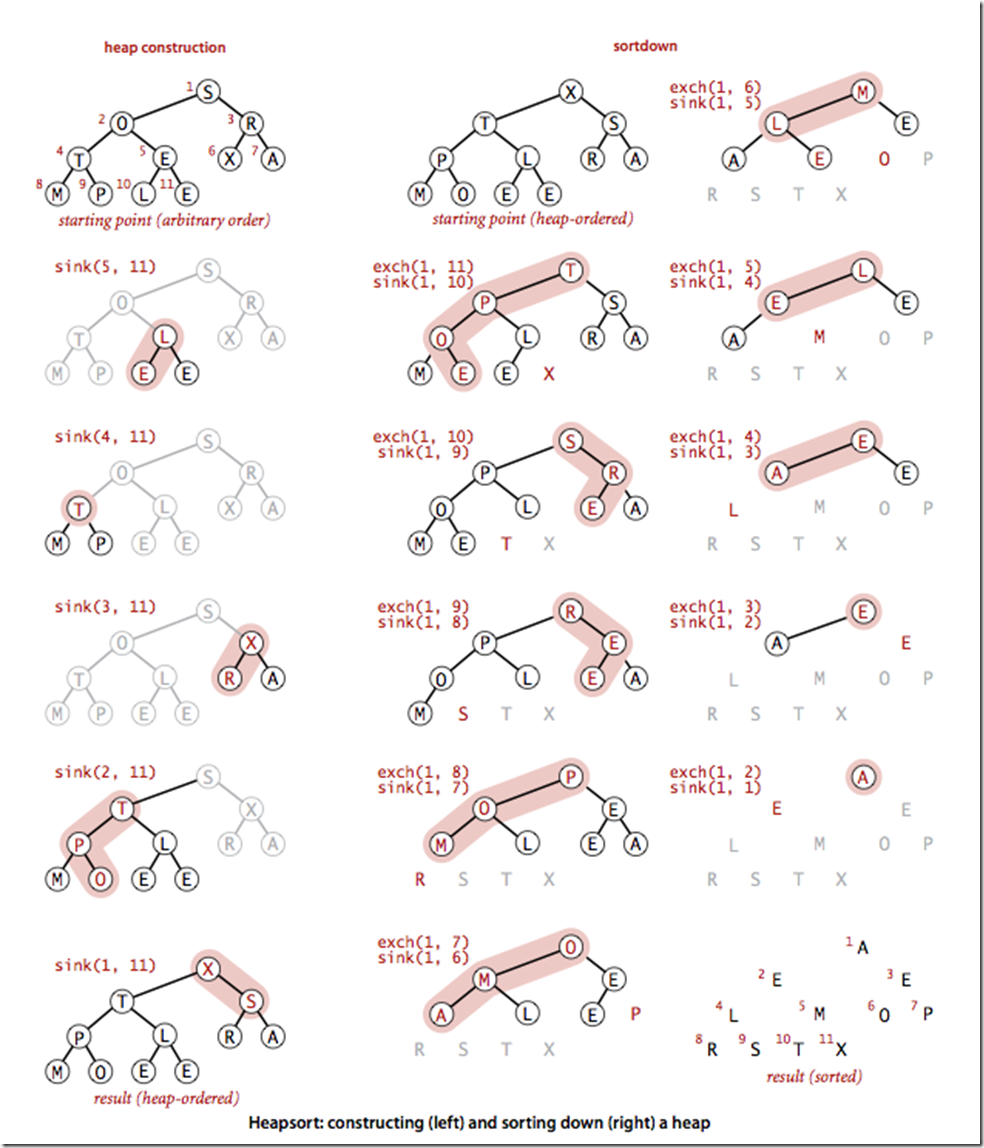
这 段代码用sink()方法将a[1]到a[N] 的元素排序(sink()被修改过,以a[]和N作为参数)。for循环构造了堆,然后while循环将最大的元素a[1]和a[N]交换并修复了堆,如 此重复直到堆变空。将exch()和less()的实现中的索引减一即可得到和其他排序算法一致的实现(将a[0]至a[N - 1]排序)。堆排序具体流程示意图如下显示。
2.4.5.2 下沉排序
堆排序的只要工作都是在第二个阶段完成的。这里我们将堆排序中的最大元素删除,然后放入堆缩小后数组中空出的位置。这个过程和选择排序有些类似(按照排序而非升序取出所有元素),但所需的比较要少的多,因为堆提供了一种从未排序部分找到最大的有效方法。
命题S。将N个元素排序,堆排序只少于(2NlgN + 2N)次比较(以及一半次数的交换)。
证明。2N项来自堆的构造(见命题R)。2NlgN项来自每次下沉操作最大可能需要2lgN次比较(见命题P 和命题Q )。
经典的堆排序算法,其发明者是J.W.J.Williams,并由R.W.Floyd 在1964年改进。尽管这段程序中虚幻的任务各不相同(第一段循环构造堆,第二段循环在下沉排序中销毁堆),他们都是基于sink()方法。我们将该实现和优先队列的API 独立开来是为了突出这个排序算法的简洁性(sort() 方法只需8行代码,sink()函数8行),并使其可以嵌入其他代码中。
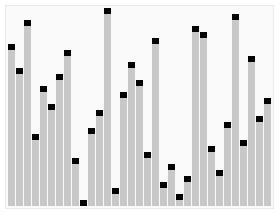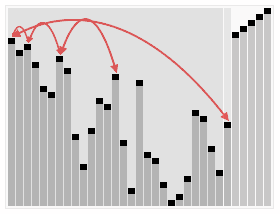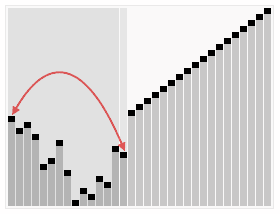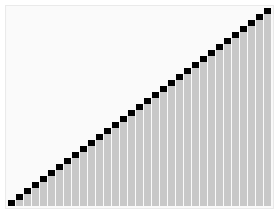
和以前一样,通过研究可视轨迹(如下图),我们可以深入了解算法的操作。一开始算法的行为似乎杂乱无章,因为随着堆的构造较大的元素都被移动到了数组的开头,但接下来算法的行为看起来就和选择排序一模一样了(除了比较次数更少以外)。
和我们许国的其他算法一样,很多人都研究过许多改进基于堆的有限队列的实现和堆排序的方法。我们这里简要地看看其中之一。
2.4.5.3 先下沉后上浮
大多数在下沉排序期间重新插入堆的元素会被直接加入到堆底,Floyd在1964年观察发现,我们正好可以通过免去检查元素是否到达正确位置来节省时间。在下沉中总是直接提升较大的子节点直至到达堆底,然后再使元素上浮到正确的位置。这个想法几乎可以将次数减少一半——接近了归并排序所需的比较次数(随机数组)。这种方法需要额外的空间,因此在实际应用中只有当比较操作代价较高时才有用(例如,当我们在将字符串或者其他键值较长类型的元素进行排序时)。
堆排序在排序复杂度的研究中有着重要的地位,因为它是我们所知的唯一能够同时最优地利用空间和时间的方法——在最坏的情况下它能保证使用 ~2NlgN次比较和恒定的额外空间。当空间十分紧张的时候(例如在嵌入式系统或低成本的移动设备中)它很流行,因为它只用几行就能实现(甚至机器码也是)很好的性能。但现在系统的许多应用很少使用它,因为它无法利用缓存。数组元素很少和相邻的其他元素进行比较,因此缓存未命中的次数要远远高于大多数比较都在相邻元素间进行的算法,如快速排序、归并排序,甚至是希尔排序。
另一方面,用堆排序的优先队列在现代应用程序中越来越重要,因为它能在插入操作和删除最大元素操作混合的动态场景中保证对数级别的运行时间。