#0.0 引入
我们这里有一张图

现在,我们需要把它存储到电脑中
输入格式:
第一行:n,m n表示点的数量,m表示边的数量
第2~m+1行: x,y,z 表示x到y的边的权值为z
本例输入为:
6 8
0 2 3
0 4 4
0 5 2
1 4 9
1 5 4
2 3 1
2 4 2
4 5 6
#1.0 邻接矩阵
邻接矩阵正如其名,实际便是一个二维数组,用于存储两点之间是否有边
我们定义一个数组M来存储
int M[101][101];
因为这个图有权值,我们需要先初始化这个数组(n为点的数量),当(M[i][j])的职为正无穷时,说明(i)与(j)之间没有边
void st(){
for (int i = 0;i < n ;i ++)
for (int j = 0;j < n;j ++)
M[i][j] = 0x7ffffff;
}
之后,(M)数组中变成了这样:
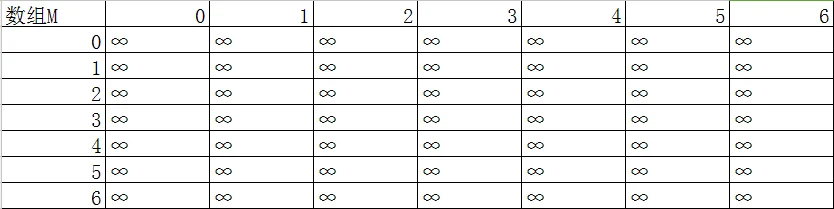
输入,不必多讲
void init(){
for (int i = 0;i < m;i ++){
int x,y,z;
cin >> x >> y >> z;
M[x][y] = z;
}
}
输入后,数组(M)变成了这个亚子:(标黄的为做出更改)
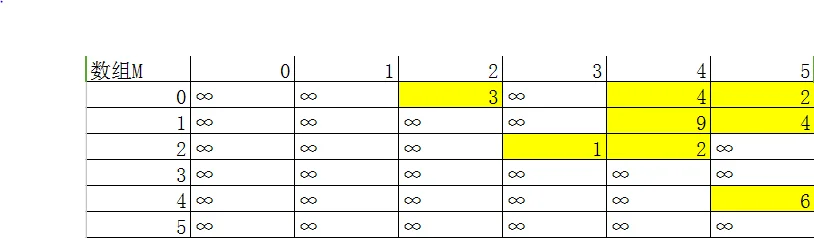
此时,这图便存储了进去。
邻接矩阵需要二维数组储存,数据过大时显然是无法使用的,因此,邻接矩阵并不常用
#2.0 邻接表
邻接矩阵在储存一个稀疏图时对于空间的浪费是极大的,那么我们可不可以只对边的数据进行储存?
就可以用到我们的一大杀器——邻接表
邻接表,存储方法跟树的孩子链表示法相类似,是一种顺序分配和链式分配相结合的存储结构。如这个表头结点所对应的顶点存在相邻顶点,则把相邻顶点依次存放于表头结点所指向的单向链表中。 --百度百科
#2.1 邻接表的存储
邻接表的实现方法有许多,这里只简单叙述常用的一种,其实下文的链式前向星也是邻接表的一种
首先,我们按照边读入的数据对边进行编号,如:
0 2 3这条边编号为(1);
2 3 1这条边编号为(6);
我们建立一个 Edge 类型的结构体,结构体定义如下:
struct Edge{
int u; //边的起点
int v; //边的终点
int w; //边的权值
};
Edge e[SIZE];
这样,例图的储存便是这样的:

我们现在已经将每一条边的数据存入了,但这样是不好遍历的,为了方便遍历,我们还需要将这些边连接起来
这里就要引出邻接表的精髓: next 数组和 first 数组
first[i]储存以i结点为起点的最后一条边(在输入顺序中)的编号, 一定要注意,这里储存的是编号next[j]存储与编号为j的边同起点的上一条边(在输入顺序中)的编号
分析上面的叙述,我们可以得到以下代码:
next[tot] = first[e[tot].u];
//之前以e[tot].u为起点的最后一条边在此次存储后变成了与tot号边同起点的上一条边
first[e[tot].u] = tot; //新的以e[tot].u为起点的最后一条边的编号为tot
tot ++; //增加边的编号
举个例子,例图中以 '0' 号结点为起点的边有

为了以后的遍历,录入前,我们要先将 first数组全部置为 (-1)
那么,当这些边全部录入后,first[0] 中储存的编号为 (3),而其中 next 数组存储情况则如下表:
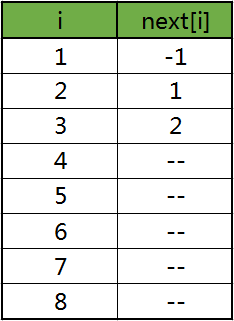
其他的边存储规则与之相同
存储完整代码:
inline void add(int u,int v,int w){
e[tot].u = u;
e[tot].v = v;
e[tot].w = w;
next[tot] = first[e[tot].u];
first[e[tot].u] = tot;
tot ++;
}
#2.2 邻接表的遍历
由上面的存储,我们可以看出,当我们想要遍历以 i 为起点的所有边时,只需要从 first[i] 中储存的边开始,依次查找 next[fisrt[i]],next[next[first[]i]]...当为 (-1) 时,说明没有下一条边了,可以停止,即为下面的程序:
inline void ergodic(){
for (int i = 0;i < n;i ++){
for (int j = first[i];j != -1;j = next[j])
...Do something you want...
}
}
通过观察可以发现,它遍历的顺序与输入的顺序恰好是相反的
完整储存与输出
#include <iostream>
#include <cstdio>
#include <cstring>
#define SIZE 100011
using namespace std;
struct Edge{
int u;
int v;
int w;
};
Edge e[SIZE];
int n,m,tot;
int first[SIZE],next[SIZE];
inline void add(int u,int v,int w){
e[tot].u = u;
e[tot].v = v;
e[tot].w = w;
next[tot] = first[e[tot].u];
first[e[tot].u] = tot;
tot ++;
}
inline void print(){
for (int i = 0;i < n;i ++){
printf("
%d:
",i);
for (int j = first[i];j != -1;j = next[j])
printf("%d -> %d w:%d
",i,e[j].v,e[j].w);
}
}
int main(){
memset(first,-1,sizeof(first));
scanf("%d%d",&n,&m);
for (int i = 0;i < m;i ++){
int u,v,w;
scanf("%d%d%d",&u,&v,&w);
add(u,v,w);
}
print();
return 0;
}
#3.0 链式前向星
还有一种常用的图的储存方式,链式前向星,(其实也是邻接表的一种)
#3.1 链式前向星的存储
学过上面的邻接表后,在看这就没什么难度了,因为储存方式基本相同
我们这样定义这个结构体:
struct Edge{
int w; \该边的权值
int to; \该边的终点
int next; \与这条边同起点的上一条边的编号
};
Edge e[SIZE];
我们还需要一个 head 数组,head 数组的定义如下:
head[i]储存以i结点为起点的最后一条边(在输入顺序中)的编号
这个 head 数组的定义是不是很眼熟?没错,它是我从上面粘贴过来的与上面邻接表 first 数组定义是相同的
这样看来,链式前向星不过是把上文邻接表的实现中的 next 数组移到了结构体中,所以我们可以轻松写出以下代码:
inline void add(int u,int v,int w){
e[tot].to = v;
e[tot].w = w;
e[tot].next = head[u];
head[u] = tot;
tot ++;
}
#3.2 链式前向星的遍历
与上文邻接表的遍历基本相同 =-= ,改动不大
inline void ergodic(){
for (int i = 0;i < n;i ++){
for (int j = head[i];j != -1;j = e[j].next)
...Do something you want...
}
}
#3.3 完整储存与输出
#include <iostream>
#include <cstdio>
#include <cstring>
#define SIZE 100011
using namespace std;
struct Edge{
int w; \该边的权值
int to; \该边的终点
int next; \与这条边同起点的上一条边的编号
};
Edge e[SIZE];
int n,m,tot;
int head[SIZE];
inline void add(int u,int v,int w){
e[tot].to = v;
e[tot].w = w;
e[tot].next = head[u];
head[u] = tot;
tot ++;
}
inline void print(){
for (int i = 0;i < n;i ++){
printf("
%d:
",i);
for (int j = head[i];j != -1;j = e[j].next)
printf("%d -> %d w:%d
",i,e[j].v,e[j].w);
}
}
int main(){
memset(first,-1,sizeof(first));
scanf("%d%d",&n,&m);
for (int i = 0;i < m;i ++){
int u,v,w;
scanf("%d%d%d",&u,&v,&w);
add(u,v,w);
}
print();
return 0;
}
更新日志及说明
更新
- 初次完成编辑 - (2020.10.16)
本文若有更改或补充会持续更新