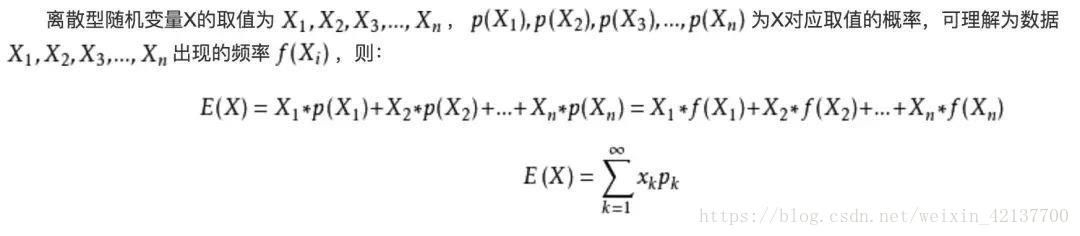https://blog.csdn.net/weixin_42137700/article/details/81664967
在学习的过程中,我经常会将频率和概率、均值和期望这两对概念搞混,这次总结一下,希望能对其他同学有所帮助。
1频率和概率
我们首先来看一个常见的误区。
当我们抛一门硬币50次的时候,出现20次正面朝上,30次反面朝下,我们有些同学会说,正面朝上的概率是2/5,这就是典型的将频率和概率没有区分出来。
在上面这个例子中,关于20次出现正面朝上,只能说正面朝上的频率是2/5,而不能说概率是多少多少。
因为概率是理想值,频率是实验值;例如抛理想均等硬币10000次正反面出现正面的频率是0.5+-$,其中$表示误差。
然而由大数定律可以证明当频率减去概率的模小于任意正数的时候可以认为在无穷多次实验中的频率值无限收敛于概率值。
我们首先给出概率的定义: 在一定条件下,重复做n次试验,nA为n次试验中事件A发生的次数,如果随着n逐渐增大,频率nA/n逐渐稳定在某一数值p附近,则数值p称为事件A在该条件下发生的概率,记做p(A)=p。这个定义成为概率的统计定义。
于是我们可以看出,概率其实是在无限次实验之后,频率的逼近值。而这个逼近过程是通过大数定理作为桥梁连接的。
2均值和期望
在初学的时候,我们经常也会将均值和期望搞混,实际上这两个量完全不是一个概念的。 均值 我们说的均值,其实是针对实验观察到的特征样本而言的。比如我们实验结果得出了x1,x2,x3.....xn这n个值,那么我们的均值计算是:
均值是观察样本的平均值,尽管随机变量一样,但是观察到的样本不同,那么我们就说他们的均值就是不同的,但是对于同一个随机变量来说,期望是唯一的,这就是他们的核心本质差别。
期望 但是期望是针对于随机变量而言的一个量,可以理解是一种站在“上帝视角”的值。针对于他的样本空间而言的。
如果说均值是一个统计量,那么期望是一种概率论概念,是一个数学特征。比如下面 首先给出公式:
例题,掷一枚六面骰子的期望值是3.5,计算如下: 1*1/6+2*1/6+3*1/6+4*1/6+5*1/6+6*1/6=3.5
均值和期望的联系也是大数定理联系起来的。随着重复次数接近无穷大,数值的算术平均值几乎肯定地收敛于期望值
3总结
说概率是频率随样本趋于无穷的极限
期望就是平均数随样本趋于无穷的极限