题目链接:http://poj.org/problem?id=2288
题目:
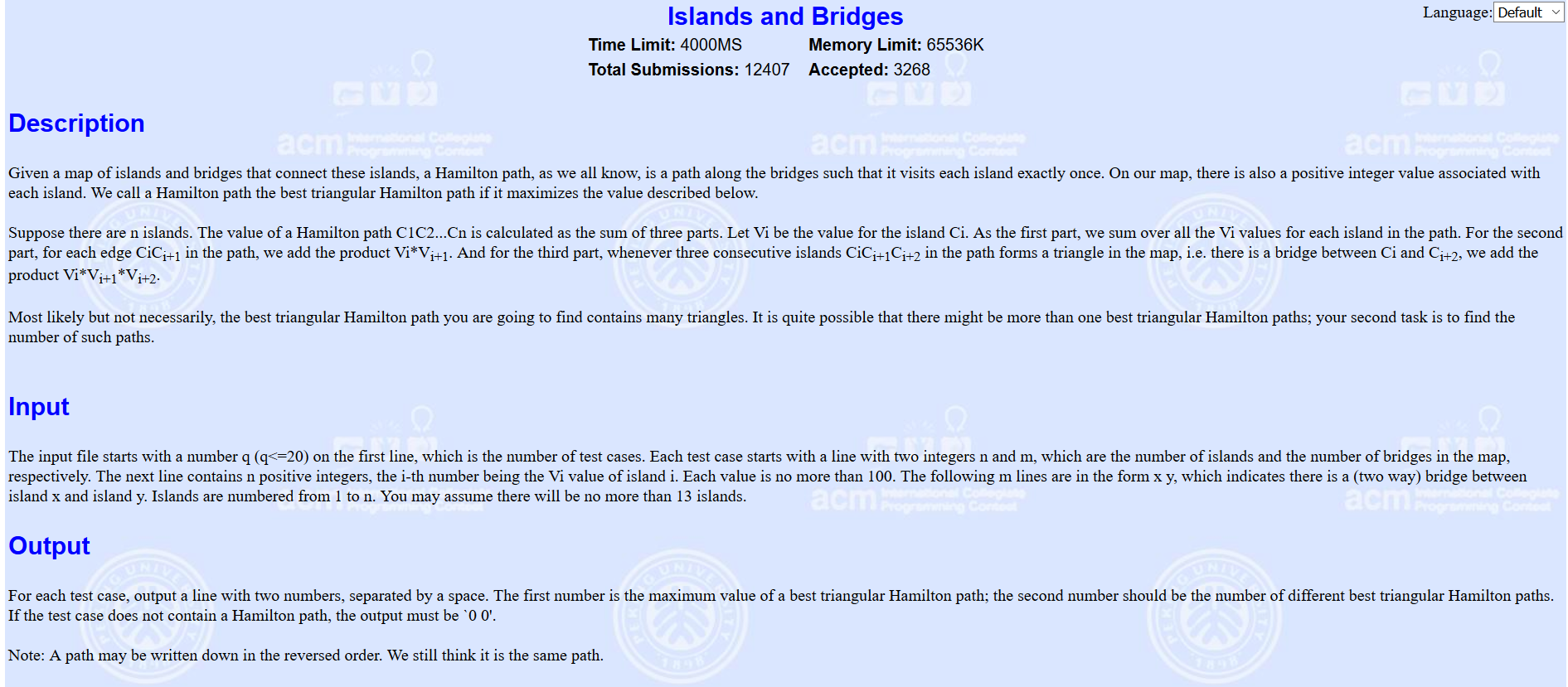

题意:求Hamilton 路径权值的最大值,且求出有多少条权值这么大的Hamilton路径。
思路:状压dp,dp[i][j][k]表示第i种状态下倒数第二个岛屿为j倒数第一个岛屿为k下的权值,cnt[i][j][k]记录条数。
当有边(i,j)存在时,有如下初值可赋:
d[(1<<i)+(1<<j)][i][j]=val[i]+val[j]+val[i]*val[j],cnt[(1<<i)+(1<<j)][i][j]=1。
如果状态(state,i,j)可达,检查岛k,如果此时k没有被访问过并且有边(j,k)存在,则做如下操作:
1)设tmp为下一步访问岛k时获得的总利益,r=state+(1<<k)。
2)如果tmp>d[r][j][k],表示此时可以更新到更优解,则更新:
d[r][j][k]=tmp,cnt[r][j][k]=cnt[state][i][j]。
3)如果tmp==d[r][j][k],表示此时可以获得达到局部最优解的更多方式,则更新:
cnt[r][j][k]+=cnt[state][i][j]。
最后检查所有的状态((1<<n)-1,i,j),叠加可以得到最优解的道路数。
需要注意的是,题目约定一条路径的两种行走方式算作一种,所以最终结果要除2。
代码实现如下:
1 #include <set> 2 #include <map> 3 #include <queue> 4 #include <stack> 5 #include <cmath> 6 #include <bitset> 7 #include <cstdio> 8 #include <string> 9 #include <vector> 10 #include <cstdlib> 11 #include <cstring> 12 #include <iostream> 13 #include <algorithm> 14 using namespace std; 15 16 typedef long long ll; 17 typedef pair<ll, ll> pll; 18 typedef pair<ll, int> pli; 19 typedef pair<int, ll> pil;; 20 typedef pair<int, int> pii; 21 typedef unsigned long long ull; 22 23 #define lson i<<1 24 #define rson i<<1|1 25 #define bug printf("********* "); 26 #define FIN freopen("D://code//in.txt", "r", stdin); 27 #define debug(x) cout<<"["<<x<<"]" <<endl; 28 #define IO ios::sync_with_stdio(false),cin.tie(0); 29 30 const double eps = 1e-8; 31 const int mod = 10007; 32 const int maxn = (1<<13) + 7; 33 const double pi = acos(-1); 34 const int inf = 0x3f3f3f3f; 35 const ll INF = 0x3f3f3f3f3f3f3f; 36 37 int t, n, m, u, v; 38 int w[13], mp[15][15]; 39 ll dp[maxn][13][13], cnt[maxn][15][15]; 40 41 int main() { 42 //FIN; 43 scanf("%d", &t); 44 while(t--) { 45 memset(mp, 0, sizeof(mp)); 46 memset(dp, -1, sizeof(dp)); 47 memset(cnt, 0, sizeof(cnt)); 48 scanf("%d%d", &n, &m); 49 for(int i = 1; i <= n; ++i) { 50 scanf("%d", &w[i]); 51 } 52 for(int i = 1; i <= m; ++i) { 53 scanf("%d%d", &u, &v); 54 mp[u][v] = mp[v][u] = 1; 55 } 56 if(n == 1) { 57 printf("%d 1 ", w[1]); 58 continue; 59 } 60 for(int i = 1; i <= n; ++i) { 61 for(int j = 1; j <= n; ++j) { 62 if(i != j && mp[i][j]) { 63 dp[(1<<(i-1))|(1<<(j-1))][i][j] = w[i] + w[j] + (ll) w[i] * w[j]; 64 cnt[(1<<(i-1))|(1<<(j-1))][i][j] = 1; 65 } 66 } 67 } 68 int tot = 1 << n; 69 for(int i = 0; i < tot; ++i) { 70 for(int j = 1; j <= n; ++j) { 71 if(i & (1<<(j-1))) { 72 for(int k = 1; k <= n; ++k) { 73 if(j != k && (i & (1<<(k-1))) && mp[j][k] && dp[i][j][k] != -1) { 74 for(int x = 1; x <= n; ++x) { 75 if(j != x && k != x && mp[k][x] && (i & (1<<(x-1))) == 0) { 76 ll tmp = dp[i][j][k] + w[x] + (ll)w[k] * w[x]; 77 if(mp[j][x]) tmp += (ll)w[k] * w[j] * w[x]; 78 if(tmp > dp[i|(1<<(x-1))][k][x]) { 79 dp[i|(1<<(x-1))][k][x] = tmp; 80 cnt[i|(1<<(x-1))][k][x] = cnt[i][j][k]; 81 } else if(tmp == dp[i|(1<<(x-1))][k][x]){ 82 cnt[i|(1<<(x-1))][k][x] += cnt[i][j][k]; 83 } 84 } 85 } 86 } 87 } 88 } 89 } 90 } 91 ll ans1 = 0, ans2 = 0; 92 for(int i = 1; i <= n; ++i) { 93 for(int j = 1; j <= n; ++j) { 94 if(i == j) continue; 95 if(dp[tot-1][i][j] > ans1) { 96 ans1 = dp[tot-1][i][j]; 97 ans2 = cnt[tot-1][i][j]; 98 } else if(dp[tot-1][i][j] == ans1) { 99 ans2 += cnt[tot-1][i][j]; 100 } 101 } 102 } 103 printf("%lld %lld ", ans1, ans2 / 2); 104 } 105 return 0; 106 }