更新于20180823
时序检查中对异步复位电路的时序分析叫做()和()?
这个题做的让人有点懵,我知道异步复位电路一般需要做异步复位、同步释放处理,但不知道这里问的啥意思。这里指的是恢复时间检查和移除时间检查。
在开始之前需要先搞明白的一点是为什么要保持建立时间和保持时间大于零,不满足的话会怎么样呢?
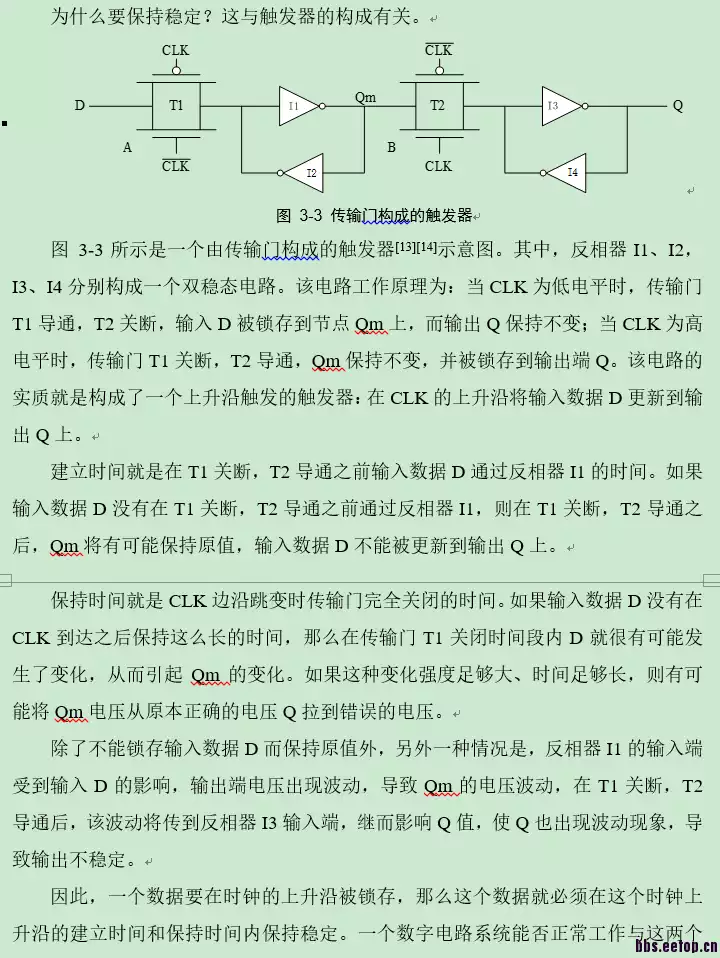
首先需要明白的一点就是D触发器的构造,D触发器实际上是由一个传输门加上反相器组成的双稳态电路组成的如下图:
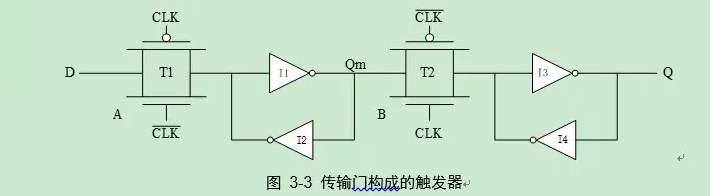
这个电路的工作情况:clk为低电平的时候传输门T1导通,T2关断,输入数据D会被锁存到Qm处。然后在clk为高电平的时候,T1关断,T2导通,输入数据Qm传输到Q上面去。这个过程实际上就是在时钟上升沿的时候将D数据 转移到Q上面去。
建立时间指的是在T1导通T2关断的时候,输入数据D到达Qm所用的时间,假设这个时候D没有到达Qm,会导致其输出的是原先的值,或者是错误的值,保持时间指的是在T1关断,T2导通的时候,Qm 到达Q用的时间,假设输入D没有在sclk到达后保持这么长的时间的话,加入变化的快的话,D变化导致的Qm变化从而使得输出的Q采集到不正确的值,这也是亚稳态的一种吧。还有一种情况就是反相器的I1 的输入端因为D输入变化而使得Qm电压波动,这个波动会在T2导通后传输到Q端
一、时序分析
首先需要明确的是深入理解什么是建立时间,什么是保持时间,还是用图来说话
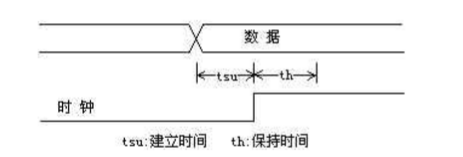
Tsu:保证数据在时钟采样是是稳定的,决定了该触发器之间组合逻辑的最大延迟
Th:保证数据能准确的被采样,决定了该触发器之间组合逻辑的最小延迟
在实际上做时序分析的时候可以分两类分别分析
1.组合逻辑的时序分析:电路上的延时是加性的
2.时序逻辑的时序分析:电路上的延时是非加性的
一个典型的模型在实际电路中,通常是时序逻辑和组合逻辑的结合,保证两种电路之间的数据传输没有问题的关键是要保证满足建立时间和保持时间之间的关系。,也就是说对于D2而言,它的建立时间和保持时间与D1的建立保持时间无关,只取决于D2的组合逻辑延时以及D1 的传输延时。
例题:假设第一个触发器的D1的建立时间最大值为T1max,最小为T1min,组合逻辑的延时最大为T2max,最小为T2min,请问第二个触发器D2的建立时间和保持时间瞒住的关系。
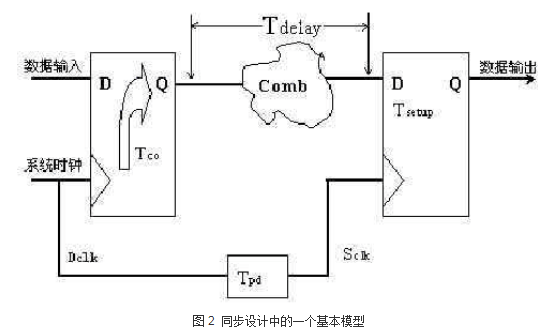
图中tco指的是触发器从0翻转到1所用的时间,有的地方叫tdq
Tdelay指的是组合逻辑的延时,tpd是时钟传输的延时,但实际上在FPGA中这部分的延时已经做到了很小了完全可以忽略掉的,有的地方叫tskew
进入正题开始分析:用时序电路图的方法,先假设tpd为零
对于D2的建立时间可以画图:
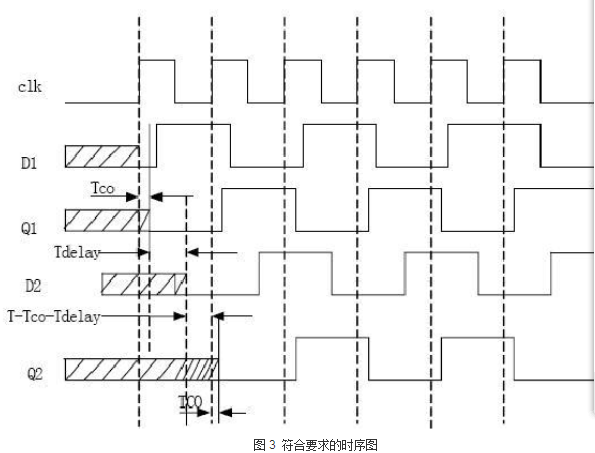
建立时间满足公式:Tco+Tdelay+T3<T T3<T-Tco-Tdelay 那么这里的Tco和Tdelay应该取max
保持时间与建立时间满足公式Th+Tsetup=Tclk,因此,可以得到T4<Tco+Tdelay这里取min
把时钟延时加上,即Tpd!=0时,有如下时序图:
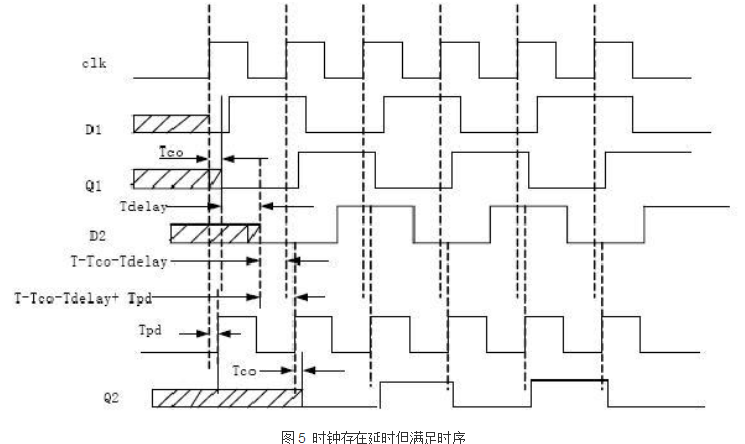
可以计算的到,建立时间放宽了Tpd,为Tclk+Tpd-(Tco+Tdelay)>=T3,Th减小为Tco+T2min-Tpd。
总结:
简易公式:
以下两个公式确定了D2的Tsetup和Thold:
1) D1的Tco + max数据链路延时+D2的Tsetup<T(T3<T-Tco-T2max)
2)D1的Tco + min数据链路延时>D2的Thold(T4<Tco+T2min)
实际中,某条数据链路的延时是一个定值,不过要求它在{T2min-T2max}之间
二、关于约束条件:
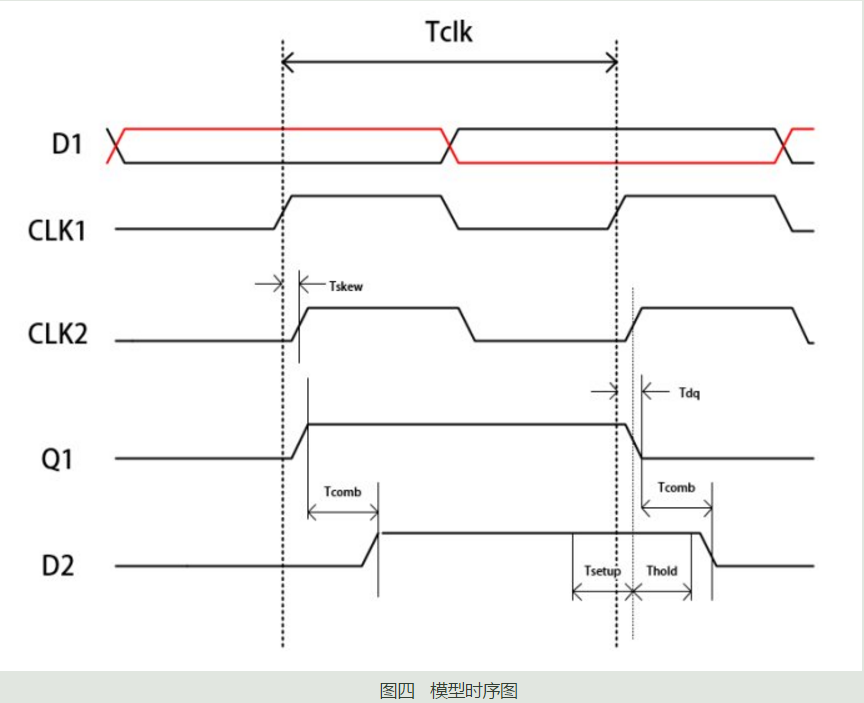
建立时间约束:
(1)式的思想其实就是在第二个时钟沿来临之前,数据稳定的时间一定要大于等于建立时间。因此在一个时钟周期内,数据稳定的时间为Tclk-Tdq-Tcomb,因为时钟也存在偏移,因此要把这个时钟偏移加上,于是最后数据稳定的时间为Tclk+Tskew-Tdq-Tcomb,满足这个稳定时间大于建立时间即可,因此推导出了(1)式,进而可以推导出在已知建立时间、组合逻辑延时、D触发器延时、时钟偏移的情况下,理论上能够承载的最大时钟频率为:
f_max = 1/(Tsetup+Tdq+Tcomb-Tskew)
这个关系式对于电路设计和芯片选型方面都有着非常大的帮助。当然,在实际工程中还要根据实际情况留有一定的设计余量以应对短暂的非常规情况。
保持时间约束:
(2)式的思想为在第二个时钟沿来临之后,数据稳定的时间一定要大于等于保持时间。因此在时钟沿来临之后,数据稳定的时间为Tdq+Tcomb,再减去时钟偏移则为Tdq+Tcomb-Tskew,满足这个稳定时间大于等于保持时间即可。
最后联立(1)(2)式我们可以推导得出:
组合逻辑延时范围:
Thold+Tskew-Tdq<=Tcomb<=Tclk-Tdq+Tkew-Tsetup
时钟偏移范围:
Tsetup-Tclk+Tdq+Tcomb<=Tskew<=Tdq+Tcomb-Thold
三、补充问题:
关于Tco大小分析:
与()有关呢,如何提高这部分的性能,对于组合逻辑呢,翻转的速度如何确定,如何提高?
假设数据是咋上升沿进行的采样,那么只需要保证数据在时钟上升沿到来前数据保持稳定,以及时钟上升沿后数据保持稳定,那么我们知道数据是在上升沿到来的那一瞬间被打入到触发器进而采样的,那么我们只要保证这一瞬间数据稳定不就行了么?理论上没啥问题,但实际上我们需要考虑D触发器的内部结构
图二是经典上升沿D触发器的内部结构图:
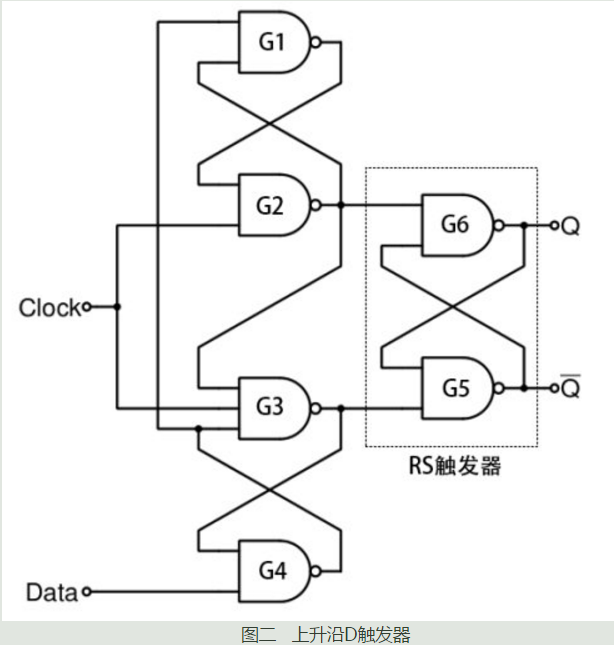
与非门G1到G4是维持阻塞电路,G5和G6构成一个RS触发器用于数据的锁存。如有不明白RS触发器的真值表和工作机理的可以在网上找到资料,这里不再累述。
图中可以看到,时钟信号直接作用在了G2和G3上面,也就意味着G2和G3是真正的采样传输门电路,输入信号应该要正确的被G2和G3采样后传输至后面的RS触发器。我们注意到,数据在传输到G3之前经过了G4,传输至G2之前经过了G4和G1。我们知道,实际情况中信号经过门电路是有延迟的。所以输入信号在到达G2和G3之前经过了G1和G4的延迟,因此就引入了建立时间的概念:建立时间就是为了补偿信号在G1和G4上的延迟。也就是数据在时钟沿来临之前,需要足够的建立时间让信号经过G1和G4到达G2和G3。触发器的建立时间主要取决于G1和G4.
那么保持时间呢?一样的,上升沿来临时,数据通过G2和G3传输至后面的RS触发器,但G2和G3也会存在延时。因此又引入了保持时间的概念:保持时间就是为了补偿信号在G2和G3上的延迟。也就是数据在时钟沿来临之后,需要足够的保持时间让信号正确的从G2和G3传输至RS触发器。触发器的保持时间主要取决于G2到G3,进而可以推断出,一般D触发器的保持时间比建立时间要长。
也许有人问,如果不满足建立时间和保持时间会怎样?很简单,因为在传输的过程中数据并不是处于稳定状态而处于亚稳态区,则会导致采样的数据可能会出错。
触发器可以将hold time减小到0
此外关于自己在SDC文件中的约束
setup violation
主要就是设法剪掉critical path的delay,要么pipeline(流水线分一下),要么retiming,要么把combination往前后级挪一挪。减小传输延时,降低时钟频率。
hold time violation
hold time violation是clock tree的skew引起的。主要的宗旨就是设法加前面一级combination的delay,比如加buffer什么的。这时候hold time不满足必须让前前面延迟大一些,并大到比clock period还大出至少一个hold time来。也可以适当把clock period缩小。不过hold time并不是自己能控制的,挺闹心的。或者可以减小时钟延时。
在综合时,综上所述,
setup violation是由于前级组合的延迟过大引起的,因此要用set_max_delay来限制,
hold violation是由于前级组合延迟过小引起的,因此不能让他太小,要用set_min_delay来限制。
再进一步分析下建立时间保持时间不满足发生的情况:
建立时间不满足是因为组合逻辑延时过于长,而保持时间不满足是因为逻辑团延时过小,建立时间保持时间都不满足发生在异步时钟域中一个讲的非常直观的PPT乍就没有早点看到这些东西,还是自己太懒了http://www.docin.com/p-977469569-f7.html