3665: maths
Description
Input
Output
Sample Input
2 2 2 2
Sample Output
HINT
对于100%的数据 T=2500 p<=10^12 n,M,A0,K<=10^18 p与A0互质 p与K互质
这道题很有趣。
由题,An=Kn * (An-1)m
即是→An=Kn * (Kn-1 * (An-2)m)m=Kn+(n-1)*m * (An-2m)m
这里需要注意 (An-2m)m≠An-2m*2,因为(An-2m)m=An-2m^2
大概还有An=Kn+(n-1)*m * (An-2)m^2=Kn+(n-1)*m * (Kn-2 * (An-3)m)m^2=Kn+(n-1)*m+(n-2)*m^2 * An-3m^3
这时候已经看的出了,An=Kn+(n-1)*m+(n-2)*m^2+……+(n-p+1)*m^(p-1) * An-pm^p
最后就是An=Kn+(n-1)*m+(n-2)*m^2+……+1*m^(n-1) * A0m^n了。
我们知道M,A0,K,n,要算出来已经不难了。A0m^n可以使用快速幂,再使用快速幂计算。但模数怎么取呢?
因为有欧拉定理:aφ(m)≡1(mod m),(a,m)=1。而A0与p互质,所以说mn的计算是可以%φ(p)的,之后计算A0m^n要%p。快速幂中要用快速乘,因为直接乘会爆long long。
同理,要算Kn+(n-1)*m+(n-2)*m^2+……+1*m^(n-1),应当算出n+(n-1)*m+(n-2)*m^2+……+1*m^(n-1)然后%φ(p),之后算Kn+(n-1)*m+(n-2)*m^2+……+1*m^(n-1)再%p。
但是怎么算n+(n-1)*m+(n-2)*m^2+……+1*m^(n-1)呢?嗯。设f[n]=n+(n-1)*m+(n-2)*m^2+……+1*m^(n-1),那么f[n-1]=n-1+(n-2)*m+……+1*m^(n-2),很明显f[n]=n+m*f[n-1]。这样的一个递推式确实没有通项啊。
怎么算呢?请看下图。
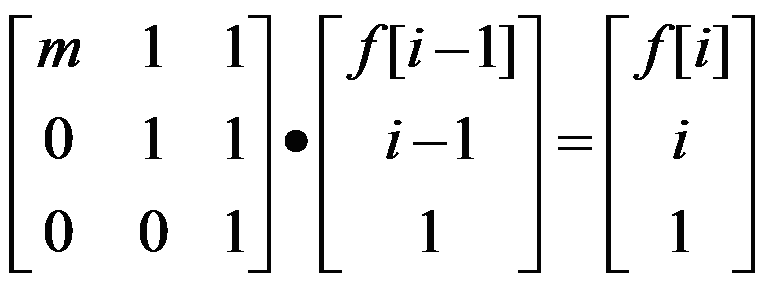
叠在一起,就是:
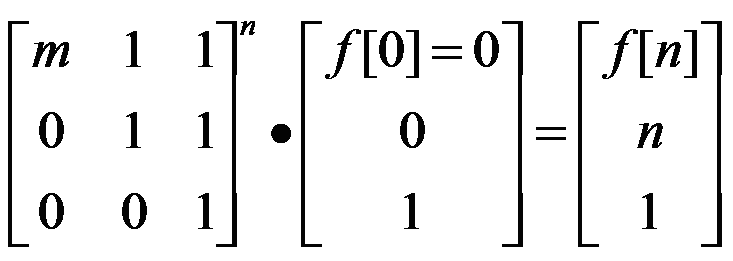
中间需要%PHI。
现在就说完了。准确上讲,这道题还是很好的,毕竟那些基础的板子大多都打了下来。像折半快速乘,快速幂,矩阵乘法,矩阵快速幂这几样递推神器都派上了大用场。而且,因为p比较大,所以需要在指数部时时%PHI,底下却是%P,在操作时需要多加小心(最开始TLE就是这个原因),做完之后也能更好的理解离散对数方面的内容。此外,题目并没有保证P是质数。幸好P不是10^18量级的数,还可以不用miller-rabin与pollard-rho这一系列的鬼畜东西(而这是BZOJ 4802 欧拉函数所需的)。
因为这题实在是太……我们为了卡常数,可以使用fread,也可以使用miller-rabin与pollard-rho。但是,最重要的一个就是快速乘。折半快速乘快得不是一点点。
代码如下:
1 /************************************************************** 2 Problem: 3665 3 User: Doggu 4 Language: C++ 5 Result: Accepted 6 Time:10688 ms 7 Memory:832 kb 8 ****************************************************************/ 9 10 #include <cstdio> 11 #include <cstring> 12 #include <algorithm> 13 #include <cmath> 14 struct MATRIX { 15 long long a[3][3]; 16 MATRIX() {memset(a,0,sizeof(a));} 17 }MAT; 18 long long MOD, PHI; 19 void getphi(long long p) { 20 PHI=p;long long bound = sqrt(p)+0.5; 21 for( int i = 2; i <= bound; i++ ) if(p%i==0) { 22 PHI=PHI/i*(i-1); 23 while(p%i==0) p/=i; 24 } 25 if(p>1) PHI=PHI/p*(p-1); 26 } 27 long long multify(long long a,long long b,long long mod) { long long ans=b/1000000*a%mod*1000000%mod+b%1000000*a%mod;return ans>mod?ans-mod:ans;} 28 long long mpow(long long a,long long b,long long mod) {long long ans=1;for(;b;b>>=1,a=multify(a,a,mod))if(b&1)ans=multify(ans,a,mod);return ans;} 29 MATRIX matrix_multify(MATRIX a,MATRIX b) { 30 MATRIX c; 31 for( int i = 0; i < 3; i++ ) for( int j = 0; j < 3; j++ ) for( int k = 0; k < 3; k++ ) c.a[i][j]+=multify(a.a[i][k],b.a[k][j],PHI), (c.a[i][j]>PHI)?c.a[i][j]-=PHI:1; 32 return c; 33 } 34 MATRIX matrix_mpow(MATRIX a,long long b) { 35 MATRIX ans; 36 for( int i = 0; i < 3; i++ ) ans.a[i][i]=1; 37 for(;b;b>>=1ll,a=matrix_multify(a,a)) if(b&1)ans=matrix_multify(ans,a); 38 return ans; 39 } 40 int main() { 41 int T;long long m, a0, k, n;scanf("%d%lld",&T,&MOD);getphi(MOD); 42 while(T--) { 43 scanf("%lld%lld%lld%lld",&m,&a0,&k,&n);m%=PHI;a0%=MOD;k%=MOD; 44 MAT.a[0][0]=m;MAT.a[0][1]=1;MAT.a[0][2]=1; 45 MAT.a[1][0]=0;MAT.a[1][1]=1;MAT.a[1][2]=1; 46 MAT.a[2][0]=0;MAT.a[2][1]=0;MAT.a[2][2]=1; 47 MAT=matrix_mpow(MAT,n); 48 printf("%lld ",multify(mpow(k,MAT.a[0][2],MOD),mpow(a0,mpow(m,n,PHI),MOD),MOD)); 49 } 50 return 0; 51 }